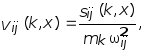4.Четвертый этап - внедрение в расчетную практику пространственных моделей зданий и сейсмических воздействий.

Рис. 1.10 Модели здания и его элементов

Как показали эксперименты, при горизонтальных колебаниях длинных зданий в их поперечном направлении перекрытия (особенно сборные) заметно деформируются в своей плоскости так, что ₁ становится сопоставимым с _2, показанным на рис. (1.10а) Обычно применяемое в расчетах допущение об абсолютной жесткости перекрытий в своей плоскости (₂=0) может привести к погрешностям, в частности к неточности распределения усилий между вертикальными элементами.

Простейшая трехмерная расчетная схема (модель) представлена на рис. (1.10б). Массы здания дискретно сосредоточены по высоте (в уровнях перекрытий) и равномерно по длине. Эту модель будем называть дискретно-континуальной. Воздействие инерционных сил на симметричную или несимметричную в плане систему при одновременном поступательном смещении основания всех ее опор y₀(t) может быть представлено силами, приложенными в уровнях перекрытий как показано на схеме 2 рис. 10. Если при этом пренебречь сопротивлением кручению перекрытий в вертикальной плоскости и всех вертикальных элементов в горизонтальной плоскости, то можно принять условия шарнирного опирания перекрытий на вертикальные конструкции здания и дальше рассматривать каждую плоскую конструкцию с упругими связями, имитирующими для рассматриваемого узла жесткости отброшенных элементов, как это показано на схемах 3-5 (рис. 1.10). Далее для упрощения решения вводится предположение (гипотеза) о подобии форм смещений каждой плоской конструкции : перекрытий и вертикальных элементов (диафрагм, каркасов и т.д.). Формы смещений называются подобными, если они отличаются постоянными множителями. Введение этого допущения позволяет выразить инерционные силы переносного движения (рис. 1.10) в виде сумм вспомогательных нагрузок, пропорциональных произведениям X_ik V_j(y) ординат форм собственных колебаний вертикальных элементов и перекрытий.

При указанном выше подходе пространственную систему можно расчленить на системы изолированных плоских элементов на поддерживающих и “толкающих” упругих опорах (рис. 1.10). Тогда составляющие сейсмической нагрузки, соответствующие i+j главным колебаниям пространственной системы, определяются по формуле:

(1.43)

где -приведенное ускорение грунта;

K_пр=K₁K₂..., -нормативные коэффициенты, учитывающие пластические и демпфирующие свойства здания, а также особенности его конструктивного решения;

(T_ij)- спектральный коэффициент динамичности (определяется по нормам);

T_ij- период собственных колебаний здания i+j тона;

(1.44)

X_ik,V_j(x) - ординаты форм собственных колебаний соответственно вертикальных и горизонтальных элементов здания;

n - число этажей.

Суммарная сейсмическая нагрузка, приходящаяся на k -этаж:

(1.45)

Если пространственная работа не проявляется, то V_j(x)=const , _j(x)=1,и мы приходим к формуле, принятой в нормах СССР и других стран для одномерной (консольной) модели зданий.²

Перемещения здания в уровне k-го перекрытия при сейсмическом воздействиях:

(1.46 )

где _ij=2/T_ij- частота собственных колебаний здания.

Сейсмические силы, приходящиеся на плоские элементы здания

(1.47)

где _id- частота собственных колебаний элемента, находящегося на расстоянии x_dот левого торца здания.

На рис. 1.11 показана зависимость сейсмических сил от длины здания с учетом и без учета пространственной работы ( для одной формы колебаний). Как видно из рис 1.11, при учете деформаций перекрытий в своей плоскости сейсмические нагрузки получаются в 2-3 раза меньшими, чем при определении по плоской (консольной) схеме, и есть оптимальная длина здания, которой соответствует минимальная сейсмическая нагрузка.

Указанные выше исследования проведены В. К. Егуповым и его сотрудниками еще в 1965 году и опубликованы в монографии [5] и учебнике [3].

Рис 1.11 График зависимости поэтажных сейсмических нагрузок от длины расчетной схемы.