Лабораторная работа № 16. Решение прямой геодезической задачи по методу Рунге – Кутта.

Формулы Рунге – Кутта основываются на методе численного интегрирования и используются для решения примой геодезической задачи с использованием вычислительной техники.

Исходные данные: B₁, L₁, A₁, s. Формулы, по которым производятся вычисления:

Пример решения прямой геодезической задачи по методу Рунге – Кутта.

B1	60° 00' 00"	k11	0,006646197	k31	0,00660719	B2	60° 22' 42,8586"
L1	10° 00' 00"	k12	0,013270039	k32	0,013423855	L2	10° 46' 08,8795"
A1	45° 00' 00"	k13	0,011492191	k33	0,011647511	A2	225° 40' 02,5027"
s	60000,000	k21	0,006607707	k41	0,006567959
M1	6383561,189	k22	0,013423277	k42	0,013579136
N1	6394315,136	k23	0,011647138	k43	0,01180448

Лабораторная работа №17. Решение обратной геодезической задачи на малые расстояния по формулам со средними аргументами.

По заданным координатам B₁, L₁, B₂, L₂ найти:

, ,,

, ,

С погрешностью на величины пятого порядка найти выражения:

,

,

.

Решение задачи завершается применением формул:

,

Знак	+	-	-	+
Знак	+	+	-	-

,

, .

Точность определения длины и азимута зависит от величины самой линии и характеризуется следующими предельными значениями погрешностей Δs и ΔА, соответствующими различным длинам определяемой линии s на всех широтах от 0 до 90^о:

s, км	Δs, км	ΔА"
80	0,01	0,02
200	0,1	0,1
400	1	0,5
600	5	1
800	10	2

Пример решения обратной геодезической задачи по способу со средним аргументом

B1	60° 00' 00"	Bm	60° 11' 21,4293"	а"	0° 40' 02,503"
L1	10° 00' 00"	Mm	6383745,136	Am	45° 20' 01,255"
B2	60° 22' 42,8586"	Nm	6394376,555	A1-2	45° 00' 00,003"
L2	10° 46' 08,8795"	l sin Bm	0,011647555	A2-1	225° 40' 02,506"
b	0° 22' 42,8586"	Q = s·cos Am	42178,607	S	60000,00393
l	0° 46' 08,8795"	P = s·sin Am	42672,774

Лабораторная работа №18. Редуцирование расстояний и направленний с элипсоида на плоскость.

Редуцирование расстояний с эллипсоида на плоскость.

Для перехода от длины геодезической линии на эллипсоиде к её длинена плоскости в проекции Гаусса-Крюгера применяется формула

где средний масштаб изображения.

Точность определения масштаба изображения зависит от длины линии и её удаления от осевого меридиана зоны, т.е. от величины средней ординаты концов линии,.

В геодезических сетях 1 класса длина линии на плоскости вычисляется до 0,001 м по формуле

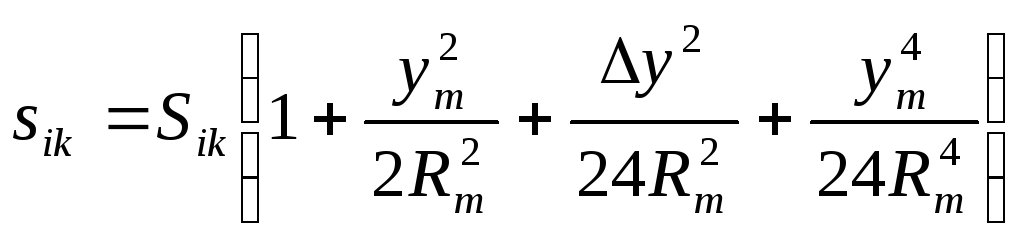
где ,средний радиус кривизны земного эллипсоида, выбирается по средней широте стороны.

В геодезических сетях 2 класса применяется более простая формула

В геодезических сетях низших классов достаточно ограничиться формулой

Для вычисления длин линий на плоскости в сетях 1, 2 и 3,4 классов необходимо знать ординаты соответственно с точностью 1м, 10 м и 0,1 км; ошибка в абсциссах не влияют на точность вычислений.

Вычисление поправок в горизонтальные направления за кривизну изображения геодезических линий на плоскости.

Поправки в прямое и обратноенаправления на пунктах триангуля-ции и полигонометрии 1 класса вычисляют до 0,001", при длинах сторон до 60 км применяют формулы

где .

В формуле () величины ивыражают в километрах, ординатыотсчитывают от осевого меридиана.

Для триангуляции и полигонометрии 2 – 4 классов формулы ( ) упрощаются и принимают вид

При км икм формулы могут быть использованы и в триангуляции 1 класса.

Формулы часто записывают в виде

При вычислении поправок с точностью порядка 0,1" можно пользоваться более простой формулой

.

Вычисленные поправки в горизонтальные направления за кривизну изображения геодезической линии на плоскости алгебраически прибавляются к значениям измеренных направлений.

Введением поправок в измеренные направления осуществляется переход от углов между криволинейными сторонами треугольника к углам между хордами, стягивающими концы этих сторон. Вследствие этого сумма углов в треугольнике уменьшается на величину его сферического избыткаε. Это обстоятельство используется в качестве контроля вычислений данных поправок: сумма поправок в углы А, В, С треугольника должна быть равна его сферическому избытку с обратным знаком, т.е.

где в углы находятся как разности поправок правогои левогонаправлений, образующих данный угол,.

Наиболее высокие требования к точности определения прямоугольных координат, необходимые для редукции расстояний и направлений на плоскость, предъявляются в триангуляции и полигонометрии 1 класса (1 – 2 м). Но вычисление координат с ошибками 1 – 2 м требует уже введения приближённых поправок ив длины сторон и направления, которые вычисляются по приближённым координатам. Таким образом, координаты и поправки для приведения триангуляции и полигонометрии 1 класса на плоскость находят последовательными приближениями.

Переход от геодезических азимутов к дирекционным углам.

Дирекционный угол хордысоединяющей точки 1 и 2 на плоскости при заданном азимутегеодезической линии на поверхности эллипсоида между этими точками, вычисляют по формуле

где гауссово сближение меридианов в точке 1;поправка за кривизну изображения геодезической линии, вычисляемая по формуле ( ) или ( ).

Для вычисления сближения меридианов в заданной точке можно использовать формулы (8.2), (8,3), (8,4). Для эллипсоида Красовского в триангуляции 1 класса, когда уголнадо знать до 0,001", сближение меридианов вычисляют по прямоугольным координатам по формуле

где

Если заданы геодезические координаты точки то используют формулу

где

Знак сближения меридианов совпадает со знаком разности долгот гдедолгота осевого меридиана зоны, долгота точки.