Граничные условия. Волновые уравнения.

Уравнения Максвелла в дифференциальной форме справедливы для сред, параметры которых не испытывают скачков в зависимости от координат. На практике встречаются случаи, когда рассматриваемая область состоит из разных сред. В этом случае надо исходить из уравнений Максвелла в интегральной форме.

Соотношения, показывающие связь между значениями векторов ЭМП в различных средах у поверхности раздела называются граничными условиями.

Граничные условия для векторов электрического поля.

Условия для нормальных составляющих векторов . Построим наS прямой цилиндр высотойh. Применим третье уравнение в интегральной форме:

где S_g – поверхность, а V – объем цилиндра.

S_g =  S₁+ S_бок+ S₂отсюда вытекает:

устремляем  h к 0.

В пределе S₁=S=S₂,- нормаль к поверхности.

При существовании поверхностного заряда.

Граничные условия показывают, что при переходе через поверхность раздела, несущую поверхностный заряд нормальной составляющей вектора претерпевает скачкообразные изменения. Причем величина скачка равна_S.Если _S=0, то D_1n=D_2n.

Условия для касательных составляющих векторов е и d.

- единичная касательная кl,- единичная нормаль к Р,образуют правовинтовую систему:

Применим второе уравнение Максвелла.

S – площадь, охватываемая ABCD, а .

Левая часть уравнения равна:

пусть h0 тогда

тогда

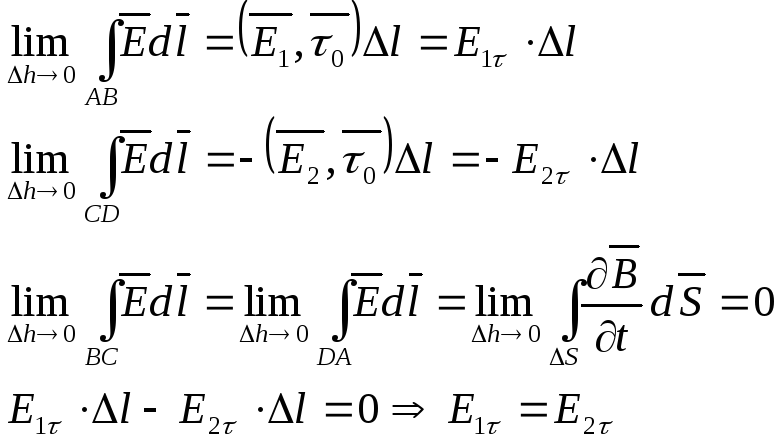
Касательная непрерывна при переходе через границу раздела двух сред. Касательнаяпретерпевает разрыв

Граничные условия для векторов магнитного поля.

Граничное условие для нормальной составляющей векторапроводится аналогично.

Запишем четвертое уравнение Максвелла в интегральной форме применительно к цилиндрическому объему, изображенному для вывода граничных условий для вектора .

Устремляя высоту цилиндра к нулю, получаем

В_1n= B_2n

Аналогично для выводим выражение

Граничные условия для касательной составляющей вектора выводится аналогично соотношению для вектора Е.

Применим первое уравнение Максвелла в интегральной форме к плоскому прямоугольному контуру ABCD

устремим h0

Если на границе отсутствуют поверхностные токи, то правая часть равенства равна нулю и

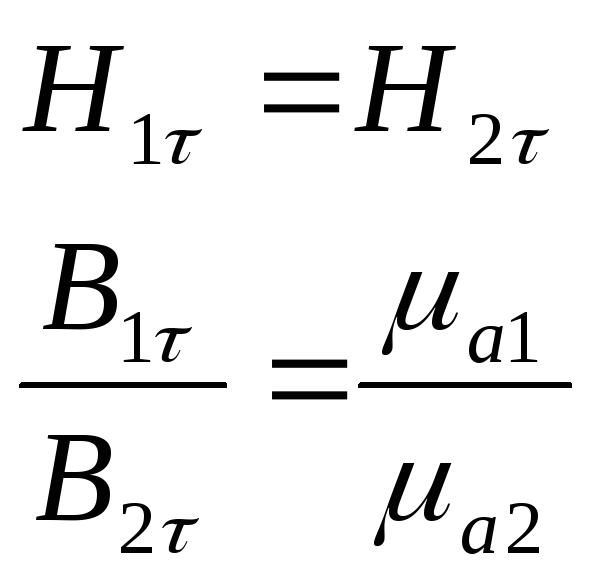
В случае наличия поверхностных токов

, где

j_SN– проекция векторана направляющий.

Граничные условия на поверхности проводящего тела.

Наиболее простой вид имеют граничные условия, если рассматриваемое материальное тело считать идеально проводимым . Как известно в сверхпроводнике поле отсутствует

, тогда:

.

Приближенные граничные условия для ЭМП, справедливые для случая, когда одну из сред можно считать хорошимпроводником, получены академиком Леонтовичем: в этом случае ЭМП, падающая под произвольным угломна границы раздела входит внутрь среды 2 приближенно по нормали. В соответствии с этим эквивалентная схема проводимости среды будет иметь вид однородной линии с характеристикой сопротивления, тогда в начале линии, что соответствует границе раздела, тангенциальную составляющую Н и Е удовлетворяет соотношению, вытекающему из определенных характеристик сопротивления. Составляющие векторов в первой среде связано между собой через параметры второй среды.

Волновые уравнения.

Из уравнений Максвелла следует, что изменение во времени приводит к возникновениюи наоборот. Аналогичные явления происходят в колебательном контуре. Такое явление в физике носит названиеволнового процесса.

Уравнения Максвелла можно преобразовать в уравнения, которые описывают волновой процесс и носят название волновых.

Оператор Гамильтона (набла – оператор).

-оператор Лапласа (лапласиан)

Возьмем ротор от обеих частей первого уравнения Максвелла и изменим порядок дифференцирования по времени и координатам. С учетом получим:

Левая часть:

, т.к.то. Учитывая, что из второго уравнения, перепишем уравнениев форме:

если, то правая часть равна нулю.

Это уравнение относится к уравнениям типа:

Такие уравнения описывают волновые процессы, причем параметр V равен скорости этого процесса.