1) Підставимо в канонічне рівняння еліпса 4078 замість такоординати точкиА, а також дане значення . Одержимо рівняння:.

Розв’яжемо його:

Отже, відповідь:

.

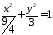1. З умови задачі маємо:

, отже, .

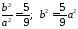З другого боку, підставимо у канонічне рівняння координати точки А. Одержимо систему рівнянь:

.

Звідси

,

отже шукане рівняння має вигляд:

.

Задача 43.2. Скласти рівняння гіперболи, фокуси якої розташовані на осі абсцис симетрично щодо початку координат, якщо відомі:

1) – рівняння асимптот,– відстань між вершинами;

2) – точки на гіперболі.

Розв’язання.

1) Канонічне рівняння гіперболи має вигляд 4187, де .

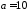Оскільки рівняння асимптот задаються формулами 4190, з умови задачі одержимо:

.

Отже відповідь:

.

2) Підставимо координати обох точок у рівняння гіперболи. Одержимо систему рівнянь

В результаті заміни

система зведеться до системи лінійних рівнянь

,

яку можна розв’язати за правилом Крамера. Обчислимо визначники:

Тоді

,

Тобто

.

Отже, відповідь: .

Задача 43.3. Скласти рівняння параболи, вершина якої знаходиться у початку координат, якщо відомо:

1) парабола симетрична відносно осі та проходить через точку;

2) – фокус параболи.

Розв’язання.

1) Канонічне рівняння параболи має вигляд .

Підставимо у це рівняння координати точки А. Маємо . Отже відповідь:.

2) Оскільки координати фокуса задаються формулою , то. Отже відповідь:.

Задача 43.4. Записати рівняння еліпса, фокуси якого розташовані на осі симетрично відносно початку координат, точканалежить еліпсу, а відстань між директрисами дорівнює 10.

Розв’язання.

Оскільки точка належить еліпсу, то її координати здовольняють рівняння 4078:

, або .

Відстань між директрисами 4082 дорівнює

, звідки .

Отримали систему рівнянь

розв’язки якої

.

Отже,

,

і шукане рівняння еліпса набуває вигляду:

.

Задача 43.5. На правій гілці гіперболи знайти точку, відстань від якої до правого фокуса в два рази менша від відстані до лівого фокуса.

Розв’язання.

Для правої гілки гіперболи фокальні радіуси 4192 визначаються за формулами

.

Отже, за умовою задачі маємо рівняння

,

звідки

.

З канонічного рівняння гіперболи маємо, що , тодіі. Тобто.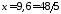

Ординату шуканої точки знайдемо з рівняння гіперболи:

.

Таким чином, умові задачі задовольняють дві точки: .

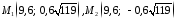Задачі для самостійної роботи

1. Гіпербола, симетрична відносно осей координат, проходить через точки . Записати її канонічне рівняння та побудувати гіперболу.

2. Скласти канонічне рівняння, побудувати параболу та її фокус, якщо відомо рівняння директриси: .

3. На гіперболі взято точку з ординатою, рівною 1. Знайти відстані від цієї точки до фокусів.

4. Еліпс, симетричний відносно осей координат, проходить через точку та має ексцентриситет . Записати його канонічне рівняння.

5. Знайти рівняння і побудувати гіперболу, фокуси якої розташовані на осі абсцис симетрично відносно початку координат, якщо відстань між її директрисами дорівнює , а ексцентриситет.

6. Кут між асимптотами гіперболи дорівнює . Обчислити її ексцентриситет.

7. Ордината точки на параболі дорівнює5. Знайти відстань від цієї точки до фокуса. Побудувати параболу, її фокус і директрису.

8. На параболі знайти точку, відстань до якої від директриси дорівнює 4.

9. Скласти рівняння і побудувати еліпс, симетричний відносно осей координат, якщо йому належить точка і відстань між фокусами дорівнює8.

10. Скласти рівняння і побудувати гіперболу, якщо її ексцентриситет , а фокуси співпадають з фокусами еліпса.