
- •Розділ II. Елементи аналітичної геометрії
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •1) Підставимо в канонічне рівняння еліпса 4078 замість такоординати точкиА, а також дане значення . Одержимо рівняння:.
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •§ 48. Розв’язування задач на складання рівнянь поверхонь та їх дослідження
- •Задачі для самостійної роботи
- •Питання для повторення
- •Відповіді
- •Додаток
- •Програма модульного контролю з теми
- •Лінійна і векторна алгебра
- •Теоретичні запитання.
- •Зразки практичних завданнь.
- •Програма модульного контролю з теми аналітична геометрія Теоретичні запитання.
- •Зразки практичних завдань.
- •Література.
Задачі для самостійної роботи
Скласти рівняння прямої, що проходить через точку
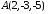 перпендикулярно до площини
перпендикулярно до площини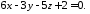
Скласти рівняння площини, яка проходить через точку
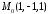 перпендикулярно прямій
перпендикулярно прямій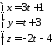
Знайти кут між прямою
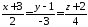 та площиною
та площиною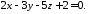
Знайти точку перетину прямої
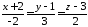 та площини
та площини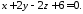
Скласти рівняння площини, яка проходить через пряму
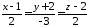 перпендикулярно площині
перпендикулярно площині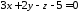 .
.Скласти рівняння площини, що проходить через пряму
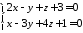 паралельно
вектору
паралельно
вектору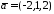 .
.Перевірити паралельність прямої
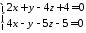 та
площини
та
площини
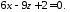
Питання для повторення
Кут між прямою і площиною.
Умови паралельності та перпендикулярності прямої та площини.
Знаходження точки перетину прямої та площини.
4836Equation Section (Next)§36. Загальне і параметричне рівняння лінії на координатній площині. Рівняння кола. Загальне рівняння прямої на площині
Будь
яка ліня
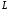 ,
що знаходиться у площині
,
що знаходиться у площині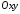 ,може
бути утворена як перетин деякої поверхні,
заданої рівнянням
,може
бути утворена як перетин деякої поверхні,
заданої рівнянням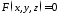 ,
і площини
,
і площини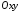 (Рис. 36.1)
(Рис. 36.1)
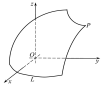
Рис. 36.1
Тоді
кожна точка лінії
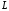 задовольняє систему рівнянь
задовольняє систему рівнянь
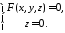 493649\* MERGEFORMAT (.)
493649\* MERGEFORMAT (.)
Можна
у перше рівняння підставити
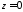 і перепозначити
і перепозначити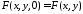 .
Тоді 3649 набуває вигляду
.
Тоді 3649 набуває вигляду
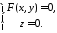 503650\* MERGEFORMAT (.)
503650\* MERGEFORMAT (.)
Це
загальне рівняння лінії, що належить
площині
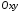 ,
записане у тривимірній системі координат
,
записане у тривимірній системі координат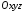 .
Якщо розглядати двовимірну систему
координат
.
Якщо розглядати двовимірну систему
координат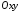 ,
то загальне рівняння лінії виглядає
наступним чином:
,
то загальне рівняння лінії виглядає
наступним чином:
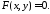 513651\* MERGEFORMAT (.)
513651\* MERGEFORMAT (.)
Параметричне
рівняння лінії, що належить площині
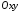 ,
згідно 265 подається так:
,
згідно 265 подається так:
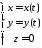 ,
,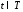 або
або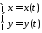 ,
,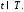 523652\* MERGEFORMAT (.)
523652\* MERGEFORMAT (.)
Отримаємо
рівняння кола радіус
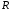 ,
центр якого співпадає з точкою площини
,
центр якого співпадає з точкою площини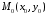 .
.
Для
цього у тривимірній системі координат
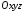 візьмемо сферу у цій самій точці. Вона
визначається наступним рівнянням
візьмемо сферу у цій самій точці. Вона
визначається наступним рівнянням
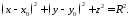
Коло
утворюється як перетин цієї сфери з
площиною
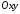 (Рис. 36.2).
(Рис. 36.2).
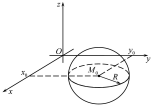
Рис. 36.2
Воно визначається системою рівнянь
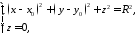
яка еквівалентна одному наступному рівнянню вигляду 3651
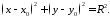 533653\* MERGEFORMAT (.)
533653\* MERGEFORMAT (.)
Рівняння
3653 і є рівнянням
кола
на координатній площині
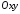 з центром у точці
з центром у точці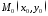 і радіуса
і радіуса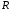 .
.
Пряма
на координатній площині
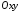 може бути утворена перетином цієї
площини з довільною площиною (Рис. 36.3),
яка задана загальним рівнянням
може бути утворена перетином цієї
площини з довільною площиною (Рис. 36.3),
яка задана загальним рівнянням
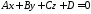 . 543654\* MERGEFORMAT (.)
. 543654\* MERGEFORMAT (.)
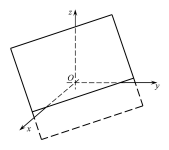
Рис. 36.3
Причому
у рівнянні 3654 хоча б один з коефіцієнтів
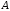 чи
чи
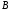 має
бути відмінним від
має
бути відмінним від
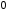
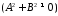 .
Інакше площини
.
Інакше площини
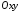 і 3654 будуть паралельними і не перетинатися.
Тоді пряма, що утворюється внаслідок
перетину, визначається системою рівнянь
і 3654 будуть паралельними і не перетинатися.
Тоді пряма, що утворюється внаслідок
перетину, визначається системою рівнянь
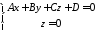 ,
,
або
одним рівнянням:
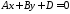 .
.
Для зручності в останньому рівнянні перепозначимо коефіцієнти і запишемо його у вигляді:
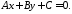 553655\* MERGEFORMAT (.)
553655\* MERGEFORMAT (.)
Має місце теорема:
Теорема.
Будь-яке рівняння
3655
визначає на координатній площині пряму,
перпендикулярну до вектора
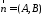 .
.
Дійсно,
оскільки
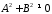 ,
то
рівняння 3655 має хоча б один розв’язок.
Нехай
,
то
рівняння 3655 має хоча б один розв’язок.
Нехай
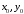 - будь-який
розв’язок цього рівняння. Тоді є вірною
рівність
- будь-який
розв’язок цього рівняння. Тоді є вірною
рівність
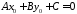 . 563656\* MERGEFORMAT (.)
. 563656\* MERGEFORMAT (.)
Складемо різницю рівнянь 3655 і 3656
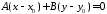 573657\* MERGEFORMAT (.)
573657\* MERGEFORMAT (.)
Розглянемо
точки
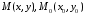 і вектор
і вектор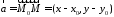 .
Рівняння 3657 можна записати у вигляді
.
Рівняння 3657 можна записати у вигляді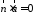 .
Це
означає, що усі вектори
.
Це
означає, що усі вектори
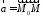 мають початок у точці
мають початок у точці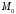 і перпендикулярні до вектора
і перпендикулярні до вектора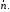 ,
тобто
знаходяться на одній
прямій,
що
перпендикулярна до цього вектора. Саме
цю пряму визначає рівняння 3656.
,
тобто
знаходяться на одній
прямій,
що
перпендикулярна до цього вектора. Саме
цю пряму визначає рівняння 3656.
Рівняння
3656 називається загальним
рівнянням прямої
на координатній площині. Якщо розглянути
довільні
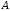 і
і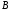 ,
то це рівняння визначає усі прямі, що
проходять через точку
,
то це рівняння визначає усі прямі, що
проходять через точку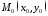 і називається рівнянням пучка прямих,
що проходять через задану точку.
і називається рівнянням пучка прямих,
що проходять через задану точку.
5837Equation Section (Next)§37. Різні види рівняння прямої на координатній площині
Рівняння прямої у відрізках на осях.
Якщо
знайти пряму, що утворюється перетином
площини, заданої рівнянням 2815 у відрізках
на координатних осях, і координатної
площини
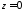 ,
то вона визначатиметься рівнянням
,
то вона визначатиметься рівнянням
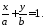 593759\* MERGEFORMAT (.)
593759\* MERGEFORMAT (.)
Пряма,
що задається рівнянням 3759, перетинає
осі
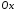 та
та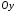 у точках
у точках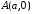 і
і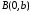 (Рис. 37.1)
(Рис. 37.1)
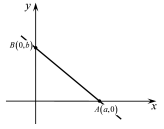
Рис. 37.1
і
відтинає на них відрізки довжиною
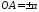 ,
,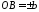 .
Рівняння 3759 називається рівнянням
прямої у відрізках на координатних
осях.
.
Рівняння 3759 називається рівнянням
прямої у відрізках на координатних
осях.
Канонічне і параметричне рівняння прямої на площині.
Нехай
є ненульовий вектор
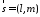 і точка
і точка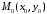 ,
тоді рівняння прямої, що проходить через
дану точку паралельно вектору згідно
3127,
має вигляд:
,
тоді рівняння прямої, що проходить через
дану точку паралельно вектору згідно
3127,
має вигляд:
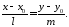 603760\* MERGEFORMAT (.)
603760\* MERGEFORMAT (.)
Це канонічне рівняння прямої на площині.
Параметричне
рівняння отримується з
3129
відкиданням третього рівняння, яке
перетворюється у тотожність вигляду
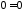 :
:
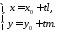 613761\* MERGEFORMAT (.)
613761\* MERGEFORMAT (.)
Рівняння прямої, що проходить через дві точки.
Рівняння
прямої, що проходить через дві задані
точки площини
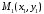 і
і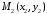 ,
складається аналогічно просторовому
випадку
3130:
,
складається аналогічно просторовому
випадку
3130:
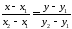 . 623762\* MERGEFORMAT (.)
. 623762\* MERGEFORMAT (.)
Рівняння прямої з кутовим коефіцієнтом.
Нехай
пряма, що проходить через точку
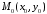 ,
задана рівнянням 3657 і утворює з віссю
,
задана рівнянням 3657 і утворює з віссю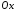 кут
кут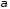 (Рис. 37.2). Тоді нормальний вектор цієї
прямої
(Рис. 37.2). Тоді нормальний вектор цієї
прямої
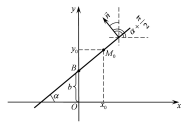
Рис. 37.2
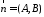 утворює
з осями координат кути
утворює
з осями координат кути
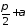 і
і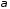 і для його координат виконується
рівність
і для його координат виконується
рівність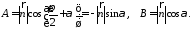
За допомогою останніх формул з 3657 знаходимо
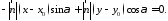
Оскільки
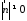 ,
ділимо обидві частини на
,
ділимо обидві частини на
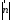
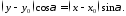
Нехай
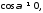 тобто
пряма не паралельна осі
тобто
пряма не паралельна осі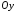 .
Введемо позначення
.
Введемо позначення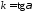 .
Тоді останнє рівняння перепишеться у
вигляді
.
Тоді останнє рівняння перепишеться у
вигляді
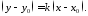 633763\* MERGEFORMAT (.)
633763\* MERGEFORMAT (.)
Число
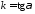 ,
яке дорівнює тангенсу кута, утвореного
прямою з додатним напрямом осі
,
яке дорівнює тангенсу кута, утвореного
прямою з додатним напрямом осі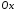 ,
називається кутовим коефіцієнтом
прямої.
,
називається кутовим коефіцієнтом
прямої.
Якщо
вважати
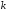 довільним, то рівняння 3763 визначає
пучок прямих, що проходять через точку
довільним, то рівняння 3763 визначає
пучок прямих, що проходять через точку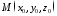 ,
за виключенням прямої
,
за виключенням прямої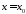 ,
паралельної до осі
,
паралельної до осі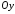 .
.
Здійснимо за рівнянням (9.5) наступні перетворення
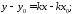
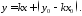
і
введемо позначення
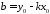 .
Знайдемо
рівняння
.
Знайдемо
рівняння
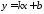 643764\* MERGEFORMAT (.)
643764\* MERGEFORMAT (.)
де
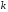 -кутовий
коефіціент прямої,
-кутовий
коефіціент прямої,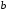 -
координата точки
-
координата точки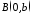 перетину прямої з віссю
перетину прямої з віссю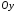 .
Рівняння 3764 називається рівнянням
прямої з кутовим коефіціентом.
.
Рівняння 3764 називається рівнянням
прямої з кутовим коефіціентом.
6538Equation Section (Next)§38. Обчислення відстані від точки до прямої і кута між двома прямими на координатній площині
Розглянемо
на координатній площині
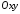 пряму, задану загальним рівнянням
пряму, задану загальним рівнянням
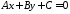 663866\* MERGEFORMAT (.)
663866\* MERGEFORMAT (.)
і
точку
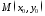 поза
цією прямою.
поза
цією прямою.
Рівняння
3866 у відповідній тривимірній системі
координат
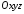 визначає площину, паралельну до осі
визначає площину, паралельну до осі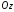 з нормальним вектором
з нормальним вектором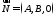 .
(Рис. 38.1).
.
(Рис. 38.1).
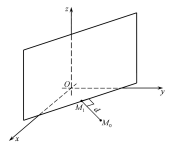
Рис. 38.1
Проведемо
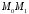 - перпедикуляр до прямої. Тоді
- перпедикуляр до прямої. Тоді
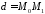 -
це відстань як до прямої у системі
-
це відстань як до прямої у системі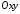 ,
так і до площини у системі
,
так і до площини у системі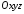 .
Тоді за формулою 2819 після покладення
.
Тоді за формулою 2819 після покладення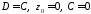 ,
знаходимо
,
знаходимо
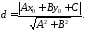 673867\* MERGEFORMAT (.)
673867\* MERGEFORMAT (.)
Обчислення
кута між прямими на координатній площині
здійснюється в залежності від того,
якими рівняннями вони задані. При
задаванні прямих загальним рівнянням
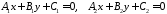 кут між
прямими визначається як кут
кут між
прямими визначається як кут
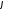 між їх нормальними векторами
між їх нормальними векторами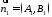 і
і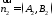 і обчислюється за формулою аналогічно
до 2922:
і обчислюється за формулою аналогічно
до 2922:
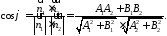 683868\* MERGEFORMAT (.)
683868\* MERGEFORMAT (.)
У випадку завдання прямих канонічними рівняннями
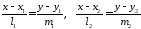
кут
між прямими визначається як кут
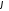 між їх напрямними векторами
між їх напрямними векторами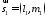 і
і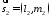 і обчислюється згідно формули 3239:
і обчислюється згідно формули 3239:
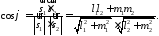 693869\* MERGEFORMAT (.)
693869\* MERGEFORMAT (.)
Розглянемо випадок, коли прямі задано рівняннями з кутовим коефіціентами:
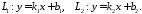 703870\* MERGEFORMAT (.)
703870\* MERGEFORMAT (.)
Нехай
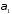 і
і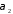 кути, утворені цими прямими з додатним
напрямком осі
кути, утворені цими прямими з додатним
напрямком осі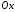 (Рис. 38.2):
(Рис. 38.2):
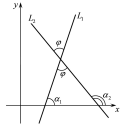
Рис. 38.2
Тоді
за властивостю зовнішнього кута
трикутника
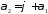 ,
або
,
або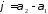 .
.
Тоді
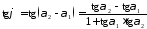 ,
або оскільки
,
або оскільки
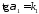 ,
,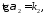
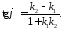 713871\* MERGEFORMAT (.)
713871\* MERGEFORMAT (.)
Оскільки
паралельні прямі нахилені до осі
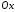 під однаковим кутом, то умовою паралельності
прямих 3870 є рівність
під однаковим кутом, то умовою паралельності
прямих 3870 є рівність
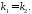 723872\* MERGEFORMAT (.)
723872\* MERGEFORMAT (.)
Якщо
прямі 3870 перпендикулярні, то
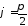 і тангенс кута
і тангенс кута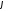 є нескінченно великою величиною. Тому
умова перпендикулярності цих прямих
має вигляд:
є нескінченно великою величиною. Тому
умова перпендикулярності цих прямих
має вигляд:
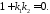 733873\* MERGEFORMAT (.)
733873\* MERGEFORMAT (.)
7439Equation Section (Next)§ 39. Пряма на координатній площині. Приклади розв’язування задач
Задача
39.1.
Визначити, які з точок
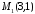 та
та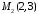 лежать на прямій
лежать на прямій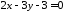 ,
а які не лежать на ній.
,
а які не лежать на ній.
Розв’язання.
Точка
лежить на прямій тоді і тільки тоді,
коли її координати задовольняють
рівняння прямої. Підставимо координати
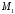 в рівняння прямої. Одержимо
в рівняння прямої. Одержимо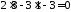 ,
значить ця точка лежить на прямій.
,
значить ця точка лежить на прямій.
Тепер
підставимо координати
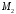 :
: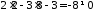 ,
значить
,
значить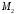 прямій не належить.
прямій не належить.
Задача
39.2.
Визначити точки перетину прямої
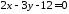 з координатними осями та накреслити цю
пряму.
з координатними осями та накреслити цю
пряму.
Розв’язання.
На
осі
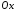
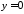 ,
тому
,
тому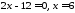 ,
значить точкою перетину з віссю
,
значить точкою перетину з віссю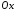 є
є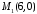 .
.
На
осі
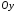
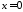 ,
тому
,
тому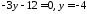 ,
значить точкою перетину з
,
значить точкою перетину з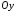 є
є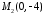 .
.
Для побудови прямої зобразимо ці точки на координатній площині та проведемо через них пряму (Рис. 39.1).
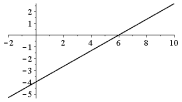
Рис.39.1
Задача
39.3.
Знайти точку перетину двох прямих
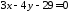 та
та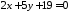 .
.
Розв’язання.
Координати
точки перетину двох прямих повинні
задовольняти двом рівнянням прямих
одночасно, тому для знаходження точки
перетину розв’яжемо систему
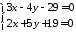 .
.
Маємо
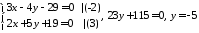 .
.
Значить,
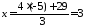 ,
тобто точка перетину
,
тобто точка перетину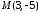 .
.
Задача
39.4.
Дано
вектор
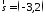 .
Записати загальне, канонічне, параметричне
та з кутовим коефіцієнтом рівняння
прямої, що проходить через точку
.
Записати загальне, канонічне, параметричне
та з кутовим коефіцієнтом рівняння
прямої, що проходить через точку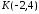 паралельно
паралельно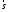 .
.
Розв’язання.
Згідно 3760 канонічне рівняння має вигляд:
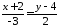 ,
,
параметричне з 3761
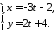
Загальне рівняння отримаємо з канонічного. За властивістю пропорції
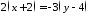 ,
тобто
,
тобто
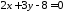 .
.
Останнє рівняння виду 3866 є загальним рівнянням даної прямої.
Щоб
отримати рівняння прямої з кутовим
коефіцієнтом 3764, достатньо з загального
виразити
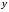 :
:
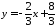 .
.
Задача
39.5.
Дана пряма l:
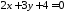 .
Скласти рівняння прямої, що проходить
через точку
.
Скласти рівняння прямої, що проходить
через точку
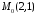
1) перпендикулярно до даної прямої;
2) паралельно даній прямій.
Розв’язання.
1)
Позначимо шукану пряму l1.
Нормальний
вектор до заданої прямої l
можна знайти з її рівняння. Це вектор
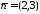 .
Для шуканої прямоїl1
цей
вектор є напрямним, тому для того, щоб
записати її рівняння можна використати
канонічне рівняння прямої 3760:
.
Для шуканої прямоїl1
цей
вектор є напрямним, тому для того, щоб
записати її рівняння можна використати
канонічне рівняння прямої 3760:
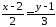 .
.
2
спосіб:
Кутовий коефіцієнт прямої l
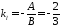 ,
тоді
з умови перпендикулярності
прямих
3873
,
тоді
з умови перпендикулярності
прямих
3873
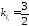 .
.
Використавши рівняння пучка прямих 3763, отримаємо:
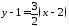 ,
або
,
або
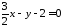 .
.
2)
Позначимо шукану пряму l2.
Нормальний
вектор
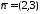 заданої прямоїl
є нормальним і для шуканої прямої l2.
Тому, щоб записати рівняння цієї прямої,
ми можемо скористатися формулою 3657:
заданої прямоїl
є нормальним і для шуканої прямої l2.
Тому, щоб записати рівняння цієї прямої,
ми можемо скористатися формулою 3657:
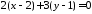 ,
або
,
або
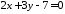 .
.
2
спосіб:
Кутовий коефіцієнт прямої l
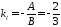 ,
тоді
з умови паралельності
прямих
3872
,
тоді
з умови паралельності
прямих
3872
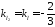 .Використавши
рівняння
пучка
прямих 3763, отримаємо:
.Використавши
рівняння
пучка
прямих 3763, отримаємо:
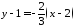 ,
або
,
або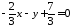 .
.
Задача
39.6.
Дано вершини трикутника
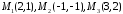 .
Скласти рівняння:
.
Скласти рівняння:
1)
висоти
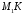 ;
;
2)
сторони
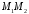 ;
;
3)
медіани
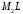 ;
;
4)
перпендикуляра
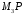 опущеного з вершини
опущеного з вершини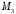 на медіану
на медіану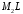 .
.
Розв’язання.
Зробимо креслення.
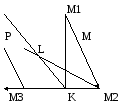
Рис. 39.2
1)
Нормальним вектором для висоти
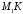 (Рис. 39.2) є вектор
(Рис. 39.2) є вектор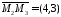 .
Так як пряма
.
Так як пряма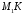 проходить через точку
проходить через точку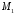 ,
одержимо рівняння цієї прямої:
,
одержимо рівняння цієї прямої: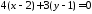 ,
або
,
або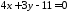 .
.
2)
Напрямним вектором для сторони
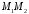 є вектор
є вектор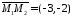 .
Тоді канонічне рівняння цієї прямої
набуде вигляду
.
Тоді канонічне рівняння цієї прямої
набуде вигляду
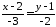 .
.
Знайдемо координати точки
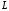 ,
використовуючи формулу для знаходження
координат середини відрізку. Маємо
,
використовуючи формулу для знаходження
координат середини відрізку. Маємо
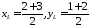 ,
тобто
,
тобто
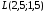 .
.
Напрямний вектор медіани – це вектор
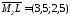 .
Тоді канонічне рівняння медіани:
.
Тоді канонічне рівняння медіани: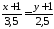 .
.Вектор
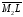 є нормальним для
є нормальним для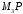 ,
тому рівняння цього перпендикуляра
може бути записано у вигляді
,
тому рівняння цього перпендикуляра
може бути записано у вигляді
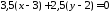 ,
,
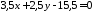 або
або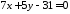 .
.
Задача
39.7.
Знайти
проекцію точки
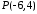 на пряму
на пряму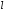 :
: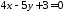 .
.
Розв’язання.
Накреслимо рисунок.

Рис. 39.3
Спочатку
складемо рівняння прямої
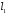 ,
яка проходить через точку
,
яка проходить через точку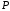 перпендикулярно даній прямій (Рис.39.3).
Нормальним вектором для даної прямої
є вектор
перпендикулярно даній прямій (Рис.39.3).
Нормальним вектором для даної прямої
є вектор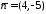 ,
і цей вектор є напрямним для прямої
,
і цей вектор є напрямним для прямої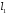 .
Тому канонічне рівняння прямої
.
Тому канонічне рівняння прямої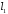 :
:
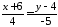 .
.
В результаті перетворень це рівняння набуде вигляду.
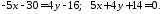
Шукана
точка М
є точкою перетину
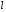 та
та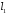 ,
тому її координати знайдемо, розв’язавши
систему:
,
тому її координати знайдемо, розв’язавши
систему:
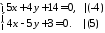 .
.
Маємо
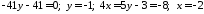 .
.
Отже,
координати точки
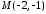 .
.
Задача
39.8.
Дано
рівняння двох сторін прямокутника
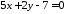 ,
,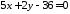 та рівняння його діагоналі
та рівняння його діагоналі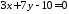 .
Скласти рівняння інших двох сторін
цього прямокутника.
.
Скласти рівняння інших двох сторін
цього прямокутника.
Розв’язання.
Відразу помітимо, що дві задані прямі
паралельні, оскільки мають однакові
нормальні вектори, тому представляють
протилежні сторони прямокутника,
наприклад
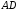 і
і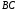 .
.
Точка
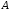 є точкою перетину
є точкою перетину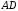 і діагоналі
і діагоналі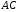 ,
тому знайдемо її координати, розв’язавши
систему рівнянь.
,
тому знайдемо її координати, розв’язавши
систему рівнянь.
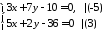
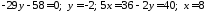 ,
тобто
,
тобто
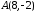 .
.
Аналогічно
знайдемо точку
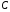 ,
як точку перетину
,
як точку перетину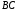 та діагоналі
та діагоналі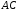 .
.
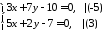
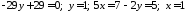 ,
тобто
,
тобто
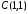 .
.
Нормальним
вектором для
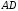 і
і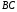 є вектор
є вектор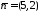 .
Цей вектор є напрямним для
.
Цей вектор є напрямним для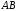 і
і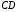 .
Тому рівняння цих сторін такі:
.
Тому рівняння цих сторін такі:
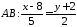 ;
;
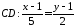
Задача
39.9.
Знайти
кут між прямими
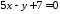 та
та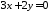 .
.
Розв’язання.
Нормальні
вектори цих прямих мають координати
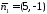 і
і відповідно. Кут між прямими дорівнює
куту між нормальними векторами, а косинус
кута між векторами може бути знайдений
за формулою 3869, тобто
відповідно. Кут між прямими дорівнює
куту між нормальними векторами, а косинус
кута між векторами може бути знайдений
за формулою 3869, тобто
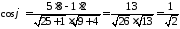 .
.
Отже,
кут між прямими
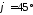 .
.
Задача
39.10.
Визначити,
при якому значенні
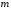 дві прямі
дві прямі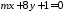 ,
,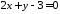 паралельні та перпендикулярні.
паралельні та перпендикулярні.
Розв’язання.
Нормальні
вектори для цих прямих мають координати
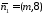 і
і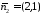 відповідно.
відповідно.
Дві прямі перпендикулярні, коли їх нормальні вектори ортогональні , тобто скалярний добуток цих векторів має дорівнювати нулю. Обчислимо скалярний добуток:
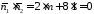 .
.
З
цього рівняння
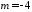 .
.
Дві прямі паралельні, коли їх нормальні вектори колінеарні. Умовою колінеарності векторів є пропорційність їх координат. Запишемо цю умову для наших нормальних векторів:
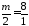 ,
значить
,
значить
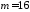 .
.
Задача
39.11.
Знайти
відстань між двома паралельними прямими
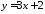 та
та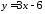 .
.
Розв’язання.
Зобразимо рисунок.
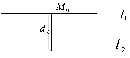
Рис. 39.4
Знайдемо
одну точку на прямій
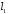 .
Для цього в її рівняння підставимо,
наприклад,
.
Для цього в її рівняння підставимо,
наприклад,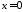 .
Одержимо
.
Одержимо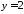 ,
тобто точка на прямій
,
тобто точка на прямій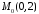 .
Перетворимо рівняння другої прямої,
перенісши всі доданки в ліву частину
рівності:
.
Перетворимо рівняння другої прямої,
перенісши всі доданки в ліву частину
рівності:
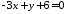 .
.
Відстань
між двома прямими – це відстань від
точки
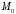 до прямої
до прямої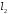 .
(Рис. 39.4). Відстань від точки
.
(Рис. 39.4). Відстань від точки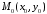 до прямої
до прямої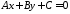 обчислюється за формулою 3867.
обчислюється за формулою 3867.
В нашому випадку
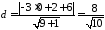 .
.
