
- •Розділ II. Елементи аналітичної геометрії
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •1) Підставимо в канонічне рівняння еліпса 4078 замість такоординати точкиА, а також дане значення . Одержимо рівняння:.
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •§ 48. Розв’язування задач на складання рівнянь поверхонь та їх дослідження
- •Задачі для самостійної роботи
- •Питання для повторення
- •Відповіді
- •Додаток
- •Програма модульного контролю з теми
- •Лінійна і векторна алгебра
- •Теоретичні запитання.
- •Зразки практичних завданнь.
- •Програма модульного контролю з теми аналітична геометрія Теоретичні запитання.
- •Зразки практичних завдань.
- •Література.
Розділ II. Елементи аналітичної геометрії
Аналітична геометрія – це розділ математики, який вивчає геометричні об’єкти (поверхні, лінії, фігури) за допомогою методів алгебри, базуючись на методі координат. Метод координат дозволяє кожній точці поверхні або лінії поставити у відповідність сукупність чисел – координати. Кожна поверхня або лінія вважаються геометричним місцем точок, зв’язаних певними умовами і спільними властивостями. Згідно методу координат ці умови і властивості записуються у вигляді рівнянь або їх систем, які зв’язують між собою координати точок лінії або поверхні. Завдання поверхонь і ліній рівняннями відносно координат точок, що до них належать, дозволяє застосувати для їх дослідження методи алгебри, диференціального числення і апарат векторної алгебри.
126Equation Section 26§26. Поняття рівняння поверхні і лінії у просторі. Рівняння сферичної поверхні.
Розглянемо
довільне рівняння, що зв’язує між собою
три змінних
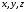 :
:
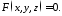 2262\* MERGEFORMAT (.)
2262\* MERGEFORMAT (.)
Припустимо,
що це рівняння має непорожню множину
розв’язків і
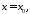
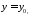
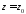 - один із них. Впорядкована трійка чисел
- один із них. Впорядкована трійка чисел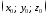 у прямокутній системі координат
у прямокутній системі координат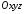 визначає точку
визначає точку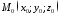 .
Сукупності всіх розв’язків рівняння
262 у цій системі координат відповідає
геометричне місце точок
.
Сукупності всіх розв’язків рівняння
262 у цій системі координат відповідає
геометричне місце точок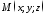 ,
яке називаєтьсяповерхнею
(Рис. 26.1).
,
яке називаєтьсяповерхнею
(Рис. 26.1).
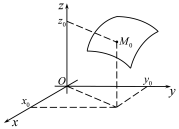
Рис. 26.1
Рівняння
262 називається рівнянням
поверхні
у заданій системі координат
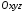 ,
якщо це рівняння задовольняють координати
кожної точки
,
якщо це рівняння задовольняють координати
кожної точки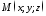 даної поверхні і не задовольняють
координати жодної точки, що лежить поза
поверхнею.
даної поверхні і не задовольняють
координати жодної точки, що лежить поза
поверхнею.
Стосовно
поверхонь аналітична геометрія має
розв’язувати наступні задачі: 1) якщо
поверхня задана як геометричне місце
точок, то необхідно скласти її рівняння
у даній системі координат; 2) по заданому
рівнянню 262 повинні у обраній системі
координат
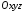 встановити, яку поверхню воно визначає
і дослідити її геометричні властивості.
встановити, яку поверхню воно визначає
і дослідити її геометричні властивості.
Як приклад розглянемо виведення рівняння сферичної поверхні або сфери.
Сферою (сферичною поверхнею) називається множина всіх точок простору, що знаходяться на однаковій відстані від заданої точки, яка називається центром. Відрізок, що з’єднує довільну точку сфери з центром називається радіусом і має бути заданим.
Нехай
у обраній системі координат
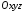 центром сфери є точка
центром сфери є точка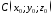 ,
а її радіус має довжину
,
а її радіус має довжину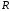 (Рис 26.2).
(Рис 26.2).
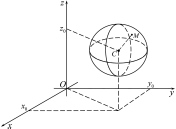
Рис. 26.2
Розглянемо
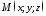 - довільну точку простору. Ця точка
належить сфері тоді і тільки тоді, коли
відстань від центра до неї дорівнює
радіусу:
- довільну точку простору. Ця точка
належить сфері тоді і тільки тоді, коли
відстань від центра до неї дорівнює
радіусу: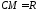 .
Але
.
Але

Отже, можна записати рівність
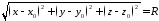 ,
,
яка після піднесення обох частин до квадрату набуває вигляду:
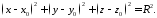 3263\* MERGEFORMAT (.)
3263\* MERGEFORMAT (.)
Якщо центр сфери збігається з початком координат, то рівняння 263 набуває вигляду:
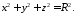
Можна
бачити, що рівняння 263 є рівнянням
другого порядку відносно
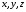 .
Тому кажуть, що сфера є алгебраїчною
поверхнею другого порядку.
.
Тому кажуть, що сфера є алгебраїчною
поверхнею другого порядку.
Лінія
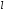 у тривимірному просторі може бути
утворена в результаті перетину двох
поверхонь
у тривимірному просторі може бути
утворена в результаті перетину двох
поверхонь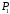 і
і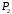 :
: (Рис. 26.3).
(Рис. 26.3).
Нехай ці поверхні визначаються рівняннями:
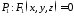 ,
,
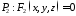 .
.
Тоді
координати будь-якої точки
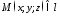 задовольнятимуть як перше так і друге
рівняння, тобто будуть розв’язками
системи
задовольнятимуть як перше так і друге
рівняння, тобто будуть розв’язками
системи
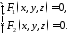 . 4264\* MERGEFORMAT (.)
. 4264\* MERGEFORMAT (.)
Систему рівнянь 264 називають загальним рівнянням лінії у просторі.
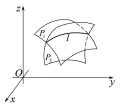
Рис.26 3
Також
лінією у просторі можна вважати
геометричне місце точок
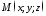 ,
кожна координата яких залежить від
деякої іншої змінної
,
кожна координата яких залежить від
деякої іншої змінної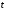 ,
яка називається параметром:
,
яка називається параметром:
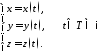 5265\* MERGEFORMAT (.)
5265\* MERGEFORMAT (.)
Рівняння
265 називають параметричним рівнянням
лінії у просторі. Якщо розглянути
 ‑ радіус-вектор довільної точки
‑ радіус-вектор довільної точки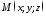 ,
яка належить лінії і ввести до розгляду
вектор
,
яка належить лінії і ввести до розгляду
вектор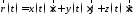 ,
то 265 можна записати у векторному
вигляді:
,
то 265 можна записати у векторному
вигляді:
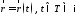 6266\* MERGEFORMAT (.)
6266\* MERGEFORMAT (.)
Рівняння 266 є векторне параметричне рівняння лінії.
Якщо
параметру
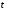 у 265 і 266 надати сенс часу, то лінія, що
ними визначається, це траєкторія, по
якій рухається матеріальна точка
у 265 і 266 надати сенс часу, то лінія, що
ними визначається, це траєкторія, по
якій рухається матеріальна точка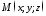 .
.
727Equation Section (Next)§27. Загальне рівняння площини і його дослідження.
Найбільш
простою за властивостями поверхнею є
площина. Площина як геометричне місце
точок простору може бути визначена за
допомогою ненульового вектора
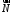 ,
до якого вона перпендикулярна, і точки
,
до якого вона перпендикулярна, і точки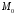 ,
через яку вона проходить. Оберемо у
просторі систему координат
,
через яку вона проходить. Оберемо у
просторі систему координат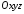 і розглянемо площину, що проходить через
точку
і розглянемо площину, що проходить через
точку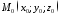 перпендикулярно до вектора
перпендикулярно до вектора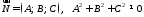 (Рис.27.1).
(Рис.27.1).
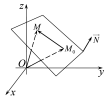
Рис. 27.1
Візьмемо
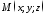 ‑ довільну точку площини і розглянемо
вектори
‑ довільну точку площини і розглянемо
вектори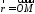 ,
,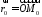 .
Вектор
.
Вектор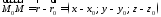 для кожної точки, що належить площині,
перпендикулярний до вектора
для кожної точки, що належить площині,
перпендикулярний до вектора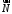 .
Згідно умові перпендикулярності:
.
Згідно умові перпендикулярності:
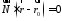 або
або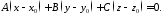 8278\* MERGEFORMAT (.)
8278\* MERGEFORMAT (.)
Рівняння
278 є рівнянням площини, що проходить
через задану точку
 перпендикулярно до заданого вектора
перпендикулярно до заданого вектора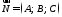 .
.
Останню рівність можна записати наступним чином:
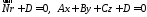 , 9279\* MERGEFORMAT (.)
, 9279\* MERGEFORMAT (.)
де
 .
.
Можна
довести, що будь-яке рівняння 279 першого
степеня відносно
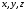 визначає у системі
визначає у системі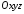 площину, перпендикулярну до вектора
площину, перпендикулярну до вектора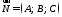 .
Тому рівняння 279 називаєтьсязагальним
рівнянням площини.
Вектор
.
Тому рівняння 279 називаєтьсязагальним
рівнянням площини.
Вектор
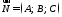 називаєтьсянормальним
вектором
площини.
називаєтьсянормальним
вектором
площини.
Оскільки
рівняння 279 містить лише перші степені
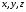 ,
то площина є алгебраїчною поверхнею
першого степеня.
,
то площина є алгебраїчною поверхнею
першого степеня.
Здійснимо дослідження загального рівняння площини 279. Це дослідження буде полягати у з’ясуванні розташування площини відносно координатних осей при деяких частинних випадках рівняння 279.
Нехай у рівнянні 279
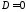 :
:
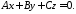 102710\* MERGEFORMAT (.)
102710\* MERGEFORMAT (.)
Можна
бачити, що
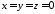 є розв’язком цього рівняння, значить
точка
є розв’язком цього рівняння, значить
точка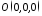 належить площині. Тобто у разі відсутності
у загальному рівнянні вільного члена
площина проходить через початок
координат.
належить площині. Тобто у разі відсутності
у загальному рівнянні вільного члена
площина проходить через початок
координат.
При
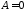 рівняння 279 набуває вигляду
рівняння 279 набуває вигляду
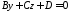 112711\* MERGEFORMAT (.)
112711\* MERGEFORMAT (.)
і
визначає площину, що перпендикулярна
вектору
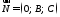 ,
який є перпендикулярним до осі
,
який є перпендикулярним до осі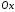 .
Отже площина, що визначається рівнянням
2711 паралельна осі
.
Отже площина, що визначається рівнянням
2711 паралельна осі .
Аналогічно встановлюється, що площини,
задані рівняннями
.
Аналогічно встановлюється, що площини,
задані рівняннями
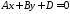 ‑ паралельні осі
‑ паралельні осі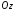 ; 122712\* MERGEFORMAT (.)
; 122712\* MERGEFORMAT (.)
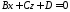 ‑ паралельні осі
‑ паралельні осі
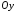 .
.
Якщо
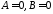 ,
а
,
а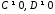 ,
то рівняння 279 набуває вигляду:
,
то рівняння 279 набуває вигляду:
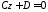 або
або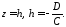 132713\* MERGEFORMAT (.)
132713\* MERGEFORMAT (.)
Нормальний
вектор цієї площини
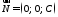 перпендикулярний до осей
перпендикулярний до осей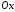 і
і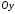 ,
тобто перпендикулярний до площини
,
тобто перпендикулярний до площини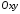 .
Тому площина, що визначається рівнянням
2713, є паралельною до координатної
площини
.
Тому площина, що визначається рівнянням
2713, є паралельною до координатної
площини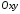 .
Коли при цьому і
.
Коли при цьому і ,
то 2713 має вигляд
,
то 2713 має вигляд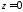 і визначає саму площину
і визначає саму площину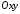 .
.
Відповідно:
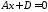 ‑ рівняння площини, паралельної до
‑ рівняння площини, паралельної до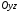 ,
,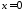 ‑ рівняння самої площини
‑ рівняння самої площини .
.
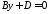 ‑ рівняння площини, паралельної до
‑ рівняння площини, паралельної до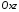 ,
, ‑ рівняння самої площини
‑ рівняння самої площини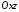 .
.
1428Equation Section (Next)§28. Рівняння площини у відрізках на координатних осях. Рівняння площини, що проходить через три задані точки. Обчислення відстані від точки до площини
Розглянемо
площину, яка у системі координат
 задана загальним рівнянням 279, у якому
задана загальним рівнянням 279, у якому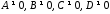 .
Тоді в результаті ділення обох частин
279 на коефіцієнт
.
Тоді в результаті ділення обох частин
279 на коефіцієнт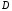 це рівняння можна переписати у вигляді
це рівняння можна переписати у вигляді
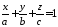 , 152815\* MERGEFORMAT (.)
, 152815\* MERGEFORMAT (.)
де
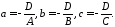
Можна
бачити, що точки
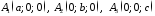 задовольняють рівняння 2815, тобто
належать площині і є точками перетину
цієї площини з осями координат (Рис.28.1).
задовольняють рівняння 2815, тобто
належать площині і є точками перетину
цієї площини з осями координат (Рис.28.1).
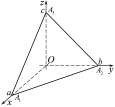
Рис. 28.1
Таким
чином, якщо відомі точки перетину площини
з осями координат, то її рівняння може
бути записаним у вигляді 2815. Оскільки
числа
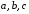 з точністю до знаку співпадають з
довжинами відрізків, які площини відтинає
на координатних осях:
з точністю до знаку співпадають з
довжинами відрізків, які площини відтинає
на координатних осях: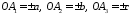 ,
то рівняння 2815 ще називаютьсярівнянням
площини у відрізках на
координатних осях.
,
то рівняння 2815 ще називаютьсярівнянням
площини у відрізках на
координатних осях.
Розглянемо
тепер три довільні точки
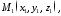
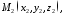
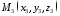 ,
які не знаходяться на одній прямій. Як
відомо, тоді існує єдина площина, що
проходить через ці точки. Знайдемо її
рівняння.
,
які не знаходяться на одній прямій. Як
відомо, тоді існує єдина площина, що
проходить через ці точки. Знайдемо її
рівняння.
Для
цього візьмемо на площині довільну
точку
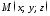 і розглянемо вектори
і розглянемо вектори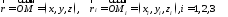 (Рис.28.2):
(Рис.28.2):
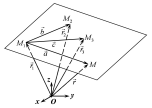
Рис. 28.2
Тепер,
якщо взяти вектори
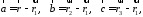 то вони знаходяться у одній площині і
є компланарними. Тоді їх мішаний добуток
має дорівнювати нулю:
то вони знаходяться у одній площині і
є компланарними. Тоді їх мішаний добуток
має дорівнювати нулю:
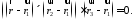 162816\* MERGEFORMAT (.)
162816\* MERGEFORMAT (.)
Рівняння
2816 містить
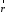 - радіус-вектор довільної площини і є
векторною формою рівняння площини, що
проходить через три задані точки.
Координатну форму рівняння 2816 отримаємо,
коли скористаємося формулою для мішаного
добутку:
- радіус-вектор довільної площини і є
векторною формою рівняння площини, що
проходить через три задані точки.
Координатну форму рівняння 2816 отримаємо,
коли скористаємося формулою для мішаного
добутку:
 172817\* MERGEFORMAT (.)
172817\* MERGEFORMAT (.)
Після
обчислення визначника 2817 перетвориться
у лінійне рівняння відносно
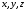 ,
яке і є загальним рівнянням площини, що
проходить через три задані точки.
,
яке і є загальним рівнянням площини, що
проходить через три задані точки.
Розв'яжемо
методами аналітичної геометрії задачу,
яка має важливе значення для теорії
навігації і картографії. А саме, визначення
відстані від заданої точки до заданої
площини. Нехай у системі координат
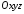 задано
точку
задано
точку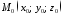 і площину, яка визначається рівнянням
279.
Проведемо з точки
і площину, яка визначається рівнянням
279.
Проведемо з точки
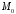 на площину перпендикуляр, який перетне
її у точці
на площину перпендикуляр, який перетне
її у точці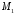 (Рис.28.3).
Тоді довжина цього перпендикуляра
(Рис.28.3).
Тоді довжина цього перпендикуляра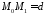 і є відстань від точки до площини.
Розглянемо вектори
і є відстань від точки до площини.
Розглянемо вектори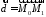 і
і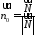 -
одиничний вектор, нормальний до площини.
-
одиничний вектор, нормальний до площини.
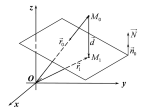
Рис. 28.3
Оскільки
ці вектори колінеарні і
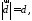 а
а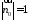 ,
то
,
то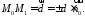 Знак залежить від розміщення точки
Знак залежить від розміщення точки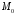 відносно площини. Позначимо
відносно площини. Позначимо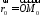 ,
,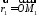 .
Тоді з векторного трикутника
.
Тоді з векторного трикутника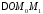 (Рис.28.3) маємо:
(Рис.28.3) маємо:
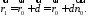 182818\* MERGEFORMAT (.)
182818\* MERGEFORMAT (.)
Але
точка
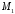 належить площині і її радіус-вектор
належить площині і її радіус-вектор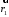 має задовольняти векторне рівняння
279.
В результаті підстановки 2818
у
279 знаходимо
має задовольняти векторне рівняння
279.
В результаті підстановки 2818
у
279 знаходимо
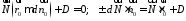 .
.
Оскільки
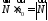 ,
то
,
то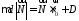 .
.
Абсолютні величини лівої та правої частин останньої рівності мають співпадати.
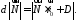
Остаточно знаходимо формулу для відстані:
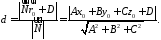 192819\* MERGEFORMAT (.)
192819\* MERGEFORMAT (.)
2029Equation Section (Next)§29. Кут між двома площинами. Умови паралельності і перпендикулярності площин
Нехай
є дві площини
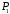 і
і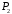 ,
які в системі координат
,
які в системі координат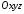 задаються рівняннями
задаються рівняннями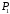 :
: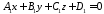 ;
;
 :
: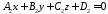 .
.
Якщо
ці площини паралельні, то їх нормальні
вектори
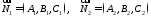 колінеарні. Тому умовою паралельності
двох площин є умова колінеарності цих
векторів:
колінеарні. Тому умовою паралельності
двох площин є умова колінеарності цих
векторів:
 212921\* MERGEFORMAT (.)
212921\* MERGEFORMAT (.)
Коли
площини не паралельні, то вони утворюють
двогранний кут, що вимірюється гострим
лінійним кутом
 або тупим
або тупим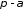 (Рис.29.1). Один з лінійних кутів гострий
або тупий співпадає з кутом
(Рис.29.1). Один з лінійних кутів гострий
або тупий співпадає з кутом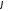 між нормальними векторами площин.
між нормальними векторами площин.
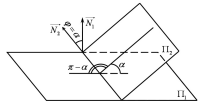
Рис.29.1
За формулою для визначення кута між векторами маємо:
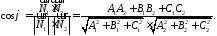 222922\* MERGEFORMAT (.)
222922\* MERGEFORMAT (.)
Якщо
результат, отриманий за формулою 2922,
додатній, то
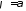 ,
а якщо від'ємний, то
,
а якщо від'ємний, то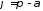 .
.
Умовою перпендикулярності двох площин є умова перпендикулярності їх нормальних векторів:
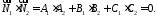 232923\* MERGEFORMAT (.)
232923\* MERGEFORMAT (.)
2430Equation Section (Next)§30. Розв'язання задач на складання рівнянь площини та взаємне розміщення площин у просторі
Задача
30.1.
Скласти
рівняння площини, що проходить через
точку
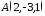 перпендикулярно до вектора
перпендикулярно до вектора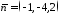 .
.
Розв’язання.
Рівняння площини, що проходить через точку перпендикулярно до заданого вектора має вигляд 278. У нашому випадку рівняння набуває вигляду:
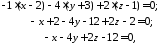
або
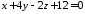 -загальне
рівняння площини.
-загальне
рівняння площини.
Задача
30.2.
Скласти рівняння площини, яка проходить
через точку
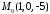 паралельно двом векторам
паралельно двом векторам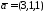 та
та .
.
Розв’язання.
Оскільки вектори не колінеарні, зобразимо їх з початком у одній точці і розглянемо площину, яка їм паралельна (Рис.30.1).
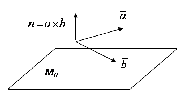
Рис.30.1
Відомо,
що векторний добуток двох векторів
перпендикулярний до обох
векторів-співмножників, тому за нормальний
вектор площини можна взяти векторний
добуток
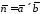 ,
а саме
,
а саме
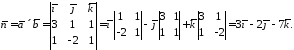
Тепер рівняння площини набуде вигляду
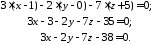
Задача
30.3.
Дано
точки перетину площини з координатними
осями:
 ,
,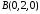 ,
,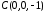 .
Скласти її рівняння.
.
Скласти її рівняння.
Розв’язання.
З
умови задачі відомо, що задана площина
відтинає на координатних осях
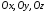 відрізки
відрізки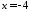 ,
,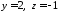 відповідно. Отже, згідно 2815, шукане
рівняння площини набуде вигляду:
відповідно. Отже, згідно 2815, шукане
рівняння площини набуде вигляду:
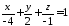 ,
або
,
або
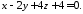
Задача
30.4.
Скласти рівняння площини, що проходить
через три точки
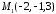 ,
,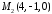 та
та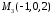 .
Знайти довжини відрізків, які відтинає
утворена площина на координатних осях.
.
Знайти довжини відрізків, які відтинає
утворена площина на координатних осях.
Розв’язання.
Для складання рівняння площини використаємо формулу 2817. Отримаємо:
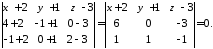
Отриманий визначник розкладемо за елементами 1 рядка:
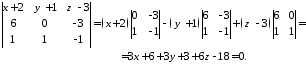
Після приведення подібних членів запишемо загальне рівняння площини:
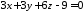 або
або
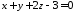 .
.
Знайдемо відрізки, які відтинає утворена площина на координатних осях. Для цього приведемо отримане рівняння до вигляду рівняння у відрізках 2815:
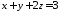 ;
;
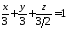 .
.
Отже,
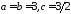 -
довжини відрізків, що відтинаються
площиною на координатних осях
-
довжини відрізків, що відтинаються
площиною на координатних осях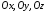 відповідно.
відповідно.
Задача
30.5.
Скласти
рівняння площини, що проходить через
дві точки
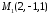 ,
,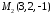 перпендикулярно до площини
перпендикулярно до площини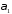 :
: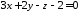 .
.
Розв’язання.
Зобразимо
задану площину
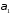 та
перпендикулярну до неї площину
та
перпендикулярну до неї площину
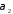 ,
яка проходить через задані точки
(Рис.30.2).
,
яка проходить через задані точки
(Рис.30.2).
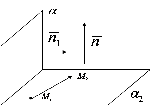
Рис.30.2
З
рисунку зрозуміло, що нормальний вектор
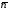 шуканої
площини
шуканої
площини
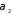 перпендикулярний
як вектору
перпендикулярний
як вектору
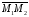 ,
так і нормальному вектору
,
так і нормальному вектору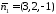 заданої площини
заданої площини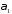 ,
тому його можна обчислити як векторний
добуток цих векторів.
,
тому його можна обчислити як векторний
добуток цих векторів.
Знайдемо
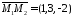 .
Далі
.
Далі
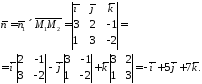
Шукана
площина проходить через точку
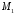 і
і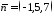 - її нормальний вектор. Запишемо рівняння
цієї площини:
- її нормальний вектор. Запишемо рівняння
цієї площини:
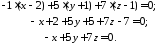
Задача
30.6.
Скласти
рівняння площини, що проходить через
точки
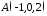 та
та
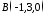 паралельно осі
паралельно осі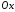 .
.
Розв’язання.
Оскільки
шукана площина проходить паралельно
осі
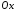 ,
то її нормальним вектором може бути
векторний добуток неколінеарних векторів
,
то її нормальним вектором може бути
векторний добуток неколінеарних векторів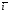 та
та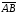 :
:
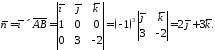
Тепер
згідно 278 запишемо рівняння площини,
що проходить через точку
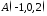 перпендикулярно
вектору
перпендикулярно
вектору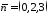 :
:
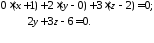
Задача
30.7.
Скласти
рівняння площини, що проходить через
точку
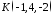 паралельно площині
паралельно площині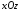 .
.
Розв’язання.
1
спосіб.
Оскільки за умовою задачі шукана площина
паралельна до площини
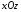 ,
то вона перпендикулярна до осі
,
то вона перпендикулярна до осі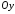 .
А значить, вектор з координатами
.
А значить, вектор з координатами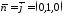 буде нормальним для шуканої площини.
Тоді рівняння цієї площини має вигляд:
буде нормальним для шуканої площини.
Тоді рівняння цієї площини має вигляд:
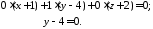
2
спосіб.
Рівняння площини, паралельної до площини
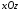 має вигляд
має вигляд
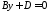 . 253025\* MERGEFORMAT (.)
. 253025\* MERGEFORMAT (.)
Точка
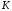 належить площині, отже, її координати
задовольняють 3025:
належить площині, отже, її координати
задовольняють 3025:
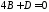 ,
звідки
,
звідки
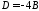 .
.
Підставляючи це значення в неповне рівняння площини 3025, отримаємо
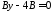 ,
,
а
після скорочення на
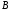 остаточно матимемо шукане рівняння:
остаточно матимемо шукане рівняння:
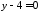 .
.
Задача
30.8.
Скласти
рівняння площини, що проходить через
вісь
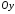 та точку
та точку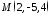 .
.
Розв’язання.
Так
як шукана площина проходить через вісь
 ,
то її рівняння має вигляд
,
то її рівняння має вигляд
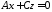 .
.
Підставимо
в це рівняння координати точки
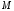 ,
що належить площині:
,
що належить площині:
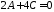 ,
звідки
,
звідки
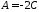 .
.
Після
підстановки отриманого значення
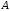 в неповне рівняння, отримуємо
в неповне рівняння, отримуємо
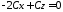 або
або
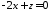 .
.
Задача
30.9.
При
яких значеннях
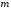 та
та
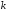 площини
площини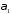 та
та
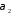 паралельні, якщо
паралельні, якщо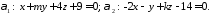
Розв’язання.
Дані
в умові задачі площини мають нормальні
вектори
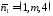 ,
, .
Використаємо умову паралельності двох
площин 2921:
.
Використаємо умову паралельності двох
площин 2921:
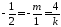 ,
що справедливо при
,
що справедливо при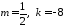 .
.
Задача
30.10.
Знайти
косинус кута між площинами
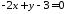 та
та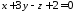 .
.
Розв’язання.
Площини
мають наступні нормальні вектори:
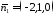 ,
,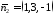 .
Відповідно до формули 2922 маємо:
.
Відповідно до формули 2922 маємо:
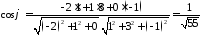 .
.
Задача
30.11.
Знайти відстань від точки
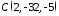 до площини
до площини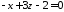 .
.
Розв’язання.
Для обчислення відстані від точки до площини скористаємось формулою 2819:
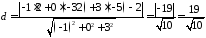 .
.
Задача
30.12.
Записати
рівняння площини, що проходить через
точку
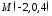 і відтинає на осях
і відтинає на осях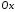 та
та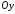 удвічі більші відрізки, ніж на осі
удвічі більші відрізки, ніж на осі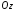 .
.
Розв’язання.
Нехай
на осі
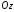 площина відтинає відрізок довжини
площина відтинає відрізок довжини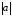 ,
тоді на двох інших осях відрізки
,
тоді на двох інших осях відрізки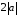 .Використаємо
рівняння площини у відрізках:
.Використаємо
рівняння площини у відрізках:
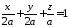 .
.
Точка
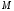 належить
площині, отже, її координати задовольняють
рівняння 2815:
належить
площині, отже, її координати задовольняють
рівняння 2815:
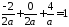 .
.
З
останього рівняння знаходимо, що
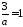 ,
отже,
,
отже,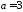 .
.
Таким чином, рівняння площини має вигляд:
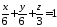 .
.
