
- •Розділ II. Елементи аналітичної геометрії
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •1) Підставимо в канонічне рівняння еліпса 4078 замість такоординати точкиА, а також дане значення . Одержимо рівняння:.
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •§ 48. Розв’язування задач на складання рівнянь поверхонь та їх дослідження
- •Задачі для самостійної роботи
- •Питання для повторення
- •Відповіді
- •Додаток
- •Програма модульного контролю з теми
- •Лінійна і векторна алгебра
- •Теоретичні запитання.
- •Зразки практичних завданнь.
- •Програма модульного контролю з теми аналітична геометрія Теоретичні запитання.
- •Зразки практичних завдань.
- •Література.
Задачі для самостійної роботи
Записати рівняння прямої з кутовим коефіцієнтом, якщо їй належать точки
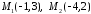
Задано вершини трикутника:
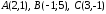 .
Знайти рівняння висоти, що проведена
із вершиниС.
.
Знайти рівняння висоти, що проведена
із вершиниС.
Довести, що прямі
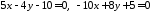 паралельні і обчислити відстань між
ними.
паралельні і обчислити відстань між
ними.Дано точки:
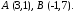 Скласти рівняння прямої, яка проходить
через середину відрізкаAB
перпендикулярно цьому відрізку.
Скласти рівняння прямої, яка проходить
через середину відрізкаAB
перпендикулярно цьому відрізку.Обчислити відстань від точки
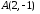 до прямої
до прямої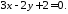
Визначити кут між двома прямими
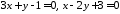 .
.Скласти рівняння медіани АМ трикутника з вершинами
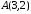 ,
,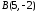 ,
,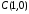 .
.Дано дві точки
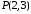 та
та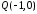 .
Скласти рівняння прямої, що проходить
через точкуQ
перпендикулярно до відрізку PQ.
.
Скласти рівняння прямої, що проходить
через точкуQ
перпендикулярно до відрізку PQ.Через точки
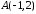 та
та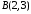 проведено пряму. Визначити точки
перетину цієї прямої з осями координат.
проведено пряму. Визначити точки
перетину цієї прямої з осями координат.Знайти рівняння прямої, яка проходить через точку перетину прямих
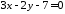 і
і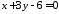 та точку
та точку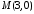 .
.Знайти рівняння прямої, яка проходить через точку
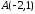 паралельно прямій
паралельно прямій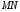 ,
якщо
,
якщо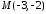 ,
,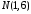 .
.Знайти точку, симетричну точці
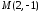 відносно прямої
відносно прямої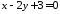 .
.Знайти точку
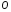 перетину діагоналей чотирикутника
перетину діагоналей чотирикутника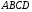 ,
якщо
,
якщо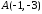 ,
,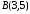 ,
,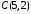 ,
,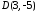 .
.Скласти рівняння висоти, яка проведена через вершину
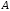 трикутника
трикутника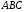 ,
якщо відомі рівняння його сторін:
,
якщо відомі рівняння його сторін: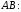
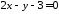 ,
,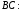
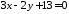 ,
,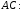
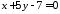 .
.Записати рівняння прямої, яка проходить через точку
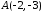 та утворює з віссю
та утворює з віссю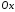 кути: а)
кути: а)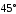 ,
б)
,
б)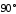 ,
в)
,
в)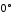 .
.Задано рівняння висот трикутника
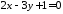 ,
,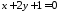 та координати його вершини
та координати його вершини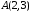 .
Знайти рівняння сторін
.
Знайти рівняння сторін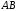 та
та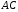 трикутника.
трикутника.Подані рівняння двох сторін паралелограма
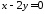 ,
,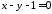 та точка перетину його діагоналей
та точка перетину його діагоналей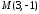 .
Знайти рівняння двох інших сторін.
.
Знайти рівняння двох інших сторін.
Питання для повторення
Рівняння кола. Загальне рівняння прямої на площині.
Види рівнянь прямої на координатній площині.
Відстань від точки до прямої на площині. Кут між прямими.
7540Equation Section (Next)§40. Визначення еліпса і виведення його канонічного рівняння. Дослідження форми еліпса за його рівнянням
Еліпсом
називається множина усіх точок площини,
для яких сума відстаней від кожної до
двох заданих точок, які називаються
фокусами,
є сталою величиною. Нехай
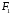 і
і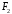 - фокуси еліпса. Для виведення рівняння
еліпса система координат обирається,
так щоб фокуси знаходились на осі
- фокуси еліпса. Для виведення рівняння
еліпса система координат обирається,
так щоб фокуси знаходились на осі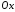 ,
а початкова точка співпадала з серединою
відрізка
,
а початкова точка співпадала з серединою
відрізка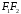 .
Осі координат спрямовуються так, щоб
система
.
Осі координат спрямовуються так, щоб
система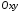 була правою. (Рис. 40.1)
була правою. (Рис. 40.1)
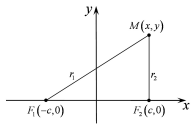
Рис. 40.1
Нехай
в обраній системі координат фокуси
мають координати
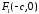 ,
,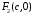 .
Візьмемо довільну точку еліпса
.
Візьмемо довільну точку еліпса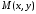 . Відрізки, що з’єднують точку еліпса
з фокусами, називаютьсяфокальними
радіусами
точки. Позначимо їх
. Відрізки, що з’єднують точку еліпса
з фокусами, називаютьсяфокальними
радіусами
точки. Позначимо їх
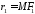 ,
,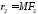 .
Згідно визначення для будь-якої точки
на еліпсі сума фокальних радіусів стала
величина, яку позначимо
.
Згідно визначення для будь-якої точки
на еліпсі сума фокальних радіусів стала
величина, яку позначимо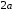 :
:
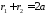 . 764076\* MERGEFORMAT (.)
. 764076\* MERGEFORMAT (.)
Причому
за властивостями сторін трикутника
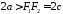 ,
отже,
,
отже,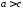 .
.
Фокальні радіуси дорівнюють
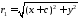 ,
,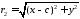 .774077\* MERGEFORMAT (.)
.774077\* MERGEFORMAT (.)
Підставимо 4077 у 4076
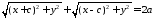
і отриману рівність перетворимо до вигляду:
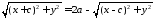 .
.
Далі обидві частини останньої рівності підносимо до квадрату і спрощуємо:
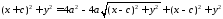 ,
,
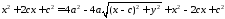 ,
,
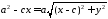 .
.
Знову підносимо обидві частини рівності до квадрату:
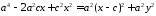 ,
,
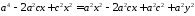 ,
,
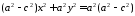 .
.
Оскільки
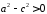 ,
то введемо позначення
,
то введемо позначення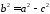 і знайдемо з останнього
і знайдемо з останнього
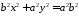 .
.
Після
ділення на
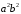 обох частин остаточно знаходимо
обох частин остаточно знаходимо
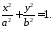 784078\* MERGEFORMAT (.)
784078\* MERGEFORMAT (.)
Рівняння 4078 називається канонічним рівнянням еліпса.
У
рівняння 4078 координати
 і
і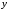 входять у другій степені, тому кажуть,
що еліпс – крива другого порядку.
входять у другій степені, тому кажуть,
що еліпс – крива другого порядку.
Виведене рівняння 4078 дозволяє встановити наступні властивості еліпса.
Обмеженість еліпса. З рівняння 4078 випливає
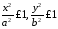 або
або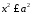 ,
,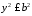 чи
чи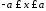 ,
,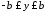 .
Геометрично ці нерівності означають,
що еліпс – це обмежена лінія, яка
знаходиться у прямокутнику, утвореному
прямими
.
Геометрично ці нерівності означають,
що еліпс – це обмежена лінія, яка
знаходиться у прямокутнику, утвореному
прямими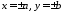 .
.Симетричність і точки перетину з координатними осями. Оскільки координати
 і
і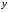 входять у 4078 тільки у квадраті, то з
того, що точка
входять у 4078 тільки у квадраті, то з
того, що точка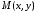 належить еліпсу, випливає, що і точки
належить еліпсу, випливає, що і точки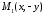 ,
,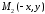 ,
,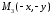 належать цьому еліпсу. Це означає, що
осі
належать цьому еліпсу. Це означає, що
осі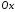 і
і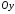 є осями симетрії еліпса, а точка
є осями симетрії еліпса, а точка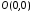 -
його центром. Оскільки еліпс має центр
симетрії, то він є центральною кривою.
-
його центром. Оскільки еліпс має центр
симетрії, то він є центральною кривою.
При
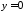 з 4078 маємо
з 4078 маємо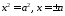 .
Отже, точки
.
Отже, точки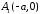 ,
,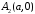 є точками перетину еліпса з віссю
є точками перетину еліпса з віссю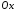 .
Якщо
.
Якщо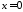 ,
то
,
то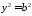 ,
,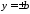 і точки
і точки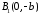 і
і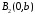 є точками перетину еліпса з віссю
є точками перетину еліпса з віссю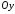 (Рис. 40.2). Точки перетину еліпса з осями
координат називаються йоговершинами.
Відрізок
(Рис. 40.2). Точки перетину еліпса з осями
координат називаються йоговершинами.
Відрізок
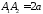 називаєтьсявеликою
віссю
еліпса, а відрізки
називаєтьсявеликою
віссю
еліпса, а відрізки
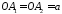 великими
півосями.
Відрізок
великими
півосями.
Відрізок
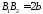 називаєтьсямалою
віссю
еліпса, а відрізки
називаєтьсямалою
віссю
еліпса, а відрізки
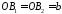 йогомалими
півосями.
йогомалими
півосями.
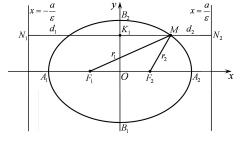
Рис. 40.2
Ексцентриситет еліпса. Обчислення фокальних радіусів точки на еліпсі.
Ексцентриситетом еліпса називається відношення відстані між фокусами до довжини великої осі:
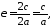 794079\* MERGEFORMAT (.)
794079\* MERGEFORMAT (.)
або,
оскільки
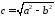 ,
,
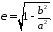 804080\* MERGEFORMAT (.)
804080\* MERGEFORMAT (.)
Можна
бачити, що ексцентриситет може приймати
значення
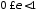 .
З 4080 випливає,що чим більше ексцентриситет,
тим менше мала вісь за велику і тим
більше витягнутий еліпс вздовж великої
осі. У граничному випадку
.
З 4080 випливає,що чим більше ексцентриситет,
тим менше мала вісь за велику і тим
більше витягнутий еліпс вздовж великої
осі. У граничному випадку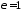 маємо
маємо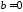 і еліпс перетворюється у відрізок
і еліпс перетворюється у відрізок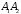 .
При
.
При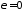
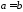 ,
,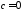 ,
тобто фокуси еліпса співпадають, а сам
він перетворюється у коло радіуса
,
тобто фокуси еліпса співпадають, а сам
він перетворюється у коло радіуса .
Це коло, як випливає з 4078, визначається
рівнянням
.
Це коло, як випливає з 4078, визначається
рівнянням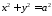 .
.
За допомогою ексцентриситету можна знайти прості вирази для фокальних радіусів точки на еліпсі. Дійсно, з 4078 знаходимо
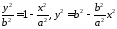
і підставляємо у формули для фокальних радіусів (11.2):
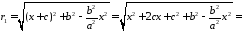
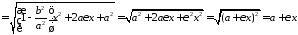 .
.
Враховано,
що завжди
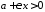 .
.
Після аналогічних перетворень для другого фокального радіуса знаходимо остаточно
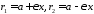 . 814081\* MERGEFORMAT (.)
. 814081\* MERGEFORMAT (.)
Директриси еліпса і їх властивості.
Прямі (Рис. 40.2)
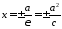 824082\* MERGEFORMAT (.)
824082\* MERGEFORMAT (.)
називаються
директрисами
еліпса. Головною властивістю директис
є наступна: відношення фокального
радіуса точки еліпса до відстані від
неї до відповідної директриси дорівнює
ексцентриситету еліпса. Тобто, якщо
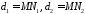 (Рис. 40.2), то
(Рис. 40.2), то
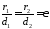 . 834083\* MERGEFORMAT (.)
. 834083\* MERGEFORMAT (.)
Дійсно,
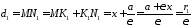 ,
,
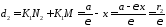 .
Звідси випливають рівності 4083.
.
Звідси випливають рівності 4083.
8441Equation Section (Next)§ 41. Визначення гіперболи і виведення її канонічного рівняння. Дослідження форми гіперболи за її рівнянням
Гіперболою називається множина точок площини, модуль різниці відстаней від кожної з яких до двох заданих точок, які називаються фокусами, є величина стала.
Нехай
точки
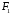 і
і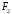 - це фокуси гіперболи. Для виведення її
рівняння система координат обирається
так само, як і у випадку еліпса (Рис.
40.1). Відрізки, що з’єднують довільну
точку гіперболи
- це фокуси гіперболи. Для виведення її
рівняння система координат обирається
так само, як і у випадку еліпса (Рис.
40.1). Відрізки, що з’єднують довільну
точку гіперболи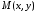 з фокусами, називаються їїфокальними
радіусами
(Рис. 40.1) і знаходяться за формулами 4077.
Згідно визначення гіперболи модуль
різниці фокальних радіусів для точок
гіперболи – це стала величина, яку
позначимо
з фокусами, називаються їїфокальними
радіусами
(Рис. 40.1) і знаходяться за формулами 4077.
Згідно визначення гіперболи модуль
різниці фокальних радіусів для точок
гіперболи – це стала величина, яку
позначимо
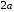 .
З властивостей сторін трикутника
.
З властивостей сторін трикутника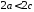 ,
,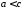 .
Тоді має виконуватись рівність:
.
Тоді має виконуватись рівність:
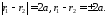 854185\* MERGEFORMAT (.)
854185\* MERGEFORMAT (.)
Після підстановки у 4185 фокальних радіусів з 4077 отримаємо:
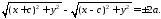 864186\* MERGEFORMAT (.)
864186\* MERGEFORMAT (.)
Внаслідок перетворень останнього рівняння, аналогічно проведеним у випадку еліпса, приходимо до наступного:
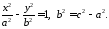 874187\* MERGEFORMAT (.)
874187\* MERGEFORMAT (.)
Рівняння 4187 називається канонічним рівнянням гіперболи. Як і еліпс, гіпербола є кривою другого порядку.
Встановимо основні властивості гіперболи.
З 4187 можна бачити що
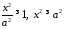 , тобто
, тобто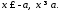 Це означає, що гіпербола - необмежена
лінія, яка складається з двох частин,
що розміщуються у частинах координатної
площини
Це означає, що гіпербола - необмежена
лінія, яка складається з двох частин,
що розміщуються у частинах координатної
площини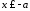 та
та
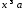 .Ці
частини гіперболи називаються її
гілками.
.Ці
частини гіперболи називаються її
гілками.
Як і еліпс, гіпербола симетрична відносно осей
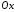 і
і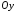 і точки
і точки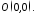 Таким чином, гіпербола - це теж центральна
крива.
Таким чином, гіпербола - це теж центральна
крива.
Точки
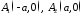 є точками перетину гіперболи з віссю
є точками перетину гіперболи з віссю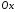 і називаються їївершинами.
З віссю
і називаються їївершинами.
З віссю
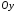 гіпербола не перетинається.
гіпербола не перетинається.
Відрізок
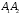 називаєтьсядійсною
віссю
гіперболи, а відрізок
називаєтьсядійсною
віссю
гіперболи, а відрізок
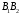 називається їїуявною
віссю.
називається їїуявною
віссю.
Асимптоти гіперболи.
Здійснимо над рівнянням 4187 наступне перетворення:
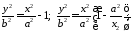
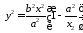 884188\* MERGEFORMAT (.)
884188\* MERGEFORMAT (.)
Ця рівність означає, що для будь-якої точки гіперболи виконується нерівність
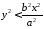 ,
або
,
або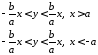 894189\* MERGEFORMAT (.)
894189\* MERGEFORMAT (.)
Нерівності 4189 означають, що точки гіпербли знаходяться у частині координатної площини, обмеженої прямими
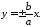 904190\* MERGEFORMAT (.)
904190\* MERGEFORMAT (.)
Розглянемо
величину
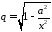 .
Тоді з 4188 можно записати:
.
Тоді з 4188 можно записати:
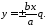
Величина
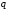 лежить у межах
лежить у межах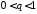 і прямує до
і прямує до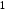 ,
коли
,
коли
 прямує до нескінченності. Це означає,
що при прямуванні
прямує до нескінченності. Це означає,
що при прямуванні до нескінченності точки гіперболи і
точки прямих 4190 необмежено зближуються.
Прямі 4190 називаютьсяасимптотами
гіперболи. Вони є діагоналями прямокутника,
що утворюють прямі
до нескінченності точки гіперболи і
точки прямих 4190 необмежено зближуються.
Прямі 4190 називаютьсяасимптотами
гіперболи. Вони є діагоналями прямокутника,
що утворюють прямі
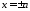 і
і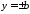 .
Він називається основним прямокутником
гіперболи.
.
Він називається основним прямокутником
гіперболи.
Встановлені властивості дають можливість зобразити гіперболу (Рис. 41.1).
Ексцентриситет гіперболи і формули для фокальних радіусів.
Ексцентриситетом гіперболи називається відношення відстані між фокусами до довжини дійсної осі:
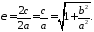 914191\* MERGEFORMAT (.)
914191\* MERGEFORMAT (.)
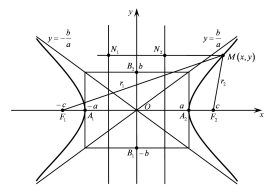
Рис. 41.1
З 4191 знаходимо
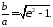
З останньої формули можна бачити, що ексцентриситет гіперболи характеризує форму її основного прямокутника, а значить і форму гіперболи.
Окрім того, поняття ексецентриситета дає можливість знайти прості формули для фокальних радіусів точки на гіперболі:
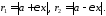 924192\* MERGEFORMAT (.)
924192\* MERGEFORMAT (.)
Виведення цих формул здійснено аналогічно виведенню формул 4081 для еліпса.
Директриси гіперболи.
Директрисами гіперболи називаються прямі, що визначаються рівняннями
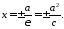 934193\* MERGEFORMAT (.)
934193\* MERGEFORMAT (.)
Директриси
гіперболи мають властивості, аналогічні
до директрис еліпса. Якщо
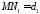 і
і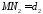 - відстані від точки гіперболи до
директрис (Рис. 41.1), то завжди виконується
рівність
- відстані від точки гіперболи до
директрис (Рис. 41.1), то завжди виконується
рівність
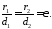
Таким чином, відношення фокального радіуса точки гіперболи до відстані від неї до відповідної директриси дорівнює ексцентриситету гіперболи.
9442Equation Section (Next)§ 42. Визначення параболи і виведення її канонічного рівняння. Дослідження форми і властивостей параболи
Параболою називається множина точок площини, кожна з яких знаходиться на однаковій відстані від заданої точки, яка називається фокусом, і від даної прямої, яка не проходить через фокус і називається директрисою.
Відстань
від фокуса до директриси називається
параметром
параболи
і далі позначається
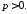
Для
виведення рівняння параболи вводимо
систему координат
 таким чином. Вісь
таким чином. Вісь проходить через фокус перпендикулярно
до директриси і додатній напрямок
задається від директриси до фокуса.
Початок координат помістимо посередині
між фокусом та директрисою. Вісь
проходить через фокус перпендикулярно
до директриси і додатній напрямок
задається від директриси до фокуса.
Початок координат помістимо посередині
між фокусом та директрисою. Вісь спрямовується так, щоб система
спрямовується так, щоб система була правою. (Рис. 42.1)
була правою. (Рис. 42.1)
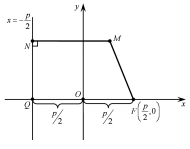
Рис. 42.1
При
такому виборі системи координат якщо
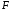 - фокус параболи, то
- фокус параболи, то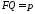 - парамаетр параболи. Тоді фокус має
координати
- парамаетр параболи. Тоді фокус має
координати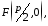 а директриса задається рівнянням
а директриса задається рівнянням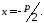
Розглянемо
довільну точку параболи
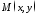 .
З’єднаємо
.
З’єднаємо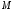 і фокус
і фокус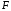 і проведемо
і проведемо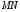 - перпендикуляр до директриси (Рис.
42.1). Знаходимо
- перпендикуляр до директриси (Рис.
42.1). Знаходимо
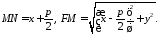
Для
будь-якої точки на параболі має
виконуватись рівність
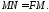 Отже
Отже
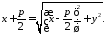
Піднесемо обидві частини останньої рівності до квадрату і здійснимо перетворення:
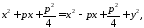
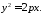 954295\* MERGEFORMAT (.)
954295\* MERGEFORMAT (.)
Рівняння 4295 називається канонічним рівнянням параболи.
Рівняння 4295 дозволяє встановити такі властивості параболи.
Оскільки
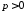 і
і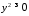 ,
то з 4295 випливає, що
,
то з 4295 випливає, що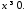 Отже, парабола- необмежена крива, що
знаходиться у правій півплощині
координатної площини
Отже, парабола- необмежена крива, що
знаходиться у правій півплощині
координатної площини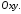
Точка
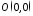 належить парболі і називаєтьсявершиною
параболи.
належить парболі і називаєтьсявершиною
параболи.Для кожної точки параболи
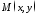 симетрична відносно осі
симетрична відносно осі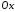 точка
точка теж належить до параболи. Отже вісь
теж належить до параболи. Отже вісь - вісь симетрії параболи. Центра симетрії
парабола не має.
- вісь симетрії параболи. Центра симетрії
парабола не має.
Властивості 1 – 3 досволяють зобразити параболу (Рис. 42.2):
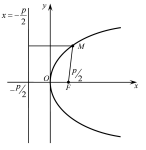
Рис. 42.2
У
данній системі координат
 можно розглянути ще три параболи з
вершиною у точці
можно розглянути ще три параболи з
вершиною у точці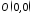 ,
параметром
,
параметром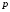 і осями симетрії, які співпадають з
координатними осями:
і осями симетрії, які співпадають з
координатними осями:
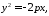 фокус
фокус
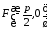 ,
директриса
,
директриса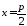
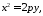 фокус
фокус
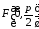 ,
директриса
,
директриса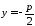
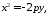 фокус
фокус
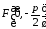 ,
директриса
,
директриса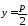 .
.
9643Equation Section (Next)§ 43. Складання і дослідження канонічних рівнянь кривих другого порядку
Задача 43.1. Скласти рівняння еліпса, фокуси якого розташовані на осі абсцис симетрично щодо початку координат, якщо відомі:
1)
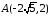 –точка
на еліпсі та
–точка
на еліпсі та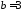 –
мала піввісь;
–
мала піввісь;
2)
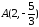 –
точка на еліпсі,
–
точка на еліпсі,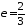 –
ексцентриситет.
–
ексцентриситет.
Розв’язання.
