
- •Розділ II. Елементи аналітичної геометрії
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •1) Підставимо в канонічне рівняння еліпса 4078 замість такоординати точкиА, а також дане значення . Одержимо рівняння:.
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •§ 48. Розв’язування задач на складання рівнянь поверхонь та їх дослідження
- •Задачі для самостійної роботи
- •Питання для повторення
- •Відповіді
- •Додаток
- •Програма модульного контролю з теми
- •Лінійна і векторна алгебра
- •Теоретичні запитання.
- •Зразки практичних завданнь.
- •Програма модульного контролю з теми аналітична геометрія Теоретичні запитання.
- •Зразки практичних завдань.
- •Література.
Задачі для самостійної роботи
Записати параметричне рівняння прямої, що проходить через точку
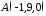 паралельно вектору
паралельно вектору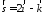 .
.Скласти рівняння прямої, що проходить через точку
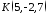 паралельно прямій
паралельно прямій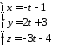 .
.Перевірити, чи лежать на одній прямій точки
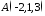 ,
,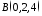 ,
,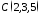 .
.Знайти кут між прямими
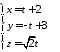 та
та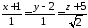 .
.Скласти канонічні та параметричні рівняння прямих:
а)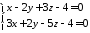 б)
б)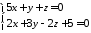
Показати, що прямі
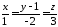 та
та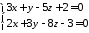 перпендикулярні.
перпендикулярні.Знайти відстань між паралельними прямими
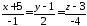 та
та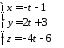
При якому значенні
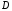 пряма
пряма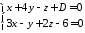 перетинає вісь
перетинає вісь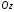 ?
?
Питання для повторення
Різні вигляди рівняння прямої у просторі.
Відстань від точки до прямої
Взаємне розміщення прямих .Кут між прямими.
4334Equation Section (Next)§34. Взаємне розміщення прямої і площини
Розглянемо
деяку площину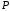 і
пряму
і
пряму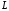 ,
які у системі координат
,
які у системі координат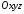 задаються
рівняннями
задаються
рівняннями
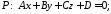
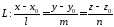 .
.
Пряма може бути паралельною до площини, належати до неї або перетинати.
Якщо
пряма паралельна до площини, то вектори
 і
і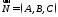 перпендикулярні (Рис.34.1)
перпендикулярні (Рис.34.1)
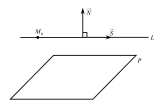
Рис.34.1
Тоді наступна умова є умовою паралельності прямої до площини
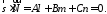 443444\* MERGEFORMAT (.)
443444\* MERGEFORMAT (.)
Коли
пряма належить площині, то точка
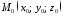 є точкою площини і має задовольняти її
рівняння:
є точкою площини і має задовольняти її
рівняння:
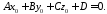 453445\* MERGEFORMAT (.)
453445\* MERGEFORMAT (.)
Тому умовою належності прямої до площини є одночасне виконання рівностей 3444 і 3445.
Коли
умова 3444 порушується, то пряма перетинає
площину під деяким кутом. Нехай
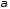 -
гострий кут нахилу прямої до площини
(Рис.34.2)
-
гострий кут нахилу прямої до площини
(Рис.34.2)
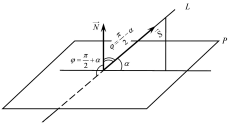
Рис.34.2
Тоді
кут
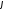 між векторами
між векторами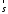 і
і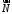 дорівнює
дорівнює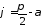 або
або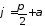 .
Тоді
.
Тоді
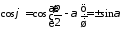 ,
,
або
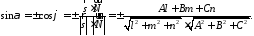 463446\* MERGEFORMAT (.)
463446\* MERGEFORMAT (.)
.
Знак
у формулі 3446 обирається так, щоб отримати
додатне значення
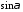 .
.
4735Equation Section (Next)§35. Задачі на взаємне розміщення прямої та площини
Задача
35.1.
Скласти
рівняння площини, що проходить через
точку
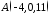 перпендикулярно прямій
перпендикулярно прямій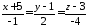 .
.
Розв’язання.
З
умови перпендикулярності прямої і
площини випливає, що за нормальний
вектор площини можна взяти напрямний
вектор прямої:
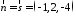 .
.
Тоді рівняння площини має вигляд:
 ,
або
,
або
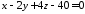 .
.
Задача
35.2.
Знайти кут
між
прямою
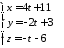 та
площиною
та
площиною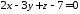 .
.
Розв’язання.
З
даних рівнянь
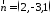 ,
,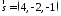 .
Згідно формули 3446 маємо:
.
Згідно формули 3446 маємо:
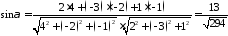 .
.
Задача
35.3.
Знайти точку перетину прямої
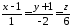 та площини
та площини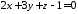 .
.
Розв’язання.
Подамо
рівняння прямої в параметричному
вигляді:
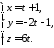
Підставимо
одержані вирази в рівняння площини, щоб
знайти значення параметра
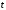 ,
яке відповідає точці перетину прямої
та площини.
,
яке відповідає точці перетину прямої
та площини.
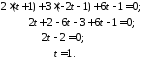
Тепер знайдемо координати точки перетину М:
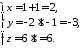
Отже,
точка перетину
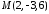 .
.
Задача
35.4.
Показати,
що пряма
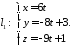 паралельна площині
паралельна площині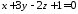 ,
а пряма
,
а пряма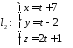 лежить
в цій площині.
лежить
в цій площині.
Розв’язання.
Підставимо
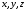 прямої
прямої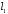 в рівняння площини:
в рівняння площини:
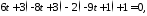
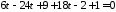 ,
,
тобто
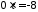 ;
;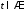 ,
,
і точок перетину пряма та площина не мають.
Отже,
пряма
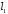 паралельна площині.
паралельна площині.
Здійснивши
аналогічні перетворення з
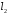 ,
отримаємо
,
отримаємо
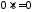 ,
,
що
виконується для будь-якого параметра
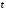 ,
отже,
,
отже,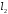 належить
площині.
належить
площині.
Задача
35.5.
При
якому
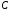 пряма
пряма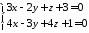 паралельна площині
паралельна площині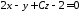 ?
?
Розв’язання.
Нормальний
вектор площини має координати
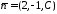 .
Щоб знайти напрямний вектор заданої
прямої, обчислимо векторний добуток
векторів
.
Щоб знайти напрямний вектор заданої
прямої, обчислимо векторний добуток
векторів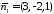 та
та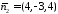 ,
нормальних для двох площин, рівняння
яких містяться у системі.
,
нормальних для двох площин, рівняння
яких містяться у системі.
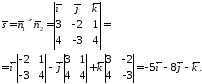
Згідно умові паралельності прямої і площини 3444 знайдемо скалярний добуток:
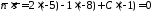 .
.
З одержаного рівняння знайдемо С.
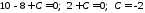 .
.
Задача
35.6.
Скласти рівняння площини яка проходить
через точку
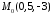 паралельно прямим
паралельно прямим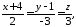
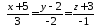 .
.
Розв’язання.
Оскільки дві прямі паралельні шуканій площині, то нормальним до площини є вектор
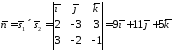 .
.
Знаючи координати нормального вектора та точки площини, складемо рівняння площини:
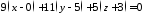 ,
тобто
,
тобто
 .
.
Задача
35.7.
Знайти точку
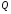 ,
симетричну точці
,
симетричну точці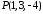 відносно площини
відносно площини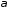 :
: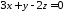 .
.
Розв’язання.
Зобразимо рисунок.

Рис.35.1
Спочатку
складемо рівняння прямої
 ,
яка проходить перпендикулярно заданій
площині через точку
,
яка проходить перпендикулярно заданій
площині через точку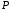 (Рис.35.1).
Нормальний вектор площини
(Рис.35.1).
Нормальний вектор площини
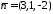 буде одночасно напрямним вектором
прямої, тому її рівнянням є
буде одночасно напрямним вектором
прямої, тому її рівнянням є
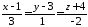 .
.
Тепер
знайдемо точку
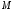 –
проекцію точки
–
проекцію точки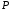 на площину. Це точка перетину прямої та
площини. Запишемо параметричне рівняння
прямої.
на площину. Це точка перетину прямої та
площини. Запишемо параметричне рівняння
прямої.
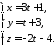
Підставимо
одержані вирази в рівняння площини, щоб
знайти значення параметра
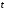 ,
яке відповідає точці перетину прямої
та площини.
,
яке відповідає точці перетину прямої
та площини.
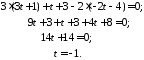
Знайдемо координати точки М.

.
Отже,
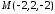
Для
знаходження координат точки
 скористаємось формулами координат
середини відрізку (точкаМ
є серединою
скористаємось формулами координат
середини відрізку (точкаМ
є серединою
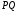 ).
).
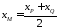 ,
тоді
,
тоді
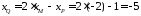 .
.
Аналогічно
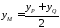 ,
тоді
,
тоді
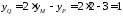 ;
;
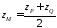 ,
тоді
,
тоді
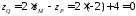 .
.
Значить,
симетрична точка має координати
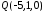 .
.
