
Diplomne_ta_kursove_proektuvannya_UKR
.pdf
або δ = 6 10−3 м. |
|
|
|
|
|
|
|
|
|
|
Одержимо: |
С6 |
= |
4D5b5τ5 sinα5 |
≥ 0,75 |
7.10. |
|||||
|
С |
2 |
− d |
2 |
) |
C0 |
|
|
||
|
5 |
|
(D0 |
|
|
C6 |
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
де C0 C6 =1,02-1,05 це співвідношення характеризує поворот потоку від
радіального до осьового напрямку.
Радіус кривизни середньої лінії лопаток ЗНА:
|
|
1 |
− |
|
D |
2 |
||
|
|
|
D |
|
||||
|
|
|
|
|
|
6 |
|
|
R |
л |
= |
|
|
|
5 |
|
D |
|
|
|
|
|
||||
|
|
|
|
|
|
5 |
||
|
|
|
|
4cosα5 |
||||
Радіус розміточної окружності:
|
|
|
|
|
|
|
|
|
|
R |
= D |
Rл |
|
Rл |
−cosα |
|
+ 0, 25 . |
||
D |
|
D |
5 |
||||||
o |
5 |
|
|
|
|||||
|
|
5 |
|
5 |
|
|
|
|
|
Лопатки ЗНА окреслюють по дузі окружності одного радіуса або частіше по дузі окружності у вхідній частині й по прямій (починаючи з радіуса R 6 ) спрямованій по радіусу, у вихідній ділянці. Радіус ρ яким окреслюється лопатка визначається по формулі:
ρ = |
R2 |
− R2 |
|
||
5 |
6 |
|
7.11. |
||
D cosα |
5 |
||||
|
|
||||
|
5 |
|
|
||
Початкова окружність, на якій перебувають центри дуг лопаток, має
радіус R0 = 
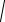 ρ2 − R62 .
ρ2 − R62 .
Результати розрахунків ЗНА представлені в табл.7.1
31
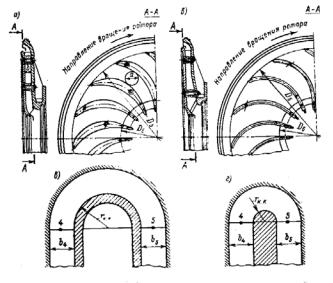
Рис.7.2. Профілювання каналів ЗНА: а - лопатки змінної товщини, бічні стінки - конічні; б - лопатки постійної товщини, зовнішня бічна стінка - профільована; в - кільцеве коліно з більшим
радіусом r к.к ; м – кільцеве коліно з малим радіусом r к.к
8.Равлик (Улітка)
Призначення вихідного пристрою в кінцевому щаблі полягає в тому, що б зібрати газ, що виходить по окружності D 4 з дифузора, і направити його
в нагнітальний трубопровід або за межі проточної частини корпуса для проміжного охолодження.
Вихідні пристрої кінцевого щабля по конструкції можуть бути розділені на 2 типи:
1)спіральні камери (равлики), що характеризуються збільшенням перетинів зі зростанням кута охвата;
32
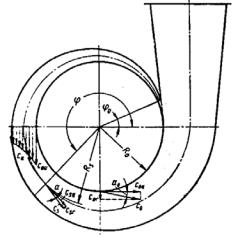
2) кільцеві камери, що мають постійний перетин уздовж вихідної окружності.
Рис. 8.1. Спіральний равлик
Найпростіші спіральні камери виконуються в меридіональному перетині симетричними щодо лінії, що проходить через середину
ширини b 4 нормально до осі обертання ротора. Найбільш часто
зустрічаються форми перетину: трапецієподібна, прямокутна й кругова. Перетини можуть бути розташовані асиметрично. Крім
спіральних камер, зовнішні радіуси r к яких зростають (рис. 8.2 б,в) зі збільшенням кута охвата θ , застосовуються також так звані внутрішні равлики (рис. 8.2 г), у яких r к =const, а збільшення площі перетину зі збільшенням θ досягається зменшенням внутрішнього радіуса r вн .
33
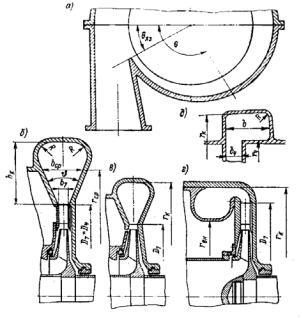
Рис.8.2. До розрахунку равлика: а - радіальний перетин равлика;
б- равлик після лопаткового дифузора;
в- бездифузорний равлик; г - внутрішній равлик;
∂- прямокутний равлик
Равлик є різновид безлопаткового дифузора й тому до плину газу в ньому застосовні ті ж рівняння енергії й руху, що й до плину газу в дифузорі такого типу. Звичайно дифузорний ефект у равликах стаціонарних машин невеликий у зв'язку з невеликою зміною швидкостей у них, так що часто вважають питомий об`єм газу незмінним. Якщо не враховувати тертя, то момент кількості руху газу
в равликах залишається постійним; окружна складова швидкості си міняється за законом постійної циркуляції RСu = RоCоu = const .
Розподіл швидкостей си у поперечному перерізі має гіперболічний характер (рис. 8.1.).
34

Радіальна складова швидкості сr при незмінному питомому об`ємі газу для симетричних равликів (у яких осьова ширина залежить тільки від радіуса й на даному радіусі не залежить від кута повороту ϕ ) округляється на будь-якому поточному радіусі з рівняння:
|
C r = C0r |
R0 |
b0 |
8.1. |
|
R |
b |
||
де R 0 |
- початковий радіус равлика |
|
|
|
C0r - радіальна складова швидкості на R0 |
|
|||
b 0 |
і b – ширина равлика в поперечному перерізі на радіусах |
|
||
R0 і R.
В останні роки одержали широке поширення внутрішні равлики. Вони дозволяють зменшити діаметральні розміри компресора, а
асиметричний плин потоку в них дозволяє зменшити втрати енергії. Прикладом такого равлика є кільцева (див. рис. 8.3).
При визначенні геометричних розмірів равлика варто керуватися наступними рекомендаціями:
1)b 5 > b4 , орієнтовно b5 =1,3b4 ;
2)равлик має прямокутний перетин, отже b=bcр ,а кs = 1,18;
bср = |
|
2πb4 Ks tgα4 |
|
|
|
= 3.22b4 |
tgα4 |
|
або |
||||||||||||||
2,303 ∂ (Dk D |
|
) |
|
∂ (Dk D |
) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
вн |
|
|
|
|
|
|
|
вн |
|||
|
bcp |
= (0,1−0,15)D4 |
|
|
|
|
|
|
|
|
|
|
8.2. |
||||||||||
|
bср |
|
|
|
6, 44(b4 D |
)tgα4 |
|
|
|
|
|
|
|
||||||||||
|
|
|
= |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
8.3. |
||
|
h |
|
(1 |
− D |
k |
D )lg(D |
D ) |
|
|
||||||||||||||
|
kвн |
|
|
k |
|
|
|
вн |
|
|
|
|
|
|
|
|
|
|
|
|
|||
R вн = |
|
|
|
|
|
Rk |
|
|
|
|
|
|
|
|
|
|
|
8.4. |
|||||
exp( |
|
|
|
Vpθ |
|
|
|
|
|
) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
360K |
v4 |
C |
u |
4 |
R b |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
ср |
|
|
|
||||||
35
|
Kv4 = |
v ′′ |
|
|
||
де |
1 |
, C u4 = C4 cosα4 |
|
|
||
|
|
v4 |
|
|
|
|
v p = 0.85G0 v1" |
8.5. |
|||||
Результати розрахунків равлика представлені в табл. 8.1 |
||||||
|
|
Лопатковий дифузор |
Таблиця 6.1 |
|||
|
|
|
|
|
|
|
Параметр |
|
Щабель |
|
|
||
|
|
|
|
|
|
|
|
|
|
I |
|
II |
|
|
|
|
|
|
|
|
D 3 |
, м |
|
0,55 |
|
0,55 |
|
С4 |
, м/с |
|
48,092 |
|
39,5 |
|
' |
, м/с |
|
154,77 |
|
- |
|
С2 |
|
|
|
|
|
|
α2' , град |
|
15,2 |
|
15,0 |
|
|
b 3 |
, м |
|
0,039 |
|
0,016 |
|
K д |
|
3,218 |
|
- |
|
|
− |
|
|
1,492 |
|
1,42 |
|
D4 |
|
|
|
|
|
|
α3 , град |
|
17,3 |
|
18 |
|
|
|
|
|
|
|
|
|
α4 , град |
|
28,6 |
|
28 |
|
|
Z 3 , шт |
|
16 |
|
20 |
|
|
|
|
|
|
|
|
|
υ , град |
|
8,65 |
|
7,96 |
|
|
D f |
|
2,184 |
|
2,061 |
|
|
|
|
|
|
|
|
|
R лд , м |
|
0,489 |
|
0,485 |
|
|
R 0 |
, м |
|
0,241 |
|
0,239 |
|
36
|
ЗНА |
Таблиця 7.1 |
||
|
|
|
|
|
Параметр |
|
Значення |
||
|
|
|
|
|
b 5 |
, м |
|
0,041 |
|
|
|
|
|
|
α5 , град |
|
31,61 |
|
|
D 5 |
, град |
|
0,76 |
|
|
|
|
|
|
b 6 |
, м |
|
0,049 |
|
|
|
|
|
|
D 6 |
, м |
|
0,258 |
|
|
|
|
|
|
Z 5 , шт |
|
12 |
|
|
τ6 |
|
|
0,901 |
|
|
|
|
|
|
R л |
, м |
|
0,296 |
|
R 0 |
, м |
|
0,200 |
|
r кл |
|
|
0,063 |
|
|
|
|
|
|
|
|
|
|
|
Равлик |
|
|
|
|
|
|
Таблиця 8.1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Параметр |
b |
ср |
V |
р |
V н |
|
Сu 4 |
К v |
R k |
R |
4 |
|
|
|
|
R |
|
|
, м |
|
|
|
||||
м |
|
м |
3 |
/с |
м |
2 |
/с |
м/с |
м |
м |
|
|
|
|
|
вн |
|
|
|
|||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
22, |
45 |
90 |
135 |
|
180 |
|
225 |
270 |
315 |
|
град |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0,085 |
0,64 |
|
|
0,48 |
|
27,6 |
6,25 |
0,436 |
|
0,373 |
|
0,436 |
0,433 |
0,43 |
0,423 |
0,417 |
|
|
0,411 |
|
0,405 |
0,399 |
0,394 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37
9.Думис
9.1.Визначення осьових зусиль, що діють на ротор відцентрової компресорної секції
Розрахунку основних зусиль передує ескізна розробка поздовжнього розрізу проточної частини: вала з робочими колісьми, діафрагм із дифузорами й ЗНА і елементів корпуса. У результаті визначаються діаметри покришечних лабіринтових ущільнень і діаметри ущільнень вала біля робочих дисків коліс. Тиск перед робочим колесом і за ними визначається з газодинамічного розрахунку проточної частини. Наприклад, у паровому відцентровому компресорі тиск перед колесами й за ними визначається за графіком процесу стиску (залежності тиску від єнтальпії): за значеннями єнтальпії перед
колесом i 0 і за колесом i 2 перебувають тиски p0 і p2 .
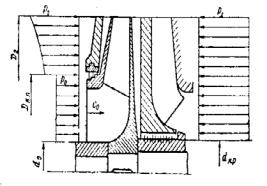
При розрахунку осьового зусилля можна прийняти наступну схему розподілу тиску уздовж радіуса по дисках.
У покриваючих дисків тиск по радіусі завжди змінюється по параболічній залежності.
Рис.9.1. Схема розподілу тисків навколо робочого колеса
щабля зі зворотним напрямним апаратом |
|
Для робочих дисків можливі 2 випадки. |
|
1) Тиск за колесом p 2 нижче, ніж тиск перед ущільненням |
вала |
при вході в наступне робоче колесо, а перепад тиску в цьому ущільненні
38
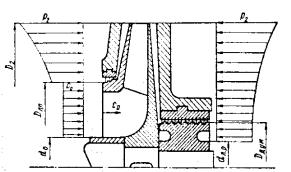
спрямований убік робочого диска розглянутого колеса. Тоді тиск біля
робочого диска |
може бути прийнято постійним по радіусі й рівним тиску |
за колесом p 2 |
. Цей випадок характерний для щаблів пром іжного типу, |
що мають ЗНА (рис.9.1.) |
|
2) Тиск за колесом p2 вище, ніж тиск за ущільненням вала, а перепад |
|
тиску в ущільненні біля робочого диска спрямований від диска. У цьому випадку тиск у робочого диска змінюється уздовж радіуса по параболічній залежності, такій же як і біля покриваючого диска. Цей випадок характерний для останнього щабля компресора (рис.9.2.)
Рис.9.2. Схема розподілу тисків навколо колеса кінцевого щабля
При використанні такої розрахункової схеми зусилля, що діє на колесо першого щабля, обчислюється по рівнянню:
|
|
π |
(D2 |
−d2 |
) p + |
π |
(D2 |
− D2 |
) |
u2 |
|
D2 |
+ D2 |
π |
(D2 |
−d2 ) p −GC |
|
||
F |
= |
|
|
2 |
|
2 |
|
л.п |
− |
|
0 |
||||||||
|
Iл п |
4 |
л р . |
. |
2 |
4 л п2 |
. |
|
8v |
|
2D2 |
л п |
4 |
. |
0 0 |
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
9.1.
Всі вхідні в це рівняння величини приймаються по єскізам проточної частини й відповідно до газодинамічного розрахунку компресора.
Осьове зусилля, що діє на колесо другого щабля (ступені другого типу), визначається по рівнянню:
39
|
|
π |
|
2 |
|
2 |
|
|
u22 |
|
Dл2..п |
+dл2.. р |
|
|
π |
|
2 |
|
2 |
|
|
|
|
= |
|
(D |
|
−d |
|
) |
p − |
|
1− |
|
|
) |
− |
|
(D |
|
−d |
|
) p −GC |
|
|
F |
IIл п 4 |
л р.. |
|
.. |
|
[ 2 |
8v |
( |
2D2 |
|
]л п 4 .. |
|
0 |
0 |
0 |
9.2. |
||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
9.2.Визначення розмірів розвантажувального поршня (думіса)
Якщо осьове зусилля, що діє на робочі колеса, повинне сприйматися завзятим підшипником, то цей підшипник може виявитися зайво громіздким і механічні втрати в ньому будуть великими. Зменшення осьового зусилля, сприйманого завзятим підшипником, може бути забезпечено за рахунок застосування думіса. Однак перш ніж розраховувати думіс, доцільно зробити підбір завзятого підшипника й оцінити осьове зусилля, що він може сприйняти.
Крутний момент відповідної внутрішньої потужності N i = G0 ∂
кВт і частоті обертання ротора n визначиться рівнянням: |
|
|||
M i = 9560 |
Ni |
, н. м |
9.3. |
|
n |
||||
|
|
|
||
Приймаючи величину напруги на крутіння в найбільш тонкому
конусі валу під сполучною муфтою τкр |
= 50 106 Па, |
||||
діаметр кінця вала: |
|
||||
|
|
|
|
|
|
d= 3 |
M i |
9.4. |
|||
0.2τкр |
|
|
|||
Округлимо d до кратного 5, наприклад d=0,035 і приймемо діаметр шийок вала, в опорних підшипниках d оп = d + ∆ , наприклад 0.045м
тоді внутрішній діаметр колодок завзятого підшипника приймається рівним 0.05м. Для підшипника з висотою завзятих колодок
b=0.035d уп і центральним |
кутом колодок θ = 300 |
сприймане |
|
підшипником осьове зусилля: |
|
|
|
P=0,7 |
Z |
сd 2 t ρ ∆ |
9.5. |
|
|
kуп |
|
40
