2. Определение момента инерции маховика по заданному коэффициенту неравномерности движения

2.1 Исходные данные

Ход ползуна Е Н_Е = 60мм

Расстояние между стойками L = 150мм

Длина коромысла и шатуна l_CD = l_CE = 170 мм

Коэффициент средней скорости К = 1,2

Координаты центров масс звеньев 3 и 4

lDS₄ = 0,4l_DC (2.1)

lcs₅ = 0,3l_CE (2.2)

Массы звеньев механизма

m₄ = 100кг, m₅ = 95кг, m₆ = 200кг

Сила полезного сопротивления

F_ПС = 25 кН = 25000 Н

Моменты инерции звеньев

Is₄ = 2910^2кгм²

Is₅ = 2810^2кгм²

Угол крайнего правого положения

звена 4  = 6º

Коэффициент неравномерности движения

 =0,05

Частота вращения кривошипа

n₁ = 75 мин^-1

Синхронная частота вращения электродвигателя

n_С = 1500 мин^-1

2.2 Синтез кинематической схемы рычажного механизма

Принимаем масштаб построения М 1:1 и строим крайние положения звена 3 определяемые углом  = 6º и ходом ползуна Е ( Н_Е = 60 мм ), см. рис. 2.3

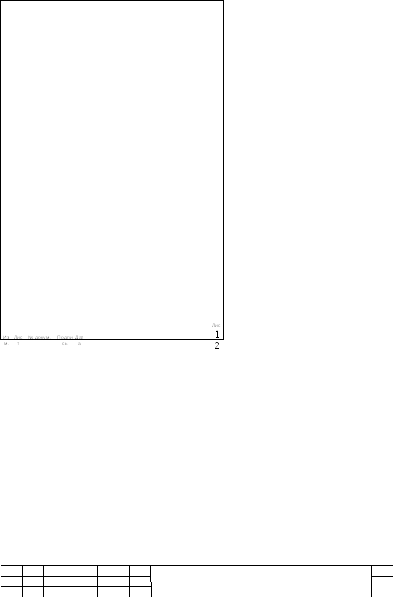
Соединяем точки С_Н и С_К отрезком. Определяем угол  по формуле

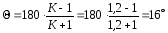(2.3)

От отрезка ( С_НС_К ) в точке С_Н отстраиваем луч под углом

90  = 90º 16º = 74º

В равнобедренном треугольнике С_НDС_К проводим медиану из вершины D и продолжаем её до пересечения с лучом в точке О.

На расстоянии L = 150 мм от точки D проводим вертикаль. Из точки С_Н проводим дугу с центром в точке О до пересечения её с вертикалью в точке А.

Измерением находим отрезки ( учитывая масштаб построения )

АС_Н= 277 мм

АС_К= 227 мм

Из системы уравнений

Находим длины звеньев

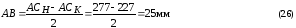
ВС = АСК + АВ = 227 + 25 = 252мм (2.7)

Определяем положения центров тяжести звеньев 3 и 4 по зависимостям (2.1) и (2.2)

lDS₄ = 0,4l_DC = 0,4170 = 68 мм

lcs₅ = 0,3l_CE = 0,3130 = 51 мм

2.3 Построение плана положений механизма

Методом засечек строим план механизма в 6-ти положениях, соответствующих 6 равноотстоящим положениям кривошипа. Принимаем длину кривошипа на чертеже (АВ) = 25 мм и определяем масштабный коэффициент плана положений

(2.8)

2.4 Построение планов скоростей

Определяем угловую скорость кривошипа

(2.9)

Скорость точки В:

(2.10)

Принимаем длину вектора, изображающего скорость точки В на планах скоростей (р_vв) = 100 мм и определяем масштабный коэффициент планов скоростей

(2.11)

Скорость точки С определяется системой векторных уравнений

Скорость точки Е определяется векторным уравнением

(2.14)

По записанным векторным уравнениям строим планы скоростей механизма.

Описание построения планов скоростей.

От произвольно выбранной точки p_v – полюса плана скоростей отстраиваем вектор ( p_vв ) длиной 100 мм перпендикулярно звену АВ. Через точку в проводим прямую перпендикулярно звену ВС, а через полюс p_v проводим прямую перпендикулярно звену DC и на пересечении этих двух прямых получаем точку c. Через полюс p_v проводим вертикальную прямую – параллельно направляющей ползуна E, а через точку С проводим прямую перпендикулярную звену CE, и на пересечении этих двух прямых получаем точку e. Это построение выполняем 6 раз для всех расчётных положений механизма.

Из построенных планов скоростей определяем скорости точек и угловые скорости звеньев механизма по формулам:

Для всех положений

V_В=0,2м/с

(р_vв) = 100 мм L_DC= 0,17м

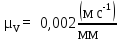L_ЕC= 0,17м

Положение № 1

V_ЕС = (ес)·_v = 0·0,002 = 0м/с

V_С = (p_vс)·_v = 0·0,002 = 0м/с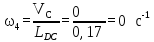

V_S4 = (p_vs₄)·_v = 0·0,002 = 0м/с

V_S5 = (p_vs₅)·_v = 0·0,002 = 0м/с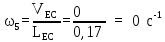

V_Е = V_S6 = (p_vе)·_v = 0·0,002 = 0м/с

Положение №2

V_ЕС = (ес)·_v = 203·0,002 = 0,406м/с

V_С = (p_vс)·_v = 203·0,002 = 0,406м/с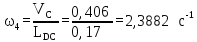

V_S4 = (p_vs₄)·_v = 81·0,002 = 0,162м/с

V_S5 = (p_vs₅)·_v = 170·0,002 = 0,34м/с

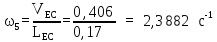
V_Е = V_S6 = (p_vе)·_v = 170·0,002 = 0,34м/с

Положение №3

V_ЕС = (ес)·_v = 114·0,002 = 0,228м/с

V_С = (p_vс)·_v = 114·0,002 = 0,228м/с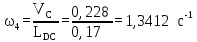

V_S4 = (p_vs₄)·_v = 46·0,002 = 0,092м/с

V_S5 = (p_vs₅)·_v = 82·0,002 = 0,164м/с

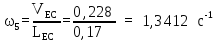
V_Е = V_S6 = (p_vе)·_v = 36·0,002 = 0,072м/с

Положение №4

V_ЕС = (ес)·_v = 37·0,002 = 0,074м/с

V_С = (p_vс)·_v = 37·0,002 = 0,074м/с

V_S4 = (p_vs₄)·_v = 15·0,002 = 0,03м/с

V_S5 = (p_vs₅)·_v = 26·0,002 = 0,052м/с

V_Е = V_S6 = (p_vе)·_v = 8·0,002 = 0,016м/с

Положение №5

V_ЕС = (ес)·_v = 134·0,002 = 0,268м/с

V_С = (p_vс)·_v = 134·0,002 = 0,268м/с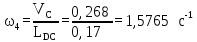

V_S4 = (p_vs₄)·_v = 54·0,002 = 0,108м/с

V_S5 = (p_vs₅)·_v = 100·0,002 = 0,2м/с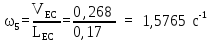

V_Е = V_S6 = (p_vе)·_v = 65·0,002 = 0,13м/с

Положение №6

V_ЕС = (ес)·_v = 146·0,002 = 0,292м/с

V_С = (p_vс)·_v = 146·0,002 = 0,292м/с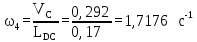

V_S4 = (p_vs₄)·_v = 58·0,002 = 0,116м/с

V_S5 = (p_vs₅)·_v = 126·0,002 = 0,252м/с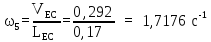

V_Е = V_S6 = (p_vе)·_v = 134·0,002 = 0,268м/с

Результаты всех этих расчётов представляем в таблице 2.1

Таблица 2.1

Длины векторов планов скоростей, скорости точек и угловые скорости звеньев механизма

№ пол.	VB	(pvc)	VC	(ec)	VEC	(pvs4)	VS4	(pvS5)	VS5	(pve)	VE= VS6	4	5
		мм	м/с	мм	м/с	мм	м/с	мм	м/с	мм	м/с	С-1
1		0	0,0	0	0,0	0	0,0	0	0,0	0	0,0	0,0	0,0
2	100 мм	203	0,406	203	0,406	81	0,162	170	0,34	170	0,34	2,3882	2,3882
3	( pvв ) =	114	0,228	114	0,228	46	0,092	82	0,164	36	0,072	1,3412	1,3412
4		37	0,074	37	0,074	15	0,03	26	0,052	8	0,016	0,4353	0,4353
5	0,2 м/с	134	0,268	134	0,268	54	0,108	100	0,2	65	0,13	1,5765	1,5765
6	VB =	146	0,292	146	0,292	58	0,116	126	0,252	134	0,268	1,7176	1,7176

Чтобы определить значения приведённого момента сил сопротивления и сил тяжести нам необходимо определить силы тяжести звеньев, и силу полезного сопротивления.

2.5 Силы тяжести звеньев определим по формуле

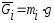(2.22)

где m_i – масса соответствующего звена, кг. (см. п. 2.1 )

g = 9,81 ≈ 10 м/с² – ускорение свободного падения.

G2 = ∙ 10 = H	G5 = 95 ∙ 10 = 950 H
G4 = 100 ∙ 10 = 1000 H	G6 = 200 ∙ 10 = 2000 H