9. 1. Література

1. Капітонова Ю.В., Кривий С.Л., Летичевський О.А., Луцький Г.М., Печорін М.К. Основи дискретної математики. – К.: Наукова думка, 2002. – С.15-18, 30-37.

2. Кужель О.В. Елементи теорії множин і математичної логіки. – К.: Рад. школа, 1977. – С. 26-42.

11. Тема 1.3. Властивості відношень

1.3.1. Теоретико-множинні операції над відношеннями

Оскільки відношення є множинами, елементами яких є впорядковані пари, то над ними можна виконувати всі відомі операції над множинами.

Наприклад, якщо , а , то

;

;

;

.

Якщо відношення “менше”, “більше”, “дорівнює” тощо записати значками для їх позначення у дужках, то операції над цими відношеннями матимуть вигляд:

.

Якщо для двох відношень і виконується умова , то називають розширенням відношення , а – звуженням відношення .

Наприклад, – розширення відношень і , бо і .

1.3.2. Композиція відношень

Крім теоретико-множинних операцій над відношеннями можна виконувати й інші операції. Однією з них є композиція.

Означення 1.3.1. Композицією відношень і називають множину всіх таких впорядкованих пар , для кожної з яких існує деякий елемент такий, що , .

Позначають композицію . Отже, за означенням:

.

Наприклад, якщо , а , то

,

.

Приклад свідчить, що композиція відношень, у загальному випадку, – операція не комутативна, тобто . Однак, композиція має такі властивості:

1. асоціативність: ;

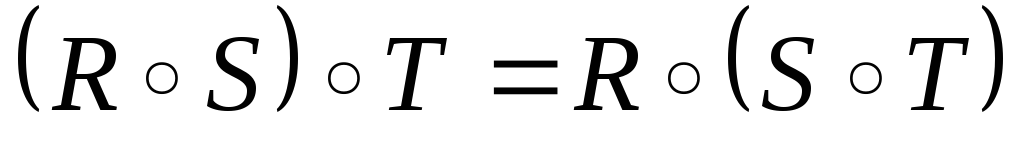2. дистрибутивність відносно : .

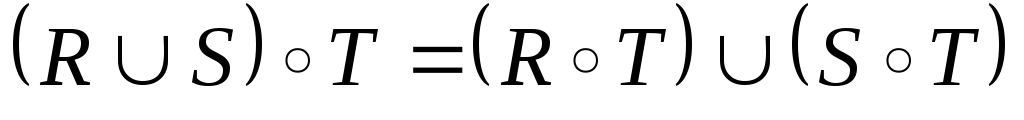1.3.3. Обернені відношення

Означення 1.3.2. Відношення , задане на множині , називають оберненим (інверсним) до відношення , заданого на , якщо

.

Означення 1.3.3. Інверсією називають операцію, яка довільному відношенню ставить у відповідність відношення .

З означення видно, що область визначення відношення є множиною значень для відношення , і навпаки.

Геометричне зображення інверсії графіка легко утворити за допомогою перетворення симетрії координатної площини відносно бісектриси першого координатного кута. При цьому вісь абсцис і вісь ординат міняються місцями, а точка переходить у точку .

Зрозуміло, що у випадку універсального, діагонального та порожнього відношень:

.

Властивості обернених відношень:

1. ;

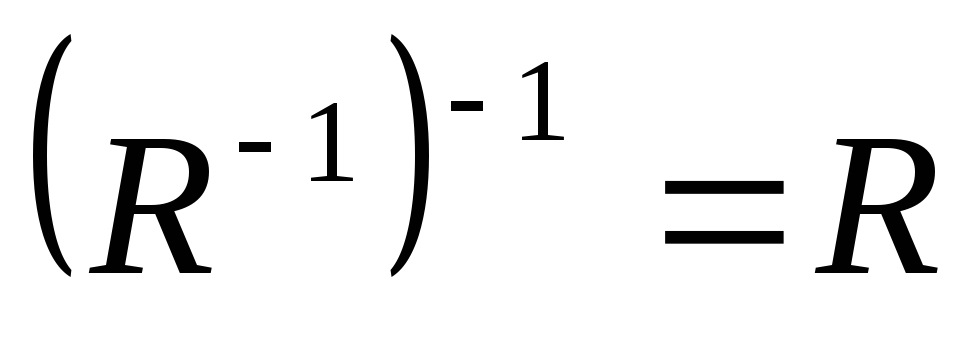2. якщо , то ;

3. ;

4. ;

5. .

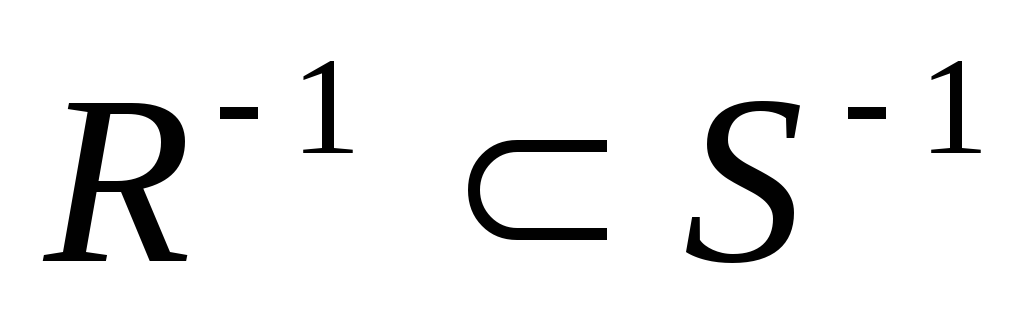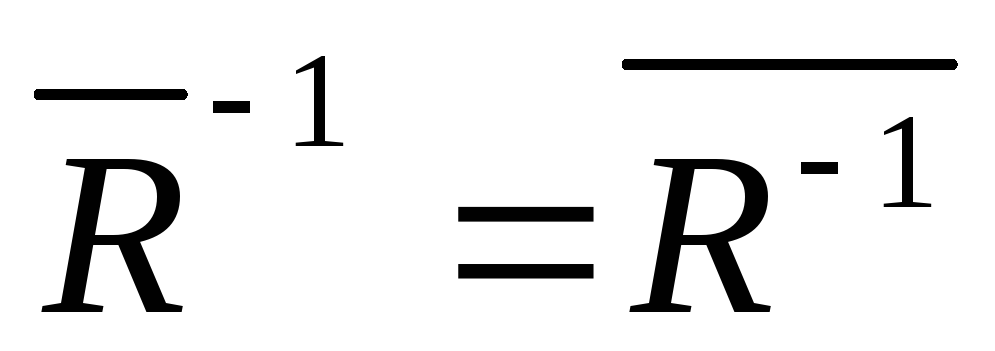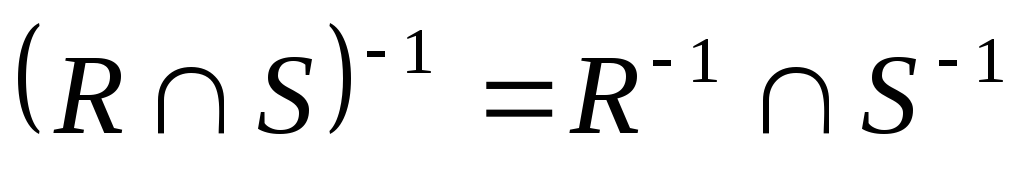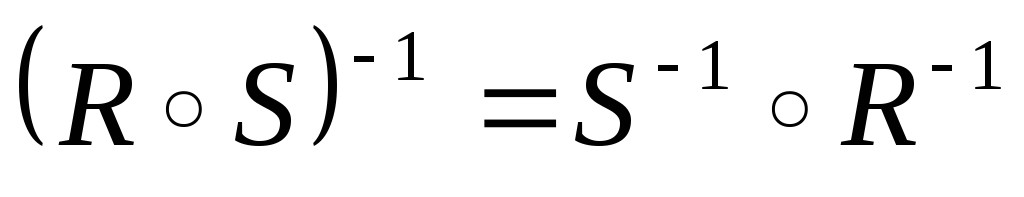1.3.4. Рефлексивні, симетричні і транзитивні відношення

Означення 1.3.4. Бінарне відношення R називають рефлексивним у множині , якщо будь-який елемент перебуває у відношенні сам з собою ().

Означення 1.3.5. Бінарне відношення R називають рефлексивним, якщо з того, що слідує, що і .

Наприклад, відношення рефлексивне у множині , проте не рефлексивне у множині .

Рефлексивними є відношення рівності, подільності, паралельності, конгруентності, подібності фігур, універсальне та діагональне відношення.

Означення 1.3.6. Бінарне відношення R називають антирефлексивним (іррефлексивним) у множині , якщо жоден елемент не перебуває у відношенні сам з собою ().

Наприклад, відношення антирефлексивне у множині . Анти рефлексивними є відношення “не дорівнює”, “менше”, “більше”, перпендикулярності тощо.

Порожнє відношення прийнято вважати як рефлексивним, так і антирефлексивним.

Якщо відношення є ні рефлексивним, ні анти рефлексивним, то його називають не рефлексивним.

Наприклад, відношення не рефлексивне, оскільки елемент 2, на відміну від всіх інших, не перебуває у відношенні сам з собою .

При зображенні рефлексивного відношення з допомогою графіка видно, що всі точки діагоналі належать графіку відношення.

Означення 1.3.7. Бінарне відношення R називають симетричним, якщо з того, що слідує, що .

Наприклад, відношення симетричне. Симетричними є відношення паралельності, перпендикулярності, подібності, конгруентності, універсальне відношення тощо.

Для симетричного відношення його графік симетричний відносно діагоналі – бісектриси координатного кута.

Означення 1.3.8. Бінарне відношення R називають антисиметричним, якщо з того, що слідує, що .

Наприклад, відношення антисиметричне. Антисиметричними є відношення включення, “менше”, “більше”, “менше дорівнює” тощо.

Відношення рівності, діагональне та порожнє вважають як симетричними, так і антисиметричними.

Означення 1.3.9. Бінарне відношення R називають транзитивним, якщо з того, що і слідує, що .

Наприклад, відношення транзитивне. Транзитивними також є відношення “менше”, “більше дорівнює”, подільності, паралельності, подібності, включення, діагональне, порожнє та універсальне відношення тощо.

Не транзитивними є відношення “не дорівнює”, перпендикулярності, належності тощо.

Графік транзитивного відношення має властивість і навпаки.

Операція обернення зберігає 5 властивостей відношень: рефлективність, антирефлексивність, симетричність, антисиметричність і транзитивність.

Означення 1.3.10. Відношення R* називають транзитивним замиканням відношення R на множині А, якщо тоді і тільки тоді, коли у множині А існує послідовність елементів така, що і , , ..., .

Наприклад, нехай – множина точок на площині і , , якщо точки і з’єднані відрізком. Тоді , якщо існує ламана лінія, яка з’єднує точки і .