1.2.4. Переріз відношення. Фактор-множина
Нехай
– деяке відношення у множині
(
)
і
.
Означення
1.2.4. Сукупність всіх таких елементів
,
для яких
,
називають перерізом
відношення
за елементом
.
Позначують
.
За означенням
.
Наприклад,
нехай
і
.
Тоді:
,
,
,
.
Означення
1.2.5. Сукупність всіх перерізів відношення
за елементами множини
називають фактором
або
фактор-множиною
множини
і позначають
.
Отже,
.
Для
розглянутого прикладу
.
Оскільки
за означенням елементами буліана
є підмножини множини
,
то довільна фактор-множина
є підмножиною цього булана:
.
Нехай
– деяке відношення у множині
(
)
і
.
Означення
1.2.6. Перерізом
відношення
за множиною
називають об’єднання всіх перерізів
відношення
за елементами множини
,
тобто
.
Якщо у
розглянутому прикладі покласти
,
то
.
Якщо
,
то
.
1.2.5. Способи задання відношень
1. Множинний спосіб. Оскільки відношення є множиною, елементами якої є впорядковані пари, то його можна задати за допомогою способів задання множин.
Наприклад,
,
.
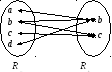
2. Стрілочний спосіб. Елементи області визначення і множини значень відношення зображують точками площини напроти одна від одної, а впорядковані пари зображують стрілками, спрямованими від відповідних точок області визначення до точок множини значень.
Наприклад,
задамо стрілочним способом відношення
,
задане вище множинним способом. Спочатку
знайдемо його область визначення і
множину значень:
,
.
3. Табличний спосіб. Таблиця відношення складається з двох рядків і стількох стовпців, скільки елементів в області визначення. Під кожним елементом області визначення записують переріз відношення за цим елементом.
Наприклад,
задамо стрілочним способом згадане
відношення
.
-
a
b
c
d
{b}
{b,c}
{c}
{b}
4. Матричний спосіб. Матриця відношення має стільки рядків, скільки елементів у області визначення, і стільки стовпців, скільки елементів у множині значень. Елементами матриці відношення є:
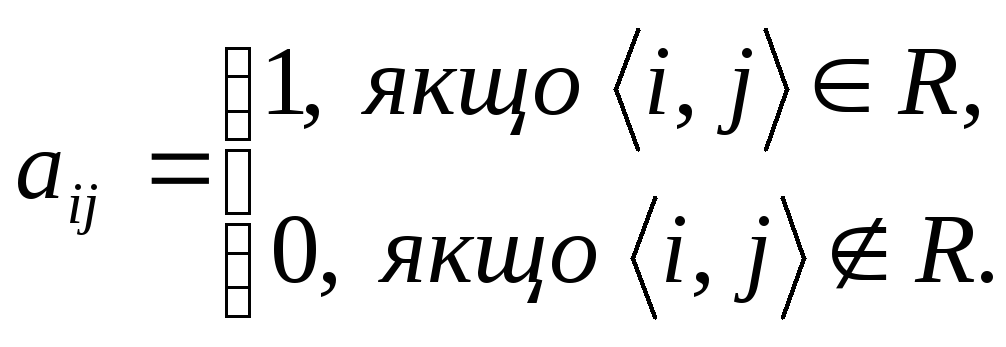
Наприклад,
задамо матричним способом побудоване
раніше відношення
.
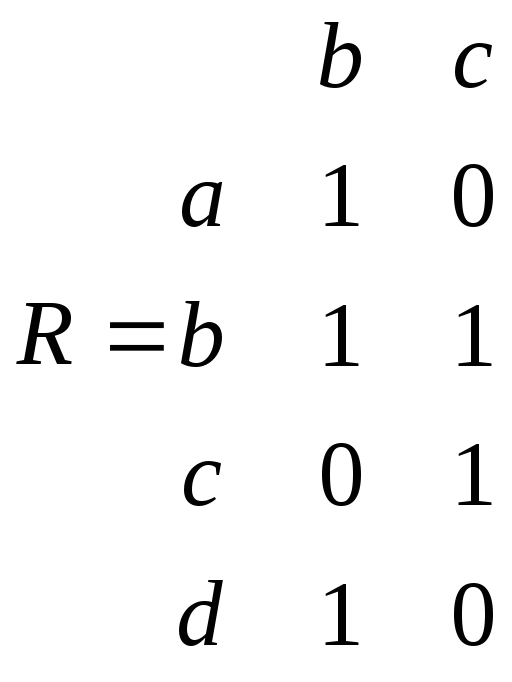
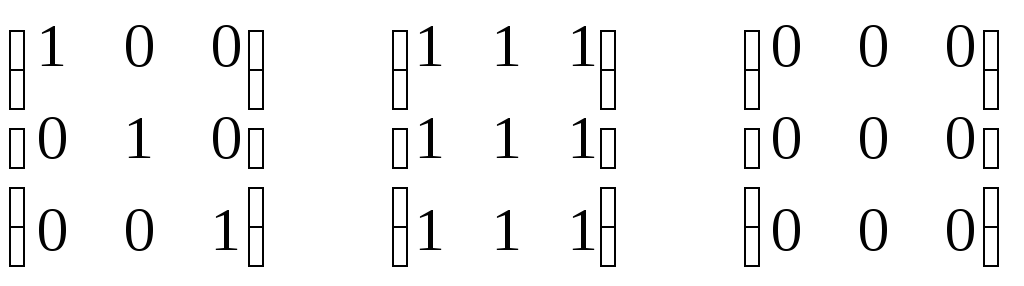
Для
діагонального, універсального та
порожнього відношень у множині
матриці матимуть вигляд:
.
5. Графічний спосіб. Цей спосіб передбачає побудову графіка та графа відношення.
Для побудови графіка у першому координатному куті на горизонтальній осі відкладають точками елементи області визначення, а на вертикальній – точки множини значень. Кожну впорядковану пару зображують точкою або зірочкою у цьому координатному куті (отримані точки не сполучають!).
Для побудови графа відношення елементи поля цього відношення зображують точками довільно на площині. Кожну впорядковану пару зображують дугою, спрямованою від точки області визначення до точки множини значень.
Наприклад,
зобразимо
графічно розглядуване відношення
,
знайшовши його поле:
.
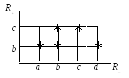
Графік Граф