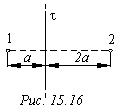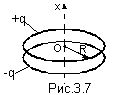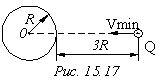1СМ-21_РГЗ

Расчетно-графическое задание № 1

Группа: СМ-21

Студент: 1.

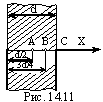
1. Лист стекла толщиной d=2 см. равномерно заряжен с объемной плотностью р=1 мкКл/м**3. Определить напряженность Е и смещение Д электрического поля в т.А,В,С. Построить график зависимости Е(х) (ось Х координат перпендикулярна поверхности листа стекла).

Ответ: Ea=0, Da=0, Eb=80.8 B/m, Db=5 кК/м**2, Ec'=162 B/m, Ec"=1.13 кB/m, Dc=10 нКл/м**2 . рис.3 Рисунок: нет.

2. Тонкая бесконечная нить согнута под углом 90 град. Нить несет заряд, равномерно распределенный с линейной плотностью 1 мкКл/м. Определить силу, действующую на точечный заряд Q =0,1 мкКл, расположенный на продолжении одной из сторон и удаленный от вершины угла на а = 50 см.

Ответ: 4,03 мН. Рисунок: нет.

3. Бесконечно длинная тонкостенная металлическая трубка радиусом 2 см несет равномерно распределенный по поверхности заряд 1 нКл/м**2. Определить напряженность поля в точках, отстоящих от оси трубки на расстояниях 1 см, 3 см.

Ответ: 0;75,5 В/м. Рисунок: нет.

4. Параллельно бесконечной пластине, несущей заряд, равномерно распределенный по площади с поверхностной плотностью 20 нКл/м**2, расположена тонкая нить с равномерно распределенным по длине зарядом (0,4 нКл/м). Определить силу, действующую на отрезок нити длиной 1 м.

Ответ: 452 нН/м. Рисунок: нет.

5. Диполь с электрическим моментом 4 Кл*м свободно установился в поле, созданном бесконечной прямой нитью, заряженной с линейной плотностью 500 нКл/м на расстоянии 10 см от нее. Определить в этой точке величину(dE/dr), характеризующую степень неоднородности поля в направлении силовой линии, и силу, действующую на диполь.

Ответ: 0,9 МВ/м**2; 3,9мкН. Рисунок: нет.

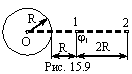
6. Электрическое поле создано отрицательно заряженным металлическим шаром. Определить работу А1,2 внешних сил по перемещению заряда Q=40нКл из точки 1 с потенциалом <фи>1=-300 В в точку 2(рис. 15.9).

Ответ: А= 6 мкДж. Рисунок: 15.9

7. На отрезке тонкого прямого проводника равномерно распределен заряд с линейной плотностью 10 нКл/м. Вычислить потенциал, создаваемый этим зарядом от ближайшего конца отрезка на расстояние, равное длине этого отрезка.

Ответ: 62,4 В. Рисунок: нет.

8. Сплошной парафиновый шар радиусом 10 см равномерно заряжен с объемной плотностью 1 мкКл/м**3. Определить потенциал электрического поля в центре шара и на его поверхности.

Ответ: 472 В; 377 В. Рисунок: нет.

9. Электрическое поле образовано положительно заряженной бесконечно длинной нитью. Двигаясь под действием этого поля от точки, находящейся на расстоянии r1=1 см от нити, до точки r=4 см, АЛЬФА-частица изменила свою скорость от v1=2*10**5 м/с до v2=3*10**6 м/с. Найти линейную плотность заряда ТАУ на нити.

Ответ: ТАУ=3.7 мкКл/м. Рисунок: нет

10. Бесконечно прямая нить несет равномерно распределенный заряд (тау =0.1 мкКл/м). Определить работу А1,2 сил поля по перемещению заряда Q=50 нКл из точки 1 в точку 2.

Ответ: 250 Дж. Рисунок:15.16. Движение заряженных частиц в электрическом поле

11. Электрон с некоторой скоростью влетает в плоский горизонтально расположенный конденсатор параллельно пластинам на равном расстоянии от них. Напряженность поля в конденсаторе E=100 В/м; расстояние между пластинами d=4 см. Через какое время t после того, как электрон влетает в конденсатор, он попадает на одну из пластин? На каком расстоянии s от начала конденсатора электрон попадает на пластину, если он ускорен разностью потенциалов U=60 В?

Ответ: t=480 нс; s=22 см. Рисунок: нет

12. Восемь заряженных водяных капель радиусом r=1 мм и зарядом q=0.1 нКл каждая сливаются в одну общую водяную каплю. Найти потенциал ФИ большой капли.

Ответ: ФИ=3.6 кВ. Рисунок: нет

13. Шар радиусом 1 м заряжен до потенциала 30 кВ. Найти энергию заряженного шара.

Ответ: W=0.05 Дж. Рисунок:нет.

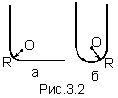
14. Равномерно заряженная нить, на единицу длины которой приходится заряд "лянда", имеет конфигурации показанные на рисунке. Радиус закругления R значительно меньше длины нити. Воспользовавшись результатом решения предыдущей задачи, найти модуль напряженности электрического поля в точке О для конфигураций (а) и (б).

Ответ: а) E="лянда"(2^0.5)/4*"пи"*"эпсилон"o*r; б) E=0. Рисунок: 3.2.

15. Система состоит из двух концентрических проводящих сфер, причем на внутренней сфере радиуса а находится положительный заряд q1. Какой заряд q2 следует поместить на внешнюю сферу радиуса b, чтобы чтобы потенциал внутренней сферы оказался равным нулю ? Как будет зависеть при этом потенциал от расстояния r до центра системы ? Изобразить примерный график этой зависимости.

Ответ: q2=-q1*b/a ; "fi"={q1/(4*"pi"*"эпсилон_0")}*(1/r-1/a) при a<=r<=b "fi"={q1/(4*"pi"*"эпсилон_0")}*(1-b/a)/r при r=>b Рисунок : нет

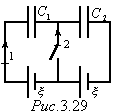
16. В схеме (рис) э.д.с. каждой батареи 'эпсилон'=60 В, емкости конденсаторов С1=2,0 мкФ и С2=3.0 мкФ. Найти заряды, которые пройдут после замыкания ключа К. через течения 1 и 2 в направлениях, указанных стрелками.

Ответ: q1='эпсилон'*C1*(C1-C2)/(C1+C2)=-24 мкКл q2='эпсилон'*(C2-C1)=60 мкКл Рисунок:есть 3.29

17. К источнику с э.д.с. е=100 В подключили последовательно два воздушных конденсатора, каждый емкости С=40 пФ. Затем один из конденсаторов заполнили однородным диэлектриком с проницаемостью е=3.0. Во сколько раз уменьшилась напряженность электрического поля в этом конденсаторе? Какой заряд пройдет через источник?

Ответ: B (e+1)/2=2.0 раза; q=CE(e-1)/2(e+1)=1.0 нКл. Рисунок:нет

18. Плоский конденсатор, расстояние между пластинами которого d=1,0 мм, опустили в горизонтальном положении в воду, которая целиком заполнила его. Затем конденсатор подключили к источнику постоянного напряжения U=500 В. Найти приращение давления воды в конденсаторе.

Ответ: dp='эпсилон'o*'эпсилон'*('эпсилон'-1)*U**2/2*d**2=7kПа =0.7 атм Рисунок: нет

Расчетно-графическое задание № 1

Группа: СМ-21

Студент: 2.

1. Две длинные одноименно заряженные нити расположены на расстоянии r=10см друг от друга. Линейная плотность заряда на нитях лямбда1=лямбда2=10мкКл/м. Найти модуль и направление напряженности Е результирующего электрического поля в точке, находящейся на расстоянии а=10см от каждой нити

Ответ: Е=3.12МВ/м Рисунок: нет.

2. Построить на одном графике кривые зависимости напряженности Е электрического поля от расстояния r в интервале 1<=r<=5см через каждый один см если поле образовано а)точечным зарядом q=33.3нКл б)бесконечно длинной заряженной нитью с линейной плотностью эаряда лямбда=1.67мкКл/м в)бесконечно протяженной плоскостью с поверхностной плотностью заряда Ь=25мкКл/м2

Ответ: Рисунок: нет.

3. Тонкий стержень длиной 10 см равномерно заряжен. Линейная плотность заряда равна 1 мкКл /м. На продолжении оси стержня на расстоянии а = 20 см от ближайшего его конца находится точечный заряд Q = 100 нКл. Определить силу взаимодействия заряженного стержня и точечного заряда.

Ответ: 1,5 мН. Рисунок: нет.

4. Между пластинами плоского конденсатора находится точечный заряд 30 нКл. Поле конденсатора действует на заряд с силой F1=10 мН. Определить силу F2 взаимного притяжения пластин, если площадь S каждой пластины равна 100 см**2.

Ответ: 4,92 мН. Рисунок: нет.

5. Диполь с электрическим моментом 100 пКл*м свободно установился в однородном электрическом поле напряженностью 9 МВ/м. Диполь повернули на малый угол и предоставили самому себе. Определить частоту собственных колебаний диполя в электрическом поле. Момент инерции диполя относительно оси, проходящей через центр диполя, равен 4*10**(-12) кг*м**2.

Ответ: 239 Гц. Рисунок: нет.

6. Две круглые металлические пластины радиусом 10 см каждая, заряженные разноименно, расположены одна против другой параллельно друг другу и притягиваются с силой 2 мН. Расстояние между пластинами равно 1 см. Определить разность потенциалов между пластинами.

Ответ: 1,2 кВ. Рисунок: нет.

7. Заряд распределен равномерно по бесконечной плоскости с поверхностной плотностью 10 нКл/м**2. Определить разность потенциалов двух точек поля, одна из которых находится на плоскости, а другая удалена от плоскости на расстояние 10 см.

Ответ: 56,6 В. Рисунок: нет.

8. Определить потенциал, до которого можно зарядить уединенный металлический шар радиусом 10 см, если напряженность поля, при которой происходит пробой воздуха, равна 3 МВ/м. Найти также максимальную поверхностную плотность электрических зарядов перед пробоем.

Ответ: 300 кВ; 55,6 мкКл/м**2. Рисунок: нет.

9. Пылинка массой 1 пг, несущая на себе пять электронов, прошла в вакууме ускоряющую разность потенциалов 3МВ. Какова кинетическая энергия пылинки? Какую скорость приобрела пылинка?

Ответ: 15 МэВ; 2,19 м/с. Рисунок: нет.

10. Бесконечная тонкая прямая нить несет равномерно распределенный по длине нити заряд с плотностью 1 нКл/м. Каков градиент потенциала в точке, удаленной на расстояние 10 см от нити? Указать направление градиента потенциала.

Ответ: 180 В; градиент направлен к нити вдоль силовой линии. Рисунок: нет.

11. Шар радиусом 6 см заряжен до потенциала 300 В, а шар радиусом 4 см до потенциала 500 В. Определить потенциал шаров после того, как их соединили металлическим проводником. Емкостью соединительного проводника пренебречь.

Ответ: 380 В. Рисунок: нет.

12. Радиус центральной жилы коаксиального кобеля r=1.5 см, радиус оболочки R=3.5 см. Между центральной жилой и оболочкой приложена разность потенциалов U=2.3 кВ. Найти напряженность E электрического поля на расстоянии x=2 см от оси кабеля.

Ответ: E=136 кВ/м. Рисунок: нет

13. Между пластинами плоского конденсатора вложена тонкая слюдяная пластинка. Какое давление испытывает эта пластинка при напряженности электрического поля 10 кВ/см?

Ответ: p=26.5 Па. Рисунок:нет.

14. Очень длинная нить ориентирована перпендикулярно к проводящей плоскости и не доходит до этой плоскости на расстояние l. Нить заряжена равномерно с линейной плотностью "лямбда". Пусть точка О - след нити на плоскости. Найти поверхностную плотность индуцированного заряда на плоскости: а) в точке О; б) в зависимости от расстояния r до точки О.

Ответ: а) "сигма"="лямбда"/2*"pi"*l б) "сигма"(r)="лямбда"/(2*"pi"*[l^2+r^2]^1/2) Рисунок : нет

15. Находящаяся в вакууме круглая тонкая пластинка радиуса R равномерно заряжена с поверхностной плотностью "сигма". Найти потенциал и модуль напряженности электрического поля на оси пластинки как функцию расстояния l от ее центра. Исследовать полученное выражение при l -> 0 и l>>R.

Ответ: "fi"="сигма"*l/{[1+(l/R)^2-1]^1/2}/2*"эпсилон_0" E=("сигма"/2*"эпсилон_0")*(1-l/[l^2+R^2]^1/2) Рисунок : нет

16. Цилиндрический конденсатор заполнен слоями диэлектриков с проницаемостями е1 и е2. Внутренние радиусы слоев равны соответственно R1 и R2>R1. Максимально допустимая напряженность электрического поля для этих диэлектриков равна Е(1m) и Е(2m). При каком соотношении между е, R и Е(m) напряженность поля при повышении напряжения одновременно достигнет значения, соответствующего пробою того и другого диэлектрика?

Ответ: При условии е1R1E(1m)=e2R2E(2m). Рисунок:нет

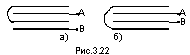
17. Четыре одинаковые металлические пластины расположены в воздухе на расстоянии d=1.00 мм друг от друга. Площадь каждой пластины S=220 см^2. Найти емкость системы между точками А и B, если пластины соединены так, как показана: а) на рис. 3.22, а; б) на рис. 3.22,б.

Ответ: а) С=2е0S/3d=0.13 нФ; б) С=3е0S/2d=0.29 нФ. Рисунок: 3.22, a; 3.22, б.

18. Сферическая оболочка заряжена равномерное поверхностной плотностью 'сигма'. Воспользовавшись законом сохранения энергии, найти модуль электрической силы на единицу поверхности оболочки.

Ответ: F1='сигма'**2/2*'эпсилон'o Рисунок: нет

Расчетно-графическое задание № 1

Группа: СМ-21

Студент: 3..

1. Напряженность электрического поля на оси заряженного кольца имеет максимальное значение на расстоянии L от центра кольца. Во сколько раз напряженность электрического поля в точке расположенного на расстоянии 0.5L от центра кольца будет меньше максимального значения напряженности

Ответ: 1.3 раза Рисунок: нет.

2. АА заряженная вертикальная бесконечная плоскость с поверхностной плотностью заряда b=40мкКл/м2 и B одноименно заряженный шарик с массой м=1г и зарядом q=1нКл. Какой угол а с плоскостью АА образует нить на которой висит шарик.

Ответ: a=13 Рисунок: нет.

3. Тонкое кольцо радиусом 8 см несет заряд, равномерно распределенный с линейной плотностью 10 нКл/м. Какова напряженность электрического поля в точке, равноудаленной от всех точек кольца на расстояние 10 см?

Ответ: 2,71 кВ/м. Рисунок: нет.

4. Две параллельные, бесконечно длинные прямые нити несут заряд, равномерно распределенный по длине с линейными плотностями 0,1 мкКл/м и 0,2 мкКл/м. Определить силу взаимодействия, приходящуюся на отрезок нити длиной 1 м. Расстояние между нитями равно 10 см.

Ответ: 3,6 мН/м. Рисунок: нет.

5. Два диполя с электрическими моментами 20 пКл*м и 50 пКл*м находятся на расстоянии 10 см друг от друга, так что их оси лежат на одной прямой. Вычислить взаимную потенциальную энергию диполей, соответствующую их устойчивому равновесию.

Ответ: 18 нДж. Рисунок: нет.

6. Бесконечно длинная тонкая прямая нить несет равномерно распределенный по длине заряд с линейной плотностью 0,01 мкКл/м. Определить разность потенциалов двух точек поля, удаленных от нити на r1 = 2см и r 2=4 см.

Ответ: 125 В. Рисунок: нет.

7. Две бесконечные параллельные плоскости находятся на расстоянии 1 см друг от друга. Плоскости несут равномерно распределенные по поверхностям заряды с плотностями 0,2 мкКл/м**2 и 0,5 мкКл/м**2. Найти разность потенциалов пластин.

Ответ: 170 В. Рисунок: нет.

8. По тонкому кольцу радиусом 10 см равномерно распределен заряд с линейной плотностью 10 нКл/м. Определить потенциал в точке, лежащей на оси кольца, на расстоянии a = 5 см от центра.

Ответ: 505 В. Рисунок: нет.

9. Электрон влетел в плоский конденсатор, имея скорость 10 Мм/с, направленную параллельно пластинам. В момент вылета из конденсатора направление скорости электрона составляло угол 35 град. с первоначальным направлением скорости. Определить разность потенциалов между пластинами (поле считать однородным), если длина пластин равна 10 см и расстояние между ними равно 2 см.

Ответ: 79,6 В. Рисунок: нет.

10. Положительно заряженная частица, заряд которой равен элементарному заряду, прошла ускоряющую разность потенциалов 60 кВ и летит на ядро атома лития, заряд которого равен 3 элементарным зарядам. На какое наименьшее расстояние частица может приблизиться к ядру? Начальное расстояние частицы от ядра можно считать практически бесконечно большим, а массу частицы - пренебрежимо малой по сравнению с массой ядра.

Ответ: 72фм. Рисунок: нет.

11. На пластинах плоского конденсатора равномерно распределен заряд с поверхностной плотностью 0,2 мкКл/м**2. Расстояние между пластинами равно 1 мм. Определить на сколько изменится разность потенциалов на его обкладках при увеличении расстояния между пластинами до 3 мм?

Ответ: 22,6В. Рисунок: нет.

12. Между пластинами плоского конденсатора находится парафин. При присоединении пластин к источнику напряжения давление пластин на парафин стало равным 5 Па. Найти: 1)напряженность электрического поля и электрическое смещение в парафине, 2) поверхностную плотность связанных зарядов на парафине, 3)поверхностную плотность зарядов на пластинах конденсатора, 4) объемную плотность энергии электрического поля в парафине, 5) диэлектрическую восприимчивость парафина.

Ответ: 1) Е=7.52*10**5 В/м ,D=1.33*10**-5 Кл/м**2; 2) сигма=6.7*10**-6 Кл/м**2. Рисунок:нет.

13. Расстояние между пластинами плоского конденсатора равно 2 см, разность потенциалов 6 кВ. Заряд каждой пластины равен 10 нКл. Вычислить энергию поля конденсатора и силу взаимного притяжения пластин.

Ответ: 30 мкДж. Рисунок: нет.

14. Точечный заряд q=2,00 мкКл находиться между двумя проводящими взаимно перпендикулярными полуплоскостями. Расстояние от заряда до каждой полуплоскости l=5.0 см. Найти модуль силы, действующей на заряд.

Ответ: F=(2*2^1/2-1)*q^2/(32*"pi"*"эпсилон_0"*l^2)=3.3 H Рисунок : нет

15. Два коаксиальных кольца, каждое радиуса R, из тонкой проволоки находятся на малом расстоянии l друг от друга (l<<R) и имеют заряды q и -q. Найти потенциал и напряженность электрического поля на оси системы как функции координаты х (рис 3.7). Изобразить на одном рисунке примерные графики полученных зависимостей. Исследовать эти функции при ¦х¦>>R.

Ответ: "fi"=(ql/4*"pi"*"эпсилон_0")*(x/[R^2+x^2]^3/2) : E_x= -(ql/4*"pi"*"эпсилон_0")*{(R^2-2*x^2)/[R^2+x^2]^5/2} При ¦x¦>>R "fi" =ql/(4*"pi"*"эпсилон_0"*x^2); E_x=ql/(2*"pi"*"эпсилон_0"* *x^3) Рисунок : 3.7

16. Решить предыдущую задачу с тем отличием, что диэлектриком заполнили половину зазора, как показано на рисунке.

Ответ: а) E1=E2=E0,D1=e0E0,D2=eD1; б) E1=E2=2E0/(e+1),D2=eD1. Рисунок:3.17

17. Два длинных прямых провода с одинаковым радиусом сечения а расположены в воздухе параллельно друг другу. Расстояние между их осями равно b. Найти взаимную емкость проводов С1 на единицу их длины при условии b>>а. Вычислить С1,если а=1.00 мм и b=50мм.

Ответ: C1=пие0(ln(b/a))=7.1 пФ/м. Рисунок: нет

18. Конденсатор состоит из двух неподвижных пластин, имеющих форму полукруга радиуса R, и расположенной между ними подвижной пластины из диэлектрика 'сигма' проницаемостью 'эпсилон', которая может свободно поворачиваться вокруг оси О (риc). Толщина подвижной пластины d, что практически равно расстоянию между неподвижными пластинами. Конденсатор поддерживают при постоянном напряжении U. Найти модуль момента сил относительно оси О, действующих на подвижную пластину в положении, на рисунке.

Ответ: N=('эпсилон'-1)*'эпсилон'o*R**2*U**2/4*d, от угла 'альфа' не зависит. Рисунок: есть 3.35

Расчетно-графическое задание № 1

Группа: СМ-21

Студент: 4..

1. Показать что электрическое поле образованное заряженной нитью конечной длинны в предельных случаях переходит в электрическое поле: а)бесконечно длинной заряженной нити, б)точечного заряда.

Ответ: Рисунок: нет.

2. Медный шар радиусом R=0.5см помещен в масло. Плотность масла р=0.8*1000кг/м**3. Найти заряд q шара, если в однородном электрическом поле шар оказался взвешенным в масле. Электрическое поле направлено вертикально вверх и его напряженность Е=3.6 МВ/м.

Ответ: q=11 нКл Рисунок: нет.

3. Полусфера несет заряд, равномерно распределенный с поверхностной плотностью 1нКл/м**2. Найти напряженность электрического поля в геометрическом центре полусферы.

Ответ: 28,3 В/м. Рисунок: нет.

4. На некотором расстоянии а = 5 см от бесконечной проводящей плоскости находится точечный заряд 1 нКл. Определить силу, действующую на заряд со стороны индуцированного им заряда на плоскости.

Ответ: Действие индуцированного заряда эквивалентно действию точечного заряда, являющегося зеркальным изображением заряда Q; 0,9 мкН. Рисунок: нет.

5. Перпендикулярно плечу диполя с электрическим моментом 12 пКл*м возбуждено однородное электрическое поле напряженностью 300 кВ/м. Под действием сил поля диполь начинает поворачиваться относительно оси, проходящей через его центр. Найти угловую скорость диполя в момент прохождения им положения равновесия. Момент инерции диполя относительно оси, перпендикулярной плечу и проходящей через его центр, равен 2*10**(-9) кг*м**2.

Ответ: 6 рад/с. Рисунок: нет.

6. Тонкие стержни образуют квадрат со стороной длиной a. Стержни заряжены с линейной плотностью 1,33 нКл/м. Найти потенциал в центре *квадрата .

Ответ: 33,6 В. Рисунок: нет.

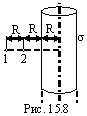
7. Электрическое поле создано бесконечно длинным равномерно заряженным цилиндром радиусом R=5 см. Определить изменение П потенциальной энергии однозарядного положительного иона при перемещении его из точки 1 в точку 2.

Ответ: П=-229 эВ. Рисунок: 15.8

8. Металлический шарик диаметром 2 см заряжен отрицательно до потенциала 150 В. Сколько электронов находится на поверхности шарика?

Ответ: 1,04*10**9. Рисунок: нет.

9. Какой минимальной скоростью должен обладать протон, чтобы он мог достигнуть поверхности заряженного до потенциала <фи>=400 В металлического шара (рис. 15.17)?

Ответ: 0,24 Мм/c. Рисунок: 15.17.

10. Шарик массой м=40мг имеющий положительный заряд q=1нКл движется со скоростью v=10см/с. На какое расстояние r может приблизиться шарик к положительному точечному заряду q0=1.33нКл?

Ответ: r=6см Рисунок: нет.

11. Радиус внутреннего шара воздушного сферического конденсатора r=1 см, радиус внешнего шара R=4 см. Между шарами приложена разность потенциалов U=3 кВ. Найти напряженность E электрического поля на расстоянии x=3 см от центра шаров.

Ответ: E=U*r*R/(R-r)*x**2=44.5 кВ/м. Рисунок: нет_

12. Электрическое поле образовано двумя параллельными пластинами, находящимися на расстоянии d=2 см друг от друга. К пластинам приложена разность потенциалов U=120 В. Какую скорость получит электрон под действием поля, пройдя по линии напряженности расстояние ДЕЛЬТАr=3 мм?

Ответ: v=(2*e*U*ДЕЛЬТАr/m*d)**(1/2)=2.53*10**6 м/с. Рисунок: нет

13. Шар А радиусом 10 см, заряженный до потенциала 3000 В, после отключения источника напряжения соединяется проволокой (емкостью которой можно пренебречь) сначала с удаленным незаряженным шаром В, а затем после отсоединения от В с удаленным незаряженным шаром С. Радиусы шаров С и В равны 10 см. Найти :1) первоначальную энергию шаров А и С, после соединения и работу разряда при соединении.

Ответ: 1) 5*10**-5Дж; 2)1.25*10**-5 Дж и работа2.5*10**-5 Дж; 3)энергия 31.25*10**-5Дж и работа разряда 62.5*10**-5 Дж. Рисунок:нет.

14. Тонкое проволочное кольцо радиуса r=100 мм имеет электрический заряд q=50 мкКл. Каково будет приращение силы, растягивающей проволоку, если в центр кольца поместить точечный заряд qo=7.0 мкКл?

Ответ: "дельта"F=q*qo/8*("пи"**2)*"эпсилон"о*r^2=50 H. Рисунок: нет.

15. Потенциал поля внутри заряженного шара зависит только от расстояния до его центра как "fi"=a*r^2+b, где а и b - постоянные. Найти распределение объемного заряда "ро"(r) внутри шара.

Ответ: "po"=-6*"эпсилон_0"*a Рисунок : нет

16. Определить взаимную емкость системы, которая состоит из металлического шарика радиуса а и безграничной проводящей плоскости, отстоящей от центра шарика на расстояние l, если l>>a.

Ответ: С=4пие0а. Рисунок: нет

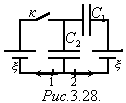
17. Какие заряды протекут после замыкания ключа К и схеме (рис) через сечения 1 и 2 в направлениях, указанных стрелками?

Ответ: q1='эпсилон'*C2 , q2=-'эпсилон'*C1*C2/(C1+C2) Рисунок:есть 2.28

18. Система состоит из двух концентрических тонких металлических оболочек с радиусами R1, R2 и соответствующими зарядами q1 и q2. Найти собственную энергию W1и W2 каждой оболочки, энергию взаимодействия W12 оболочек и полную электрическую энергию W системы

Ответ: W=W1+W2+W12=(q1**2/2*R1+q2**2/2*R2+q1*q2/R2)/ 4*'эпсилон'o*'pi' Рисунок: нет