
- •§1. Предмет і завдання методики початкового навчання математики
- •§2. Методика початкового навчання математики та інші науки -
- •§3. Методи наукового дослідження, що застосовуються в процесі розробки методики викладання початкового курсу математики
- •§4. Освітні, виховні й розвивальні завдання навчання математики в початкових класах
- •§5. Зміст початкового курсу математики. Аналіз програми з математики для початкових класів
- •§6. Математична підготовка дітей в дитячому садку
- •§7. Наступність у навчанні математики між початковими і 5—6 класами
- •§8. Підручник — основний засіб навчання математики в початкових класах
- •§9. Предметне й табличне унаочнення. Використання и структурних схем і малюнків. Дидактичні матеріали
- •16 Кг?, на 20 кг більша
- •§10. Інструменти, прилади й моделі, технічні засоби навчання
- •§11. Засоби зворотного зв'язку
- •§12. Контроль, корекція та закріплення знань учнів
- •Перевірка домашньої роботи
- •Усне опитування
- •Усні обчислення
- •Звичайні приклади
- •Завдання ущільненого характеру
- •Ігри та ігрові форми завдань
- •§13. Методика опрацювання нового матеріалу
- •§14. Закріплення й узагальнення знань учнів
- •Подання домашнього завдання
- •Підсумок уроку
- •Підготовка вчителя до уроку
- •§15. Огляд інших різновидів уроків математики
- •§16. Форми організації навчання учнів математики на уроці
- •§17. Перевірка й оцінювання знань, умінь і навичок учнів з математики
- •Підсумкове оцінювання знань, умінь і навичок
- •§18. Особливості уроку математики в 1 класі
- •§19. Нумерація чисел в межах 10
- •§20. Додавання і віднімання в межах 10
- •§22. Складання та засвоєння таблиць додавання і віднімання з переходом через десяток
- •§24. Усне і письмове додавання та віднімання в межах 100 шд
- •§25. Складання і засвоєння таблиць множення та ділення
- •§26. Нумерація чисел 101-1000
- •§27. Додавання і віднімання в межах 1000
- •§29. Письмове множення і ділення в межах 1000
- •§29. Письмове множення і ділення в межах 1000
- •§30. Методика вивчення нумерації багатоцифрових чисел
- •§31. Додавання і віднімання багатоцифрових чисел
- •§32. Множення і ділення багатоцифрових чисел
- •§33. Вимірювання довжини і площі
- •§34. Ознайомлення з масою тіл
- •§35. Формування часових уявлень в учнів. Ознайомлення з поняттям швидкості
- •§36. Роль і місце задач у початковому курсі математики. Функції текстових задач
- •§37. Складові процесу розв'язування задач
- •§38. Культура запису розв'язань задач
- •§38. Культура запису розв'язань задач
- •§39. Формування навичок розв'язувати прості задачі
- •§39. Формування навичок розв'язувати прості задачі
- •§40. Розвиток уявлень учнів про складену задачу і процес її розв'язування
- •§41. Розв'язування типових задач
- •§42. Розвиток умінь учнів розв'язувати складені задачі
- •§43. Ознайомлення з частинами
- •§44. Ознайомлення з дробами
- •§44. Ознайомлення з дробами
- •§45. Числові вирази. Числові рівності і нерівності. Вирази зі змінною
- •§46. Рівняння. Нерівності зі змінною
- •§47. Формування уявлень учнів про функціональну залежність
- •§48. Розвиток просторових уявлень молодших школярів
- •§48. Розвиток просторових уявлень молодших школярів
- •§49. Формування уявлень про лінії і відрізки
- •§50. Ознайомлення з кругом і многокутником.
- •§51. Математичні ранки
- •III. "Риболови".
- •IV. "Розв'яжи задачу-вірш".
- •§ 52. Математичні олімпіади
- •§ 52. Математичні олімпіади
- •§53. Виховна ефективність уроку математики
- •§54. Планові та стихійно-причинні виховні моменти на уроках математики
- •§55. Перші кроки в створенні методики арифметики. Метод вивчення чисел і метод вивчення дій
- •§56. Початкова математична освіта в 1920—1990 роках
- •§57. Початкова математична освіта в Україні
- •§57. Початкова математична освіта в Україні
- •§1. Предмет і завдання методики початкового навчання математики......................8
§50. Ознайомлення з кругом і многокутником.
Кути многокутника. Прямий кут. Прямокутник.
Периметр многокутника
Зміст роботи розкриємо окремо для кожного класу.
У 1 класі учні ознайомлюються з трикутником, чотирикутником, п'ятикутником і шестикутником. Діти повинні засвоїти правильні назви цих многокутників, вміти їх розпізнавати. З цією метою многокутники, а також круг постійно використовуються як дидактичний матеріал. За програмою розгляд елементів многокутника у 1 класі не передбачено, але багато вчителів у ході аналізу того чи іншого многокутника пропонують показати і полічити сторони, вершини, кути. Таке випередження допустиме, але не слід його вводити в ранг програмових вимог.
У процесі вивчення нумерації чисел першого десятка практикується складання многокутників з паличок, вирізування з паперу, а також розпізнавання многокутників на предметах оточення та малюнках.
Новою вправою буде в цей час розгляд многокутника, поділеного відрізком на дві фігури, і визначення назви кожної фігури (мал. 163).
![]()
Мал. 163
Робота з формування уявлень учнів про круг і многокутники проводиться в тісному зв'язку з уроками праці й образотворчого мистецтва. Діти складають фігури з паперу, малюють їх, використовують фігури для різноманітних аплікаційних робіт, малюють орнаменти з геометричними фігурами.
У 2 класі продовжується робота з формування уявлень учнів про многокутники і круг. Пропонуються дещо ускладнені вправи на розпізнавання многокутників, на поділ фігур на многокутники і немногокутники. Учні вивчають елементи многокутників, вимірюють довжини їх сторін.
Поняття кута і вершини трикутника (многокутника) вводять (конкретизують) за допомогою запитань: Скільки в трикутнику кутів? Вершин? Сторін?
Методика викладання математики в початкових класах
297
Сторони, вершини і кути многокутника потрібно показувати учням на моделях плоских фігур. Кут бажано показати віялоподібним рухом указки, один кінець якої суміщений з вершиною кута многокутника. Треба звернути увагу дітей на те, що вершина многокутника є і вершиною відповідного кута. Бажано показати їм, що кути є різні за величиною, але величина кута не залежить від довжини його сторін.
Прямий кут. Для ознайомлення з прямим кутом варто розглянути його утворення в процесі перегинання листка паперу. Кожному учневі треба дати аркуш паперу довільної форми. Потім під керівництвом учителя діти складають аркуші вдвічі, притискують лінію згину. Після цього аркуш перегинають ще раз, стежачи за тим, щоб частини утвореної раніше лінії перегину сумістилися. Утвориться кут. Такий кут називається прямим. Якщо папір розгорнути, діти побачать, що дві лінії перегину поділяють аркуш на чотири частини. Утворилось чотири прямі кути, які мають спільну вершину.
За допомогою паперової моделі прямого кута учні відшукують прямі і непрямі кути на предметах з навколишнього оточення і на косинці. Після цього користуються прямим кутом косинця.
Прямокутник. Дітям пропонують розглянути малюнки чотирикутників і знайти серед них такі, в яких всі кути прямі (мал. 164). Після цього подають означення прямокутника.

Мал. 164
Варто звернути увагу учнів на форму навколишніх предметів або їх частин. Вони знаходять предмети, що мають форму прямокутника: зошит, книжка, кришка стола, класна дошка тощо.
У процесі вимірювання сторін прямокутника діти встановлюють, що його протилежні сторони рівні.
Через кілька уроків вводять поняття довжини і ширини прямокутника.
Квадрат. Квадрат вводять як рівносторонній прямокутник. Учитель пропонує серед даних на малюнку прямокутників або серед даних моделей знайти такі, в яких сторони рівні (мал. 165). Після цього він подає означення квадрата.
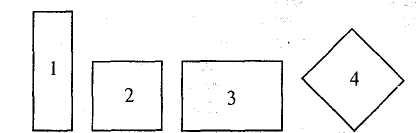
Мал. 165
298
Розділ XIV. Пропедевтика геометрії в початкових класах
Із введенням понять прямокутника і квадрата збагачуються вправи на розпізнавання многокутників. Адже тепер квадрат має чотири назви: квадрат, прямокутник, чотирикутник і многокутник, а прямокутник — три назви: прямокутник, чотирикутник і многокутник.
Наприкінці навчання в 2 класі запроваджуються вправи на розпізнавання многокутників у конфігураціях фігур.
Коло і круг. При введенні поняття кола і круга можна йти двома шляхами: а) розглянути спочатку коло як особливий вид кривої лінії, а потім ввести поняття круга як фігури, яку обмежує коло; б) розглянути круг, виходячи з відомого дітям поняття "кружечок", а коло ввести як лінію, яка обмежує круг. У зв'язку з тим, що кружечки, вирізані з паперу, потрібні для проведення предметної лічби вже з перших уроків математики, перевагу варто надати другому шляху.
Учитель повідомляє дітям, що на малюнку зображено круг (мал. 166).

Мал. 166
Лінія, яка є межею круга, називається колом. Коло будують за допомогою циркуля. Точка О, в якій міститься голка циркуля,— центр кола. Відрізок ОА — радіус кола.
З метою уточнення уявлень про коло і круг доцільно розглянути вправи виду:
.С
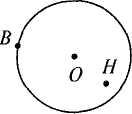
Мал. 167
Назвіть точки, які: а) належать кругу; б) належать колу; в) не належать у; г) належать кругу, але не належать колу (мал. 167).
Навчаючи дітей креслити коло за допомогою циркуля, вчитель спочатку демонструє таку побудову на аркуші білого паперу, прикріпленому до дошки. При цьому він ознайомлює їх з інструкцією побудови кола за допомогою циркуля:
1. Розвести ніжку циркуля і вістря олівця на величину заданого радіуса. Для цього голку треба встановити на нульову поділку лінійки, а вістря олівця — на поділку, числове значення якої дорівнює заданій величині радіуса.
2. Встановити голку в задану точку. Для цього правою рукою потрібно тримати олівець, а пальцем лівої руки спрямовувати вістря голки в задану точку.
3. Коло креслять в напрямі за годинниковою стрілкою, нахиливши циркуль трохи вперед у напрямі руху олівця. Починати креслити слід від нижньої точки кола (від себе).
Методика викладання математики в початкових-класах
299
4. Креслити коло треба однією правою рукою, тримаючи олівець за верхній кінець.
5. Лікоть правої руки спочатку відведений від корпуса, а відповідно до наближення вістря олівця до кінця (і початку) кола поступово наближається до нього.
Спочатку учні вчаться будувати коло на окремих аркушах паперу (на чернетках). Коли вони більш-менш правильно навчаться креслити коло, можна дозволити побудову кола в зошиті.
Є сенс і в тому, щоб ввести у 2 класі поняття діаметра кола. Вчитель пропонує дітям провести відрізок, який би проходив через центр кола і сполучав дві точки кола. Потім він повідомляє, що такий відрізок називається діаметром кола. Діаметр кола складається з двох радіусів.
Він поділяє круг на дві рівні частини.
Периметр многокутника. Означення периметра многокутника вводять у 2 класі. Як і довжину ламаної лінії, периметри многокутників знаходять у результаті вимірювання довжин їх сторін з подальшим додаванням здобутих результатів.
У 3 класі вводять буквене позначення многокутників. Це дає змогу урізноманітнити постановку завдань з геометричним змістом. Наприклад, серед даних фігур назвати прямокутники, квадрати тощо.
Пропонуються різні вправи на побудову многокутників на папері в клітинку. Причому такі завдання ускладнюють поділом фігури на задані многокутники.
Учні продовжують виконувати вправи на знаходження периметра многокутника. При цьому їм потрібно показати різні способи обчислення. Якщо довжину прямокутника позначити буквою а, а ширину — буквою Ь, то ці способи можна записати так: а + Ь + а + Ь; а + а + Ь + Ь; а • 2 + Ь • 2; (а + Ь) • 2. Останній спосіб найзручніший, але учні повинні бути ознайомлені з усіма способами.
У 4 класі діти продовжують виконувати вправи на розпізнавання і побудову плоских фігур, розв'язують інші задачі з геометричним змістом.
Геометричні задачі, пов'язані з периметром, дещо ускладнюються, більшість з них пов'язана з поняттям площі фігури.
Спостереження геометричних тіл і введення їх назв. Перші уявлення про геометричні тіла діти отримують у дошкільному віці. У початкових класах для розвитку цих уявлень можна використати уроки математики, малювання, а також моделювання з пластиліну на уроках праці, прогулянки та екскурсії.
Можливі такі види роботи з геометричними тілами: розгляд предметів, моделей, малюнків, що мають певну геометричну форму; поступове введення назв геометричних тіл; знаходження в навколишньому середовищі предметів відповідної назви (форми); моделювання геометричного тіла з пластиліну; виділення деяких елементів тіла (вершини, ребра, грані, основи); малювання на папері за зразком і вказівками вчителя.
У початкових класах варто дати школярам також поняття про такі геометричні тіла: кулю, куб, циліндр, прямокутний паралелепіпед, конус та піраміду. РОЗДШХУ
ПОЗАКЛАСНА РОБОТА З МАТЕМАТИКИ
Позакласна робота має бути невід'ємною частиною навчального виховного процесу. її головне завдання — виховувати інтерес до математики, стимулювати учнів до вивчення математики. У початковій школі доцільні насамперед ті види позакласної роботи, в яких можуть брати участь всі учні класу.
З молодшими школярами практикуються такі види позакласної роботи: позакласні години з математики, конкурси на кращого математика, математичні екскурсії, математичні ранки, математичні олімпіади, математичні гуртки. За формою і змістом вони вміщують коротенькі бесіди (повідомлення), цікаві вправи на обчислення, парні та групові змагання, математичні ігри, розв'язування головоломок і задач, розпізнавання геометричних фігур та ін.
