3.5.2 Линейная дельта-модуляция

В наиболее простом дельта-модуляторе используются шаги постоянного размера для всех уровней сигнала, поэтому он назы­вается равномерным, или линейным дельта-модулятором. Расчет линейного дельта-модулятора в основном связан с выбором размера постоянного шага и частоты дискретизации и направлен на удовлет­ворение двух критериев. Во-первых, отношение сигнал-гранулярный шум должно иметь определенное минимальное значение при наиболее низком уровне кодируемого сигнала. Во-вторых, отношение сигнал-шум перегрузки по крутизне должно иметь некое минималь­ное значение для самого высокого уровня сигнала, подлежащего кодированию.

Для удовлетворения критерия, связанного с перегрузкой по крутизне, удобно использовать выражение (3.12) и рассчитывать систему таким образом, чтобы перегрузка по крутизне наступала как раз на границе самого высокого уровня входного сигнала. Вследствие этого размер шага для самого большого уровня сигнала не является оптимальным в смысле качества восприятия или даже в смысле минимизации суммы гранулярного шума и шума перегруз­ки. Однако, когда имеется только гранулярный шум, характеристика ОСШК для дельта-модулятора может быть соответствующим образом сопоставлена с характеристикой ОСШК системы с ИКМ. Сопоставление этих двух методов кодирования при других условиях, например, тогда когда происходит перегрузка в любой из этих систем, требует оценки слушателями.

Уровень ожидаемой энергии от одиночной (без перегрузки) ошибки квантования в системе с дельта-модуляцией определяется из выражения (3.2) как q²/12 гдеq– размер шага. Однако вследст­вие относительно высокой частоты дискретизации в системе с ДМ спектр ошибок квантования занимает более широкую полосу, чем в системе с ИКМ. Благодаря этому выходной фильтр ДМ-декодера подавляет более высокий процент шума квантования, чем выходной фильтр ИКМ-декодера. Для частот дискретизации, которые более чем в 6 раз превышают максимальную частоту входного фильтра, шум квантования на выходе, по существу, пропорционален отноше­нию частоты среза фильтра к частоте дискретизации. Вследствие этого мощность шума квантования линейного дельта-модулятора может быть аппроксимирована следующим образом:

Мощность шума квантования линейной ДМ = (Kf_c/f_s)q², (3.13)

где f_c– частота среза выходного фильтра,f_s– частота дискретиза­ции, q – размер шага, К = 0,32.

Величина К в формуле (3.13) определялась многочисленными исследователями, получившими такие значения, как 0,18 [23]; 0,32 [24]; 0,51 [25] и 0,67 [26]. Нами выбрано значение 0,32, поскольку оно чаще всего используется и является исходным значе­нием, полученным де Ягером в его основополагающей работе в области дельта-модуляции [24]. Было предложено множество раз­новидностей дельта-модуляторов, что привело к появлению мно­жества других выражений для мощности шума квантования.

Если в качестве входного использовать синусоидальный сигнал с частотой f, то можно объединить выражения (3.12) и (3.13) и получить для отношения сигнал-шум квантования линейного дельта-модулятора следующее обычно используемое выражение:

ОСШК = (A²/2) / [(K f_c / f_s)(2fA/f_s)²], (3.14)

где в качестве входного сигнала принята синусоида Asin2ft, а размер шага выбран так, чтобы предотвратить перегрузку по крутизне [см. (3.12)].

При пользовании выражением (3.14) не следует забывать некото­рые важные предположения, принятые при его выводе. Во-первых, выражение (3.14) относится только к гранулярному шуму. Во-вторых, размеры шагов в этом выражении подогнаны к перегрузке по крутизне для конкретного синусоидального входного сигнала. Если размер шага согласно выражению (3.14) используется для входного сигнала с той же амплитудой, но с более высокой частотой, наступит перегрузка по крутизне. Кроме того, для сигналов с пони­женными уровнями получается меньшее ОСШК, если шаг имеет тот же размер. Наиболее обманчивый аспект формулы (3.14) состоит в том, что из нее следует, будто линейный дельта-модулятор дает более высокое значение ОСШК для низкочастотных сигналов, чем для высокочастотных. Это предположение справедливо, если размер шага подстроен под меньшую величину низкочастотного сигнала.

Зависимость (3.14) отображена на рис. 3.32 для различных частот входного сигнала. Отметим, что ОСШК улучшается на 9 дБ на октаву (удвоение) частоты дискретизации. В отличие от этого в системе с ИКМ ОСШК улучшается на 6 дБ с каждым добавочным разрядом. Вследствие этого системы с ИКМ дают лучшее качество при высоких скоростях передачи, а дельта-модуляторы – при низких скоростях передачи около 40 кбит/с.

При использовании синусоидального колебания с частотой 800 Гц в качестве испытательного сигнала из выражения (3.14) определяем (это же показывает и рис. 3.32), что для получения ОСШК, равного 26 дБ при линейной дельта-модуляции требуется частота дискретизации порядка 28 кГц. Соответствующую скорость передачи порядка 28 кбит/с следует сопоставить с четырьмя разрядами на дискрет, или со скоростью передачи 32 кбит/с линейной системы с ИКМ, для которой ранее было вычислено то же самое ОСШК.

Выражение (3.14) определяет ОСШК для синусоидального сигнала с постоянной амплитудой. Следующее соотношение опреде­ляет частоту дискретизации (скорость передачи), необходимую для получения конкретного ОСШК, и содержит также коэффициент динамического диапазона R:

fs= (25Rf²f_с*ОСШК)^1/3, (3.15)

где R—динамический диапазон (Amax/Аmin)²,f– частота вход­ного сигнала,f_c– частота среза выходного фильтра, ОСШК — требуемое минимальное значение отношения сигнал-шум квантова­ния.

Выражение (3.15) справедливо при предложении, что размер шага выбран исходя из отсутствия перегрузки по крутизне для сигнала с наивысшим уровнем:

q = 2A_max(f/f_s). (3.16)

Отметим снова, что выражения (3.15) и (3.16) соответствуют расчету дельта-модулятора с большим запасом, поскольку они не допускают перегрузки по крутизне. Однако они полезны, так как согласуются с расчетом ИКМ без перегрузки, представленным ранее.

Пример 3.5.Используя синусоидальное колебание с частотой 800 Гц в качестве входного сигнала, определите размер шага и частоту дискретизации в линейном дельта-модуляторе, необходимые для получения при кодировании речи ОСШК, равного 398 (26 дБ), и динамического диапазона порядка 1000 (30 дБ). Предполо­жим, что частота среза выходного фильтра равна 3,4 кГц.

Решение.Формулы (3.15) и (3.16) дают соответственно следующие значения для частоты дискретизации и размера шага:

q= 2А_max*800/279000 = 0,018 А_max= 0,56 А_max.

Скорость передачи 279 кбит/с следует сопоставить с 9 разрядами на дискрет и скоростью передачи 72 кбит/с, полученной ранее для ИКМ с равномерным шагом.

Размер шага, полученный в примере 3.5, достаточен лишь для того, чтобы только-только предотвратить перегрузку при максималь­ном уровне входного сигнала с частотой 800 Гц. Вследствие этого сигнал с более высокой частотой и той же амплитудой вызовет перегрузку кодера. Оценка усредненного спектра речи на рис. 3.24 показывает, однако, что частота 800 Гц находится вблизи частот составляющих с максимальной амплитудой, а на более высоких частотах в среднем мощность, значительно меньше. Вследствие этого единственный размер шага приблизительно подходит для передачи всего диапазона частот без перегрузки по крутизне. И действительно, на рис. 3.24 показано, что амплитуда составляющей с частотой порядка 2400 Гц обычно снижается примерно в 5,6 раза (на 15 дБ), в то время как требуется снизить ее только в 3 раза, чтобы получить крутизну меньше крутизны сигнала с частотой 800 Гц. Отсюда входной сигнал с частотой 800 Гц с достаточной точностью определяет размер шага, необходимый для исключения перегрузки по крутизне.

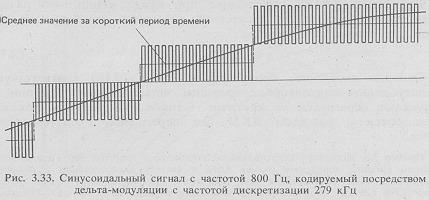
Довольно неожиданным результатом, полученным в примере 3.5, является относительно грубый шаг (0,56 A_min) используемый для кодирования синусоидального сигнала с минимальной амплиту­дой. Несмотря на это, дельта-модулятор дает ОСШК, равное 26 дБ, вследствие удаления входным фильтром большой части шумов квантования. На рис. 3.33 изображена часть грубо закодированной синусоиды с частотой 800 Гц при использовании частоты дискретизации и размера шага, полученных в примере 3.5. Показано также среднее за короткий период времени значение кодированного сигнала, которое для всех практических целей является эквивалент­ным входным сигналом для выходного фильтра. Отметим что высокая частота дискретизации дает очень тонкое разрешение для момента времени, когда сигнал пересекает границу квантования. Таким образом, дельта-модулятор кодирует сигнал с грубым кван­тованием по амплитуде, но с тонким квантованием по времени. В противоположность этому в системе с ИКМ используется относительно тонкое разрешение по амплитуде, но грубое квантова­ние по времени.

Основной недостаток линейной дельта-модуляции, подобно ИКМ с равномерным шагом, состоит в том, что сигналы и с низким и высоким уровнями кодируются шагом одного и того же размера. Вследствие этого сигналы с высоким уровнем кодируются с избы­точным качеством, что приводит к повышению скорости передачи. Решение, естественно, состоит в том, чтобы изменять размер шага в какой-то зависимости от крутизны входного сигнала. Обычно размер шага подстраивается постепенно в соответствии с усреднен­ным за короткое время значением крутизны сигнала.

При реализации дельта-модулятора большое значение имеет поддержание в кодере и декодере равенства шагов в положительную и отрицательную сторону. Если размеры шагов различаются в декодере, то в восстановленном сигнале накапливается смещение за счет постоянной составляющей, что может привести к насыщению цепей. Как будет показано в следующем разделе, с небольшим различием размеров шагов в декодере можно сравнительно легко примириться. В то же время различие размеров шагов в кодере доставляет больше неприятностей и требует пристального внимания.

Когда в дельта-модуляторе кодируется сигнал незагруженного канала (пауза речи), выходной цифровой сигнал с идеальной точностью меняется между 0 и 1. Если происходит именно такое изменение, выходной фильтр декодера устраняет относительно высокочастотные шумы дискретизации. Однако, если размеры шагов различаются, как показано на рис. 3.34, то случайно могут появиться две последовательные единицы или два последовательных нуля. Поскольку пары нулей или единиц появляются относительно редко, они создают низкочастотные искажения, которые не отфильтровы­ваются и проявляются в виде шумов незагруженного канала. Шумы незагруженного канала представляют особую проблему при разра­ботке дельта-модуляторов из-за относительно больших шагов кван­тования (см. пример 3.5). Одним из средств балансировки размеров шагов в кодере является вычитание смещения, получаемого низко­частотной фильтрацией (интегрированием) сигнала в цепи обратной связи в течение длительного периода времени [20].