
- •Устойчивость линеаризованных систем
- •Алгебраические критерии устойчивости
- •Критерий устойчивости Гурвица
- •Указанные главные определители называются определителями Гурвица и имеют вид:
- •Для системы четвертого порядка
- •Критерий устойчивости Михайлова
- •Определение критерия Михайлова
- •Определение границ устойчивости по критерию Михайлова.
Устойчивость линеаризованных систем
Устойчивость CАУ включает в себя требованиезатухания всех переходных процессов во времени. Системы с расходящимися процессами были бы неработоспособными.
Все реальные системы в технике и в природе, как правило, являются в большей или меньшей степени нелинейными. Однако многие системы можно считать близкими к линейным и с необходимой для практики точностью проектировать как линейные.
Рассмотрим сначала идеально линейную систему.
![]() ,
,
где g(t) – задающее воздействие.
Решение для регулируемой величины имеет вид:
![]() .
.
Первая часть решения хсоб(t) представляет переходной процесс в замкнутой системе управления.
![]() ,
,
где
i
– корни характеристического уравнения
D()=0,
все
различные,
а
постоянные
Сi
определяются
по начальным условиям, после добавления
частного решения
![]() .
.
Устойчивостью линейной системы – это свойство затухания переходного процесса с течением времени, или следующее свойство собственного (свободного) движения системы хсоб(t) 0 при t
Корни характеристического уравнения могут быть вещественные, комплексные, мнимые.
Вещественные корни.
Если
1= –а1,
тогда
![]() приt
получится
затухающий процесс (a).
приt
получится
затухающий процесс (a).
Если
2= +а2,
тогда
![]() приt
получится
расходящийся процесс (б).
приt
получится
расходящийся процесс (б).
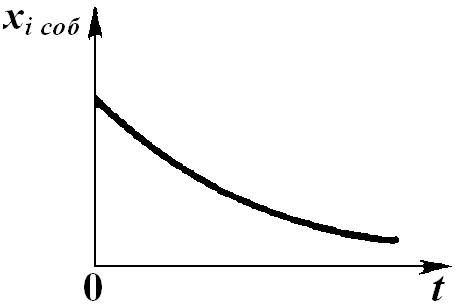
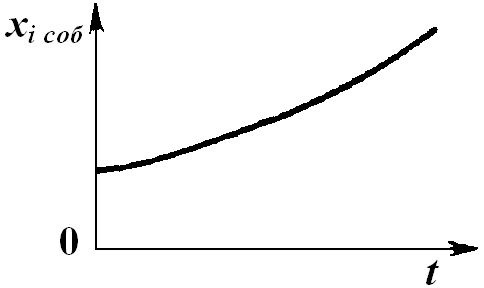
a) б)
2) Комплексные корни (они попарно сопряжены).
Если
1, 2= –1 j,
тогда
![]() и
при
t
получится
затухающий процесс (1
–
параметр
затухания, определяет
затухание огибающей) (a).
и
при
t
получится
затухающий процесс (1
–
параметр
затухания, определяет
затухание огибающей) (a).
Если
1, 2= 1 j,
тогда
![]() и
при
t
получится
расходящийся процесс (б).
и
при
t
получится
расходящийся процесс (б).


б)
3) Чисто мнимые корни
Если
1, 2= j,
тогда
![]() и
получим
незатухающие колебания с постоянной
амплитудой.
и
получим
незатухающие колебания с постоянной
амплитудой.
Для затухания переходных процессов необходимо и достаточно, чтобы все корни характеристического уравнения i = (i, 1, 2, …, n) обладали отрицательными вещественными частями.
Если в характеристическом уравнении системы имеется хотя бы один нулевой корень i = 0 или хотя бы одна пара чисто мнимых корней i, i+1 = j, а все остальные корни имеют отрицательные вещественные части, то система находится на границе устойчивости.
Если в характеристическом уравнении системы имеется хотя бы один корень с положительной вещественной частью, а все остальные корни имеют отрицательные вещественные части, то система будет неустойчивой.
Это следует из того, что нулевой корень можно рассматривать как границу между отрицательным и положительным, а чисто мнимый корень – как границу между комплексными корнями с отрицательной и положительной вещественными частями.
Теорема: Для того чтобы линейная система была устойчивой необходимо и достаточно, чтобы все корни характеристического уравнения располагались в левой полуплоскости комплексного переменного .

Мнимая ось плоскости корней служит границей устойчивости.
Можно выделить два типа границ устойчивости линейной системы,:
1) апериодическая, характеризуется нулевым корнем 1 = 0;
2) колебательная, характеризуется парой чисто мнимых корней 12 = j; при этом имеем решение хсоб(t) =Asin(t+), где A и определяются начальными условиями, а значение мнимой части корня равно частоте незатухающих колебаний системы на границе устойчивости.
