[TAK] / Leczii / Lek2_mul_E

Уравнения звеньев и виды основных характеристик

Проектирование системы автоматического управления всегда начинается с разработки математической модели системы, т.е. составления динамических уравнений, описывающих физические процессы, протекающие в системе. Вся система разбивается на отдельные звенья и для каждого звена составляется свое уравнение.

З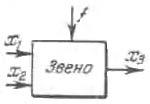 вено может иметь не одну входную величину, а несколько. Кроме входной и выходной величин звена, которые выражают собой внутренние связи между звеньями данной системы, может учитываться также внешнее воздействие.

Звено системы – это техническое устройство любой физической природы, конструкции и назначения, которое описывается определенным дифференциальным уравнением.

В общем случае уравнение динамики звена системы является нелинейным

Мы будем рассматривать только звенья, динамика которых описывается линейными уравнениями. В общем случае это уравнение имеет вид:

где x₁ – входная, а x₂ – выходная переменная.

Введем оператор , который обозначает операцию дифференцирования.

Получим уравнение звена в символической форме

Передаточная функция звена

Дифференциальное уравнение можно также записать в другом виде:

или

.

Выражение W(p) называется передаточной функцией звена, а коэффициент k = b_m / a_n - общим коэффициентом усиления (передачи)звена.

В ТАУ принято записывать уравнения звена таким образом, чтобы выходная величина входили в уравнение с коэффициентом 1

.

Передаточная функция звена – это отношение изображений Лапласа выходной и входной величин при нулевых начальных условиях.

при н.у.=0.

В выражении преобразование Лапласа функции z(t) определяется следующим образом:

,

где s – комплексная переменная, символ  обозначает операцию преобразования Лапласа функции, стоящей в квадратных скобках.

Основные свойства преобразования Лапласа

1. Линейность:

,

;

2. Преобразование производной:

( при нулевых начальных условиях);

3. Преобразование интеграла:

4. Запаздывание:

.

Пример. Рассмотрим следующее уравнение

.

Пусть даны нулевые начальные условия

                     .

Запишем преобразования Лапласа для входной и выходной величин

.

Тогда

        .

Получим

.

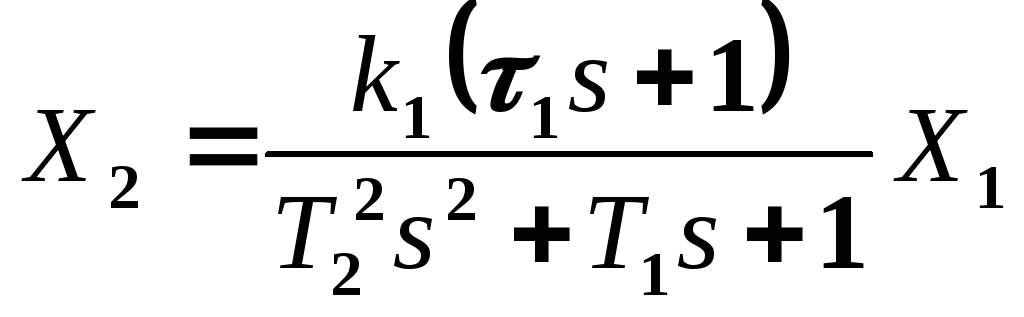
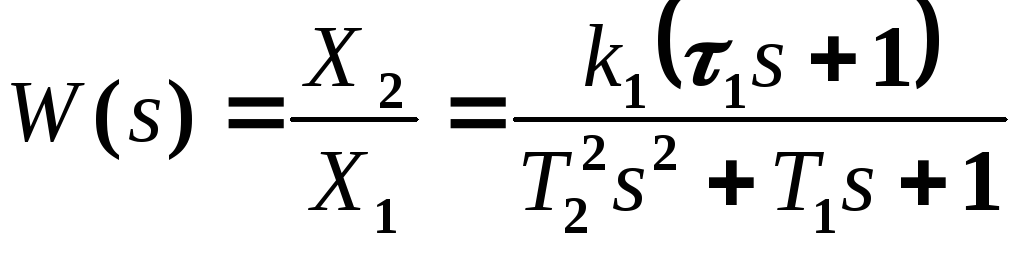где k₁ – общий коэффициент усиления (передачи), Т₁, Т₂, ₁ – постоянные времени.

В общем случае передаточная функция звена определяется выражением

,

где N(s) и L(s) – многочлены с коэффициентами 1 в младших членах, причем степень N(s), как правило, ниже степени L(s).

Дифференциальное уравнение звена

Зная передаточную функцию звена можно записать дифференциальное уравнение этого звена.

Пусть , тогда в общем виде уравнение можно записать , где оператор обозначает операцию дифференцирования.

Если знаменатель передаточной функции приравнять 0, то получим характеристическое уравнение L(λ)=0 .

Корни характеристического уравнения называются полюсами передаточной функции.

Если числитель передаточной функции приравнять 0 (N(λ)=0) и решить это уравнение, то корни данного уравнения называются нулями передаточной функции.

Пример.

Передаточная функция звена .

Характеристическое уравнение . Полюса – это корни данного уравнения.

Нули передаточной функции – это корни уравнения.

Основные виды динамических характеристик звена

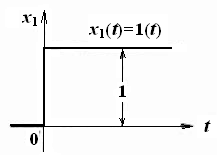
Переходная функция звена

Переходной функцией звена h(t) называется реакция звена на единичное ступенчатое воздействие, т.е. переходной процесс на выходе х₂(t) при скачке 1(t) на входе х₁(t)

х₂(t) = h(t)

Импульсная переходная функция звена

(Весовая функция звена)

Импульсной переходной (весовой) функцией звена (t) называется реакция звена на единичную импульсную функцию, так называемую дельта-функцию.

Дельта-функция представляет собой производную от единичной ступенчатой функции и равна нулю повсюду, кроме точки t = 0, где она равна .

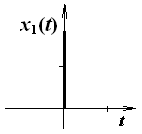
Связь между переходной функцией и импульсной переходной функцией:

Переходная фунция:

х₁(t) = 1(t), то х₂(t) = h(t) ,

Импульсная переходная функция:

, то

Отсюда следующее соотношение между весовой и переходной функциями звена

, .

Частотные характеристики звена

Частотными характеристиками звена называются формулы и графики, характеризующие реакцию звена на синусоидальное входное воздействие в установившемся режиме, т.е. вынужденные синусоидальные колебания звена.

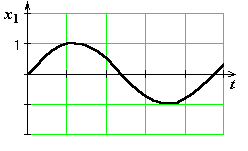
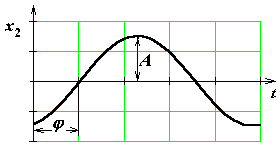
Е сли на вход звена подается х₁(t) = sint, то на выходе звена будет (в установившемся режиме) сигнал х₂(t) = Asin(t+), где A – амплитуда (усиление амплитуды),   – фаза (сдвиг по фазе)

В ТАУ для нахождения выражения для частотной характеристики применяют комплексное синусоидальное входное воздействие вида

х₁(t)=е^jt, или х₁(t)=cos(t)+jsin(t).

Пусть имеется уравнение

.

Если х₁(t)= е ^jt, , тогда

, , .

Подставив эти величины в уравнение звена, получим

,

откуда

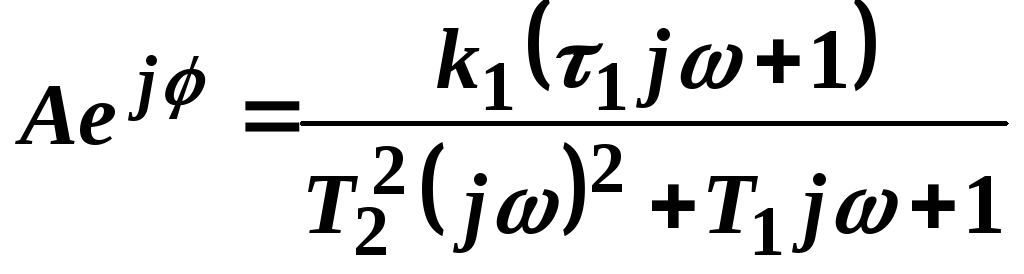
Сравнивая это выражение с передаточной функцией данного звена, видим, что

W(j) – амплитудно-фазовая частотная характеристика звена (АФЧХ)

– амплитудная частотная характеристика (АЧХ) .

– фазовая частотная характеристика (ФЧХ).

Графически амплитудно-фазовая частотная характеристика (АФЧХ) строится на комплексной плоскости в полярных координатах (A, ), как годограф функции W(j). Можно с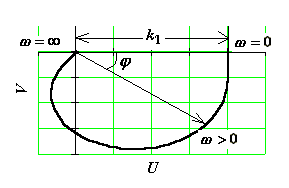 троить АФЧХ и в прямоугольных координатах (U, V ), выделив в выражении W(j) вещественную и мнимую части:

Амплитудно-фазовая частотная характеристика (АФЧХ) – это геометрическое место концов векторов амплитуд на комплексной плоскости, которые соответствуют передаточной функции W(j)=U()+jV() при изменении круговой частоты от нуля до бесконечности.

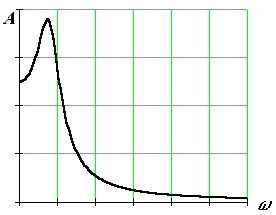
Амплитудная частотная характеристика (АЧХ) показывает изменение амплитуды выходно­го сигнала относительно амплитуды входного сигнала при изменении частоты от нуля до бесконечности.

Амплитудная частотная характеристика показывает, как пропускает звено сигнал различной частоты. Оценка пропускания делается по отношению выходной и входной величин.

Фазовая частотная характеристика (ФЧХ) показывает сдвиг фазы выходного сигнала относительно фазы входного сигнала при изменении частоты от нуля до бесконечности.

Фазовая частотная характеристика показывает фазовые сдвиги, вносимые звеном на различных частотах.

А ЧХ – четная функция, ФЧХ – нечетная функция.

Логарифмические частотные характеристики

При построении логарифмической АЧХ по оси ординат откладывается величина:

,

которая измеряется в децибелах.

По оси абсцисс откладывается круговая частота в логарифмическом масштабе.

Начало координат обычно помещают в точку  = 1, т.к. lg1 = 0 (точка  = 0 лежит в – ). Ось абсцисс (Lm = 0) соответствует значению А = 1. При этом верхняя полуплоскость ЛАХ соответствует значениям А > 1 (усиление амплитуды), нижняя полуплоскость – значениям А < 1 (ослабление амплитуды).

Точка пересечения ЛАХ с осью абсцисс называется частотой среза. При этой частоте амплитуды входного и выходного сигналов равны.

П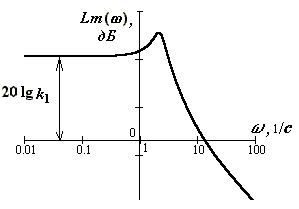 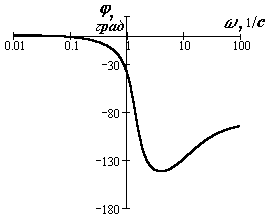ри построении логарифмической ФЧХ отсчет углов по оси ординат идет в обычном масш­табе в угловых градусах. По оси абсцисс откладывается частота в логарифмическом масштабе