35

Індивідуальні завдання Варіант №1

1. Розв’язати рівняння= 0

2.Обчислити визначник двома способами: а) отримавши нулі у якому-небудь рядку; б) привести визначник до трикутного виду.

3.Обчислити:+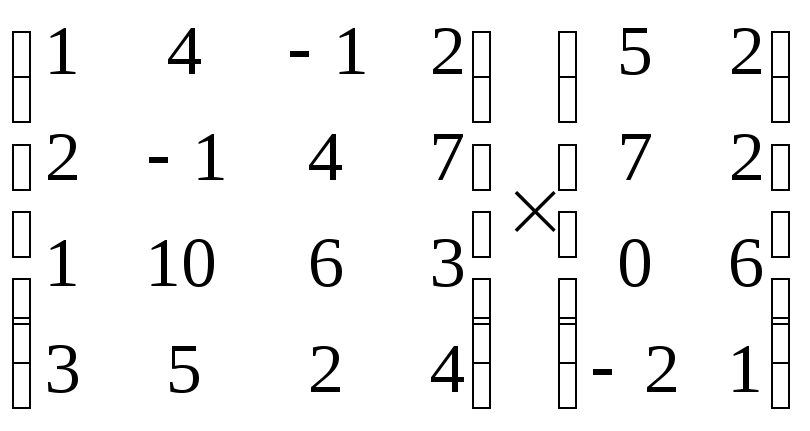

4. Дани матриці. Вказати всі випадки для яких можливий добуток двох матриць, а також записати розміри відповідних добутків:.

5. Найдіть обернену матрицюдля матрицідвома способами:

а) за формулою; б) за допомогою одиничної матриці.

6.Визначити ранг матриці:

7.Довести сумісність СЛАР та розв’язати: а) за формулами Крамера; б) методом Гауса; в) використовуючи зворотну матрицю.

8.Розв’язати однорідну СЛАР:

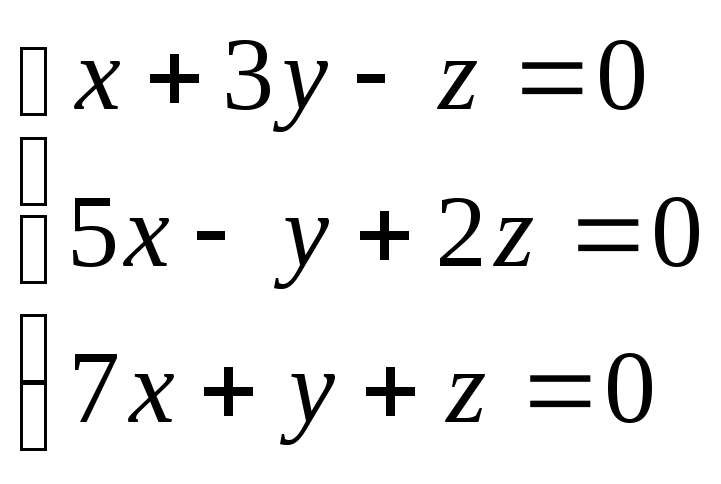
9.Побудувати фундаментальну систему розв’язків, для однорідної системи:

Варіант №2

1.Розв’язати рівняння:

= 0

2.Обчислити визначник двома способами: а) отримавши нулі у якому-небудь рядку; б) привести визначник до трикутного виду.

3.Обчислити:

+

4.Дани матриці. Вказати всі випадки для яких можливий добуток двох матриць, а також записати розміри відповідних добутків:.

5.Найдіть обернену матрицюдля матрицідвома способами:

а) за формулою; б) за допомогою одиничної матриці

6.Визначити ранг матриці:

7.Довести сумісність СЛАР та розв’язати: а) за формулами Крамера;

б) методом Гауса; в) використовуючи зворотну матрицю.

8.Розв’язати однорідну СЛАР:

9.Побудувати фундаментальну систему розв’язків, для однорідної системи:

Варіант №3

1. Розв’язати рівняння:

= 0

2.Обчислити визначник двома способами: а) добувши нулі у якому-небудь ряду; б) привівши визначник до трикутного виду.

3. Обчислити:

+

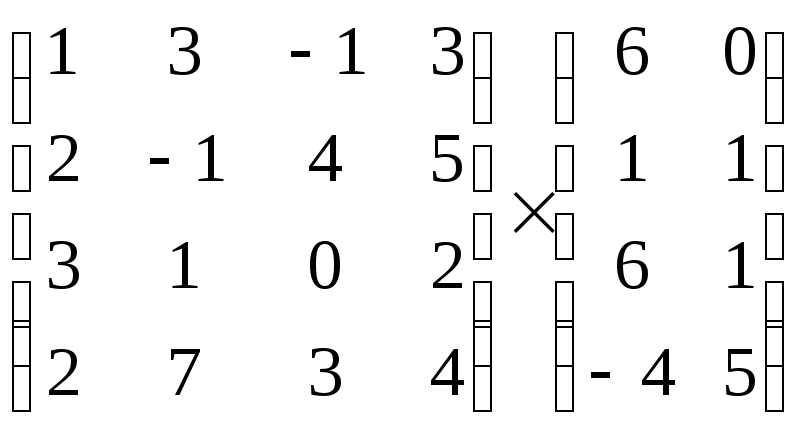4. Дани матриці. Вказати всі випадки для яких можливий добуток двох матриць, а також записати розміри відповідних добутків А(34), В(23), С(45), F(32).

5. Найдіть обернену матрицюдля матрицідвома способами: а) за формулою; б) за допомогою одиничної матриці.

6. Визначити ранг матриці:

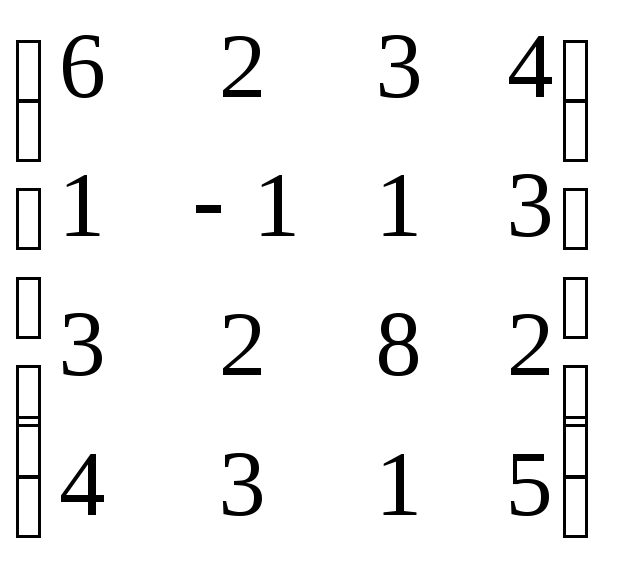
7.Довести сумісність СЛАР та розв’язати: а) за формулами Крамера;

б) методом Гауса; в) використовуючи зворотну матрицю

8.Розв’язати однорідну СЛАР:

9.Побудувати фундаментальну систему розв’язків, для однорідної системи:

Варіант №4

1.Розв’язати рівняння:

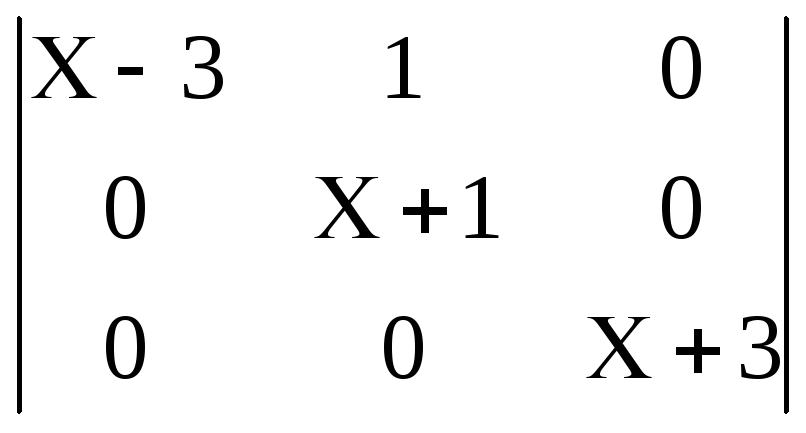= 0

2.Обчислити визначник двома способами: а) отримавши нулі у якому-небудь рядку; б) привести визначник до трикутного виду

3.Обчислити:

+

4.Дани матриці. Вказати всі випадки для яких можливий добуток двох матриць, а також записати розміри відповідних добутків:.

5.Найдіть обернену матрицюдля матриці А двома способами:

а) за формулою; б) за допомогою одиничної матриці:

6.Визначити ранг матриці:

7.Довести сумісність СЛАР та розв’язати: а) за формулами Крамера;

б) методом Гауса; в) використовуючи зворотну матрицю.

8.Розв’язати однорідну СЛАР:

9.Побудувати фундаментальну систему розв’язків, для однорідної системи:

Варіант №5

1.Розв’язати рівняння:

= 0

2.Обчислити визначник двома способами: а) отримавши нулі у якому-небудь рядку; б) привести визначник до трикутного виду.

3.Обчислити:

+

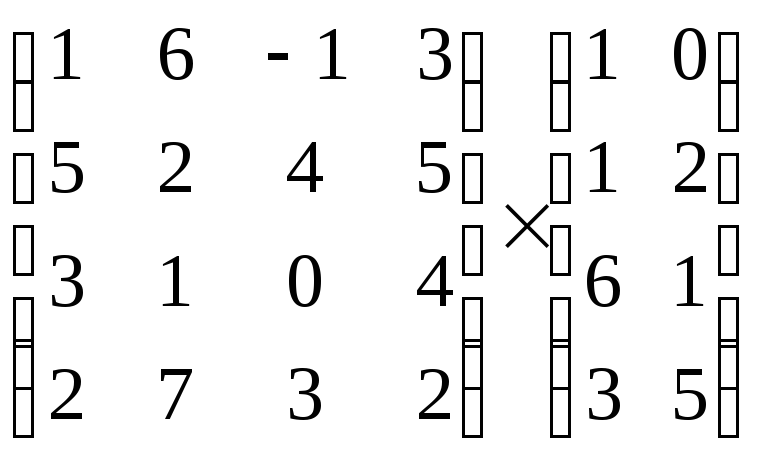4.Дани матриці. Вказати всі випадки для яких можливий добуток двох матриць, а також записати розміри відповідних добутків:.

5.Найдіть обернену матрицюдля матриці А двома способами:

а) за формулою; б) за допомогою одиничної матриці.

6.Визначити ранг матриці:

7.Довести сумісність СЛАР та розв’язати : а) за формулами Крамера;

б) методом Гауса; в) використовуючи зворотну матрицю.

8.Розв’язати однорідну СЛАР:

9. Побудувати фундаментальну систему розв’язків, для однорідної системи: