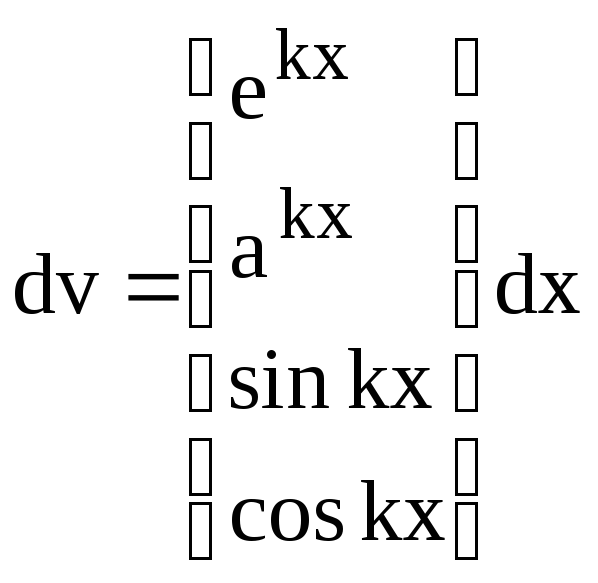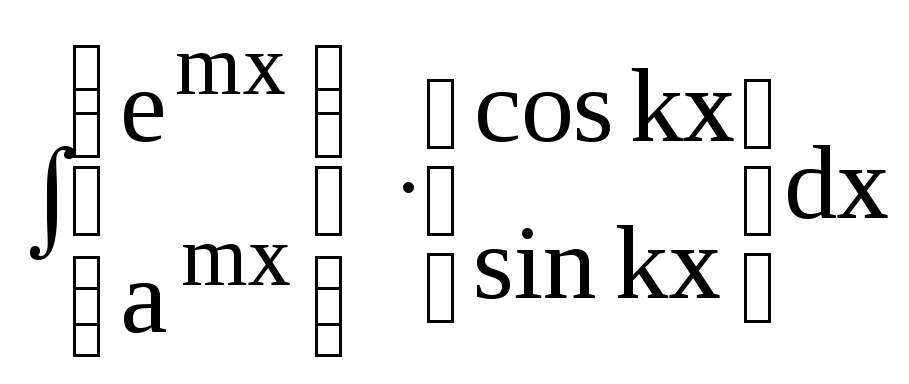- •Міністерство освіти і науки,
- •1.3.2 Метод підстановки (метод заміни змінної)
- •1.3.8 Деякі тригонометричні підстановки
- •1.4 Індивідуальні завдання
- •1.4.1 Знайти інтеграли безпосереднім інтегруванням
- •1.4.2 Знайти інтеграли за допомогою внесення сталої, змінної, функції під знак диференціалу або методом підстановки
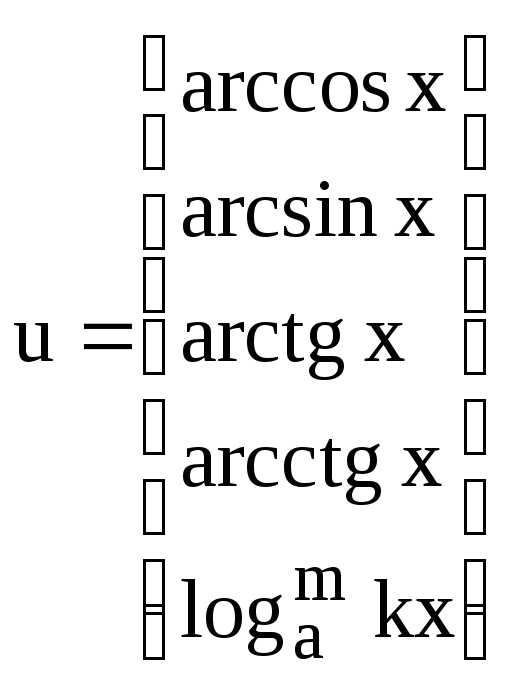
- •1.4.3 Знайти інтеграли методом інтегрування частинами
- •1.4.4 Знайти інтеграли від функцій, що містять квадратний тричлен у знаменнику
- •1.4.5 Знайти інтеграли від дробово-раціональних функцій
- •1.4.6 Знайти інтеграл від ірраціональної функції
- •1.4.7 Знайти інтеграли від тригонометричних функцій (приклад (в) на універсальну тригонометричну підстановку)
- •1.4.8 Знайти інтеграл, використавши відповідну тригонометричну підстановку
- •2. Визначений інтеграл
- •2.1 Аудиторні завдання
- •2.2 Індивідуальні завдання
- •2.2.1 Обчислити наступні інтеграли:
- •2.2.2 Обчислити невласні інтеграли або встановити їх розбіжність
- •2.2.3 Обчислити площі фігур, обмежених вказаними лініями
- •2.2.4 Обчислити довжину дуги кривої, заданої в прямокутних координатах
- •2.2.5 Обчислити довжину дуги кривої, заданої параметрично
- •2.2.6 Обчислити довжину дуги кривої, заданої в полярних координатах
- •2.2.7 Обчислити об’єм тіла обертання (вісь обертання ох)
- •2.2.8 Знайти координати центра мас однорідної кривої l
- •2.2.9 Знайти координати центра мас однорідної фігури ф, обмеженої вказаними лініями
- •Л і т е р а т у р а
Міністерство освіти і науки,
МОЛОДІ ТА СПОРТУ УКРАЇНИ
Запорізький національний технічний університет
ІНДИВІДУАЛЬНІ ЗАВДАННЯ
з вищої математики
для студентів
технічних спеціальностей
денної форми навчання
(2-й семестр)
1 частина
2011
Індивідуальні завдання з вищої математики для студентів технічних спеціальностей денної форми навчання (2-й семестр, 1частина) / Укл.: Скуйбіда Л. Г., Слюсарова Т. І. - Запоріжжя: ЗНТУ, 2011 - 70 с.


Укладачі:
Розділ «Невизначений інтеграл» - Т. І. Слюсарова, ас.
Розділ «Визначений інтеграл» - Л. Г. Скуйбіда, ст. викл.; Т. І. Слюсарова, ас.
Рецензент: І. М. Килимник, доц., к.т.н.
Відповідальний за випуск: Т. І. Слюсарова, ас.
Комп’ютерна верстка: С. І. Давиденко С. І., Т. І. Слюсарова
Затверджено на засіданні
кафедри вищої математики ЗНТУ
Протокол № 7 від 25.05.11
ЗМІСТ
|
1. Невизначений інтеграл |
4 |
|
1.1 Таблиця інтегралів |
4 |
|
1.2 Правила інтегрування |
5 |
|
1.3 Аудиторні завдання |
7 |
|
1.4 Індивідуальні завдання |
14 |
|
2. Визначений інтеграл |
42 |
|
2.1 Аудиторні завдання |
42 |
|
2.2 Індивідуальні завдання |
45 |
|
Література |
70 |
1. НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
1.1 Таблиця інтегралів:
![]() ;
;
1)
![]() ;
;
2)
![]() ;
;![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)![]() ;
;
10)![]() ;
;
11)![]() ;
;
12)![]() ;
;
13)
![]() ;
;![]() ;
;
14)
![]() ;
;
15)
![]() ;
;
16)
![]() ;
;
17)
![]() ;
;
18)
![]() ;
;
19)
![]()
20)
![]() ;
;
21)
![]() ;
;
22)
![]() ;
;
23)
![]() .
.
1.2 Правила інтегрування
1.
![]() де
де![]() k- стала величина
k- стала величина
2.
![]()
3.![]()
4. Інтегрування частинами:
![]() ,
або
,
або
![]()
5.
Заміна змінної :![]() ,
де
,
де![]()
Деякі підстановки
|
№ з/с |
вид інтегралу |
підстановка |
вираз
для
|
новий інтеграл |
|
1. |
|
|
|
|
|
2. |
|
|
|
|
|
3. |
|
|
|
|
|
4. |
|
|
|
|
|
5. |
|
|
|
|
|
6. |
|
|
|
|
|
7. |
|
|
|
|
|
8. |
|
|
|
|
|
9. |
|
|
|
|
|
10. |
|
|
|
|
|
11. |
|
|
|
|
|
12. |
|
|
|
|
Деякі види інтегралів,
для яких застосовується метод інтегрування частинами
|
№ з/с |
Вид інтегралу |
Що
брати за
|
Що
брати за
|
|
1. |
|
|
|
|
2. |
|
|
|
|
3. |
|
будь-який з множників |
будь-який з множників |
|
4. |
|
|
|
|
| |||
1.3 Аудиторні завдання
1.3.1 Безпосереднє інтегрування. Внесення сталої, змінної або функції під знак диференціалу
|
1. |
|
Відповідь: |
|
2. |
|
Відповідь:
|
|
3. |
|
Відповідь:
|
|
4. |
|
Відповідь:
3 |
|
5. |
|
Відповідь:
|
|
6. |
|
Відповідь:
|
|
7. |
|
Відповідь:
|
|
8. |
|
Відповідь:
|
|
9. |
|
Відповідь:
|
|
10. |
|
Відповідь:
|
|
11. |
|
Відповідь:
|
|
12. |
|
Відповідь:
|
|
13. |
|
Відповідь:
|
|
14. |
|
Відповідь:
|
|
15. |
|
Відповідь:
|