
Завдання для самостійного розвязування
З’ясуйте, які з наведених нижче відображень
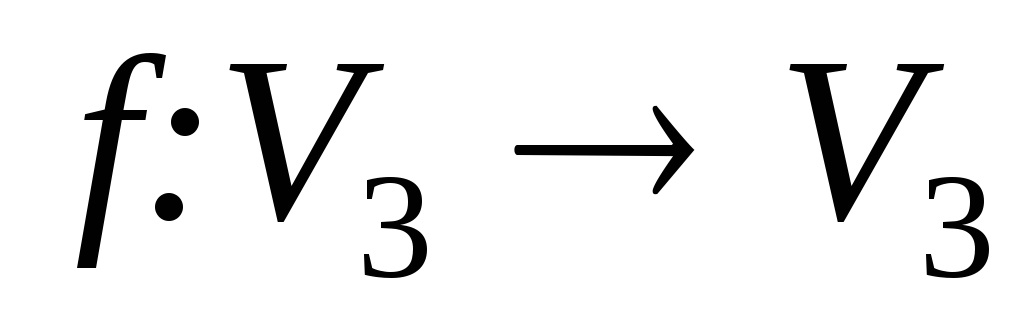 ,
де
,
де – простір вільних векторів, є лінійними
операторами. Знайдіть матриці лінійних
операторів в базисі
– простір вільних векторів, є лінійними
операторами. Знайдіть матриці лінійних
операторів в базисі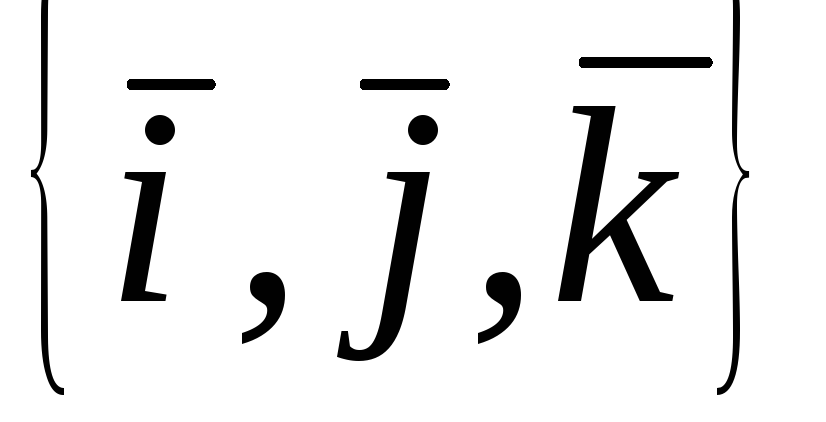 (
(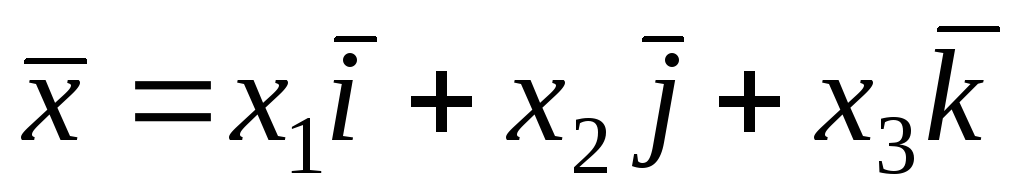 ):
):1)
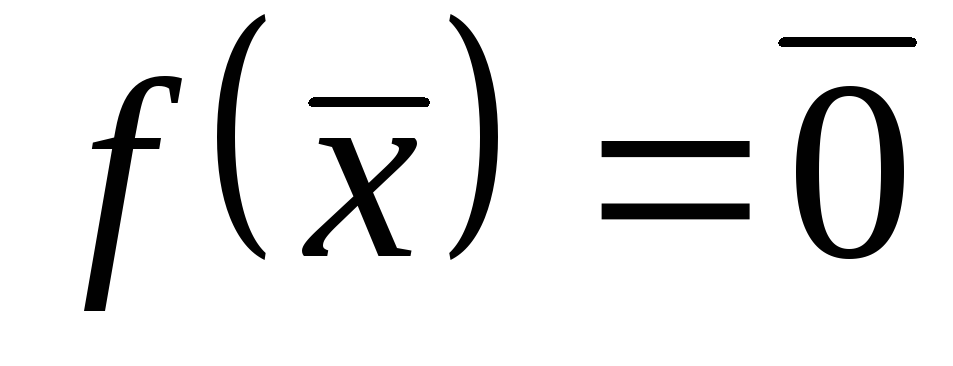 ;
;6)
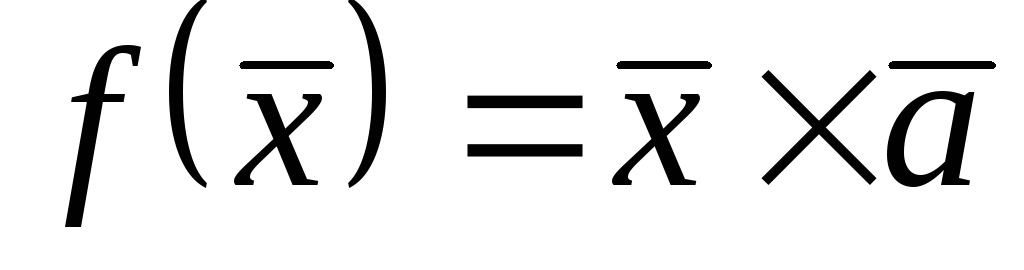 ,
де
,
де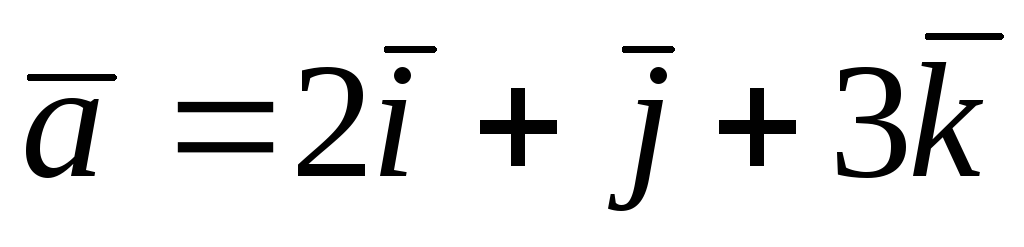 ;
;2)
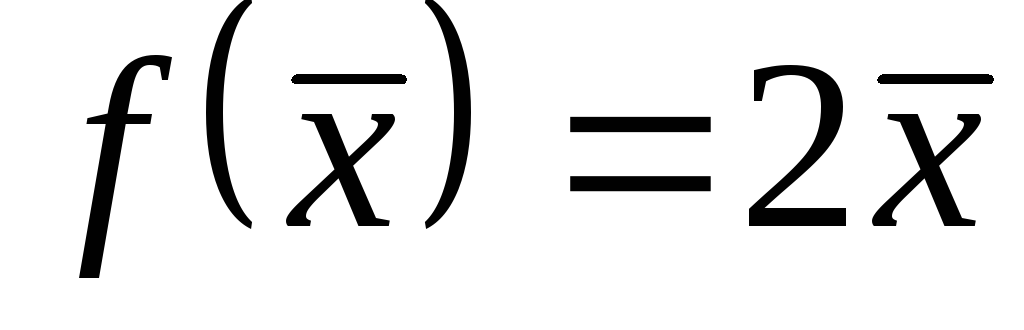 ;
;7)
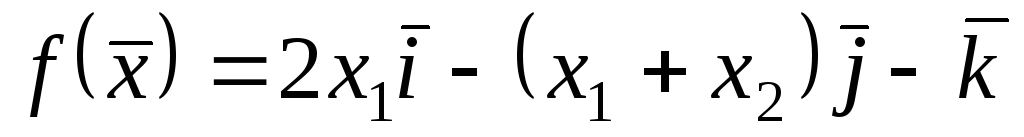 ;
;3)
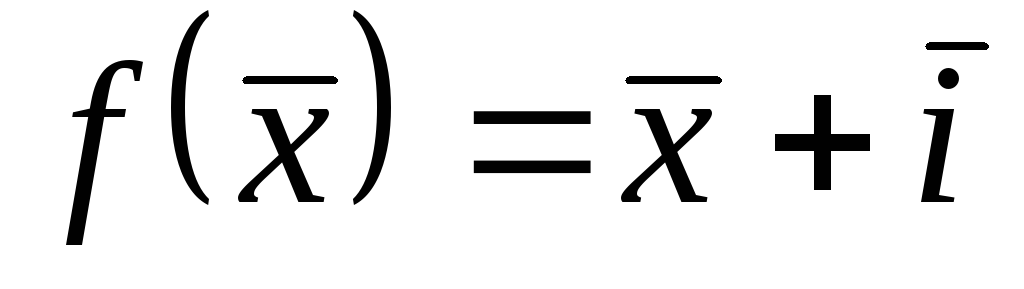 ;
;8)
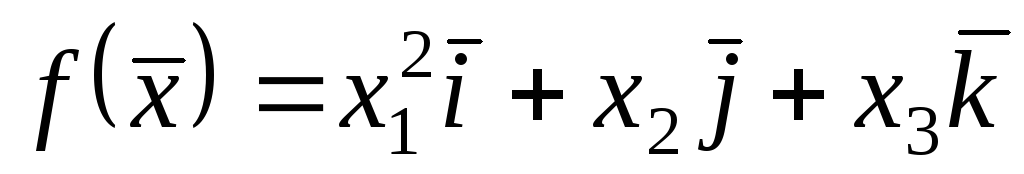 ;
;4)
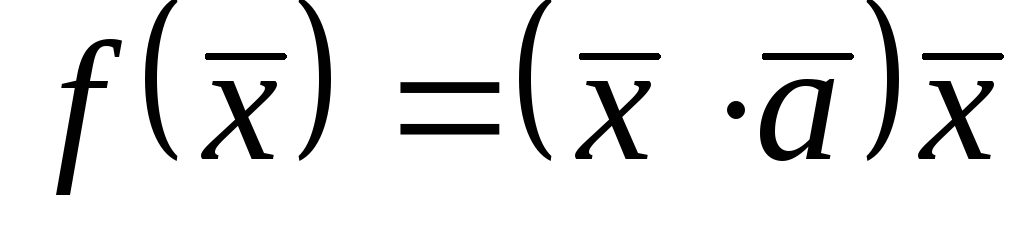 ,
де
,
де – деякий вектор;
– деякий вектор;9)
 ;
;5)
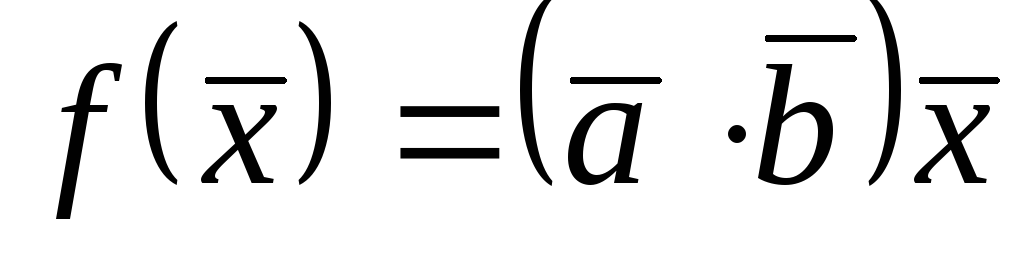 ,
де
,
де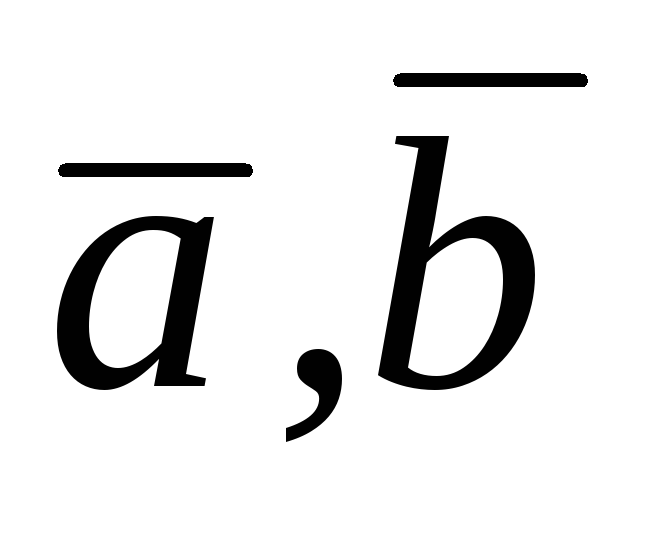 – деякі вектори;
– деякі вектори;10)
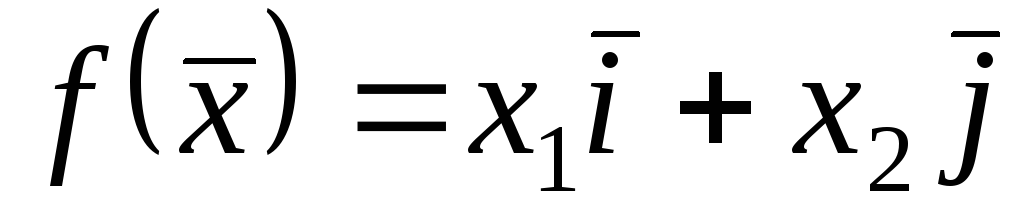 .
.Укажіть, які з наведених перетворень простору
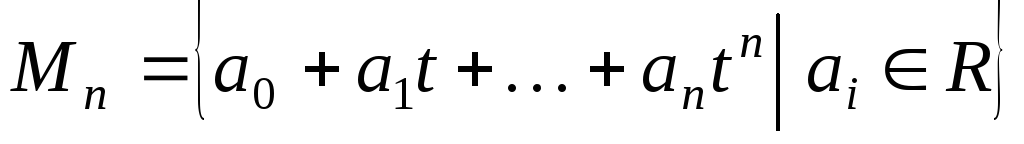 є лінійними операторами, знайдіть їх
матриці в базисі
є лінійними операторами, знайдіть їх
матриці в базисі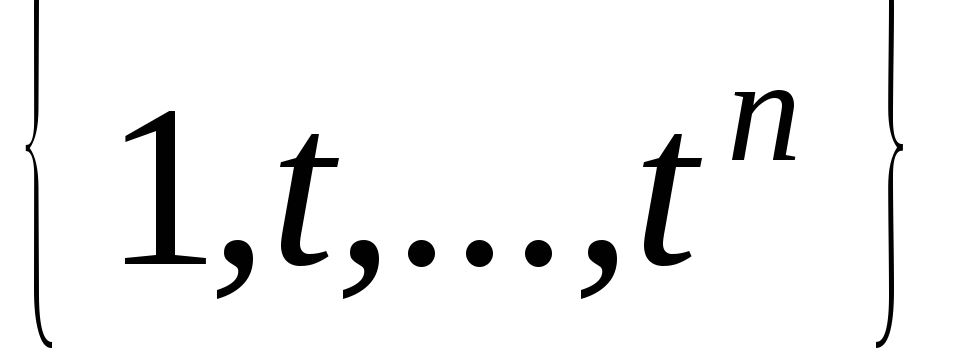 :
:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ,
де
,
де![]() – фіксовані числа,
– фіксовані числа,![]() ;
;
4)
![]() – оператор диференціювання.
– оператор диференціювання.
Перевірте, чи є оператори лінійними, якщо так, то знайдіть їх матриці в базисі
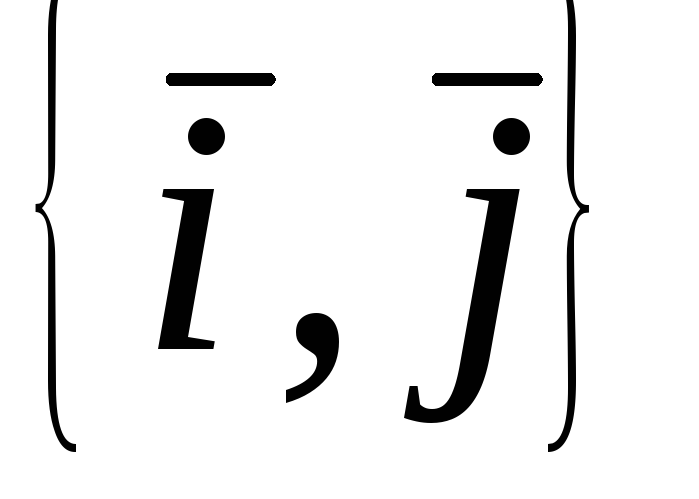 для
для та
та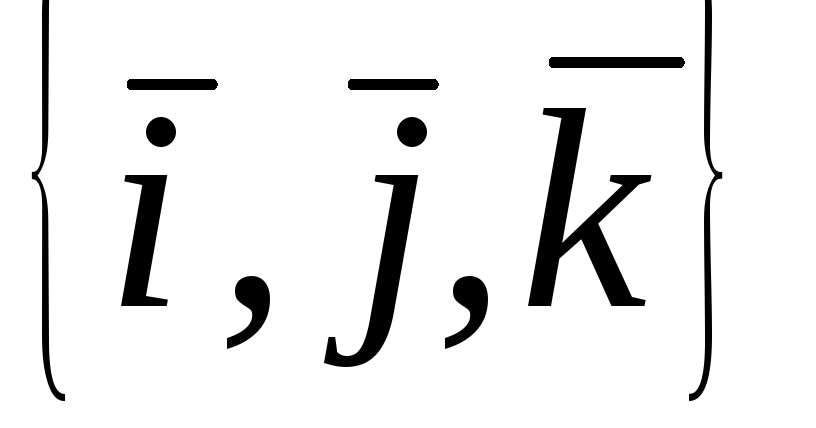 для
для :
:
1) оператор
![]() осьової симетрії відносно осі
осьової симетрії відносно осі![]() в площині
в площині![]() ,
якщо вісь
,
якщо вісь![]() нахилена до
нахилена до![]() під кутом
під кутом![]() ;
;
2) оператор
ортогонального проектування площини
![]() на дану пряму, що нахилена до
на дану пряму, що нахилена до![]() під кутом
під кутом![]() ;
;
3) оператор
![]() симетрії простору
симетрії простору![]() відносно площини
відносно площини![]() ,
що проходить через початок координат
ортогонально вектору
,
що проходить через початок координат
ортогонально вектору![]() ;
;
4) оператор
проектування простору
![]() на вісь вектора
на вісь вектора![]() паралельно координатній площині векторів
паралельно координатній площині векторів![]() .
.
З’ясуйте, які з перетворень
 тривимірного простору є лінійними
операторами, знайдіть матриці лінійних
операторів в тому ж базисі, в якому
задані координати векторів
тривимірного простору є лінійними
операторами, знайдіть матриці лінійних
операторів в тому ж базисі, в якому
задані координати векторів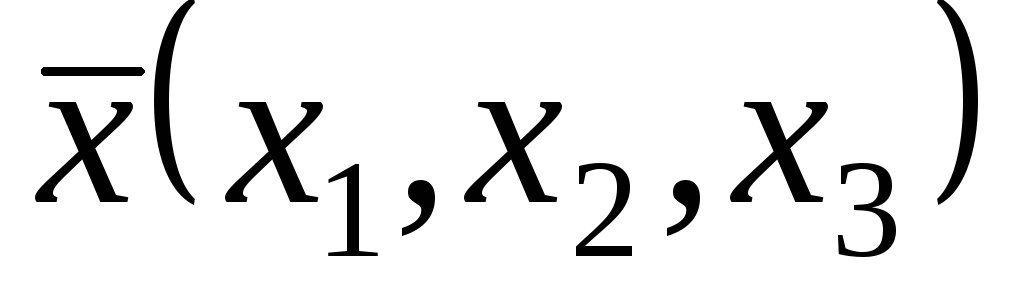 та
та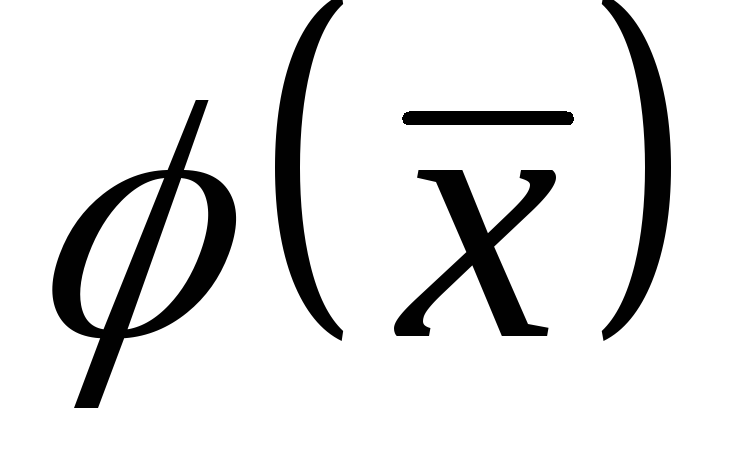 ,
якщо:
,
якщо:1)
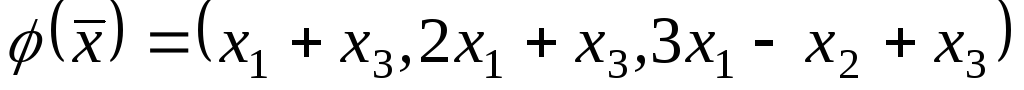 ;
;5)
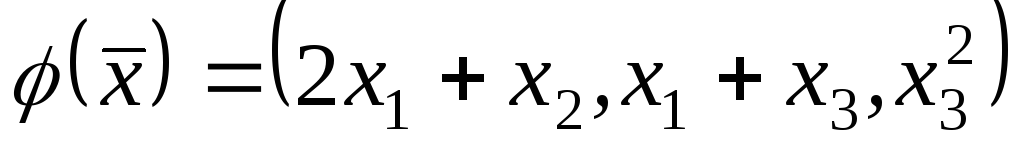 ;
;2)
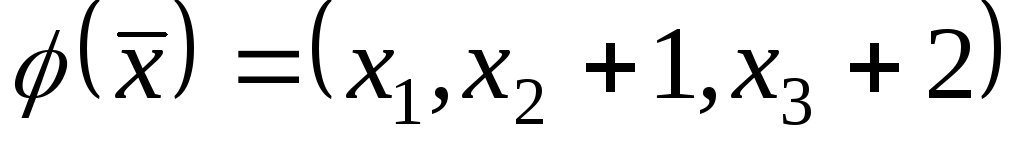 ;
;6)
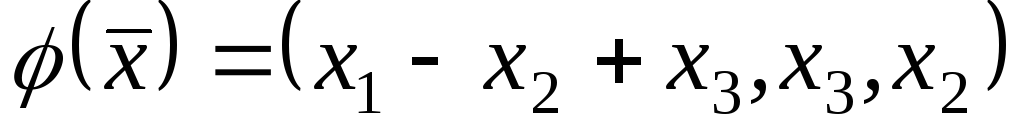 ;
;3)
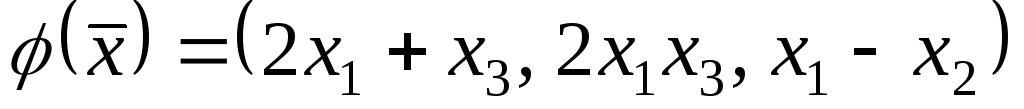 ;
;7)
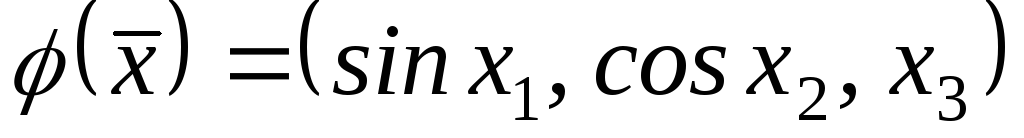 ;
;4)
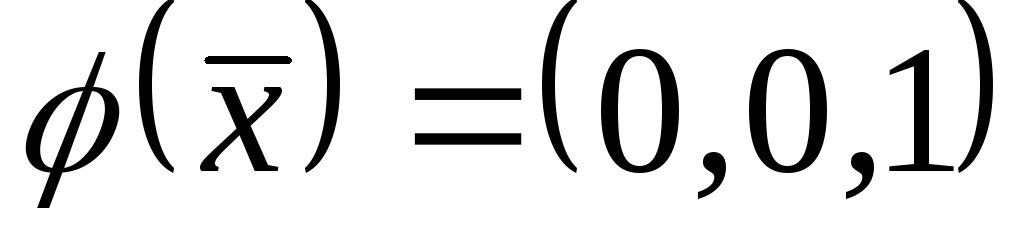 ;
;8)
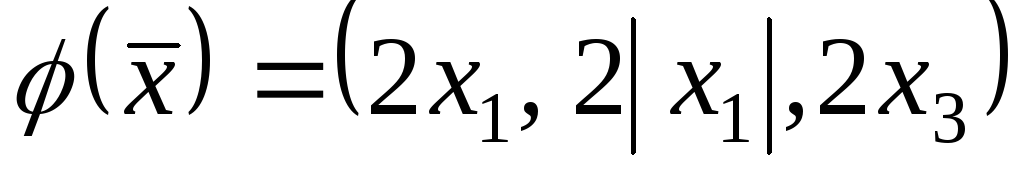 .
.Нехай
 – довільний вектор,
– довільний вектор, – фіксований ненульовий вектор
геометричного векторного простору
(двовимірного або тривимірного).
Перевірте на лінійність перетворення
– фіксований ненульовий вектор
геометричного векторного простору
(двовимірного або тривимірного).
Перевірте на лінійність перетворення ,
заданого наступною формулою, та зясуйте
його геометричний зміст, якщо:
,
заданого наступною формулою, та зясуйте
його геометричний зміст, якщо:
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
Лінійний оператор
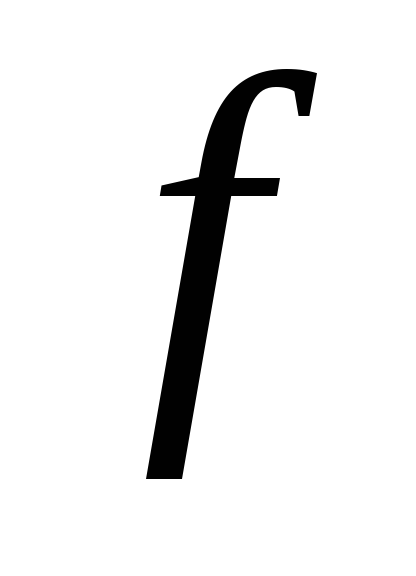 заданий в базисі
заданий в базисі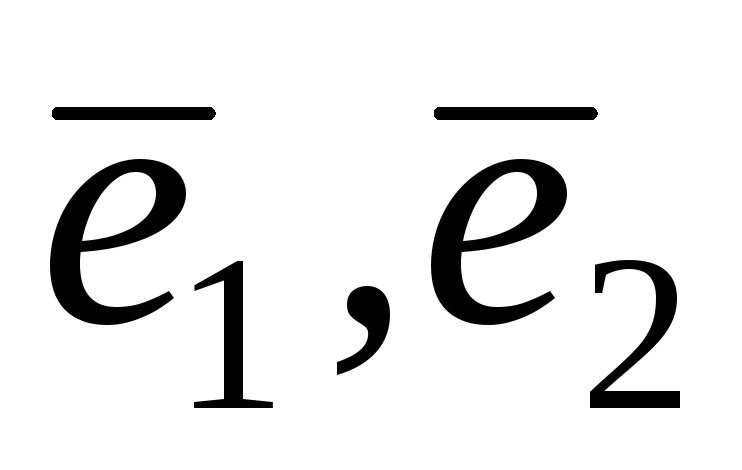 матрицею
матрицею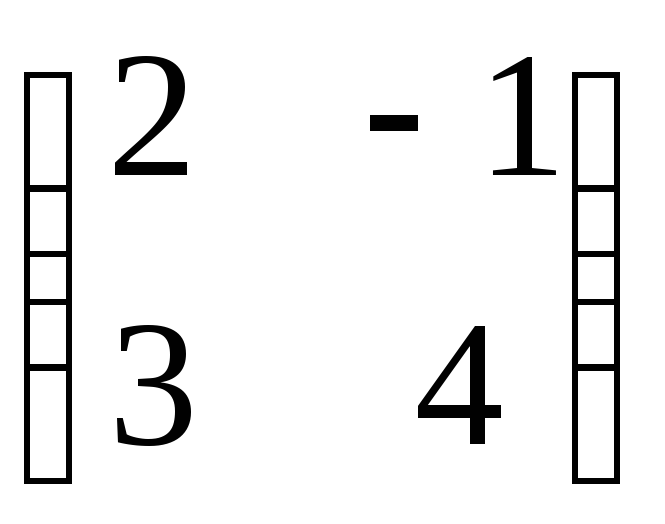 .
Знайдіть його матрицю в базисі
.
Знайдіть його матрицю в базисі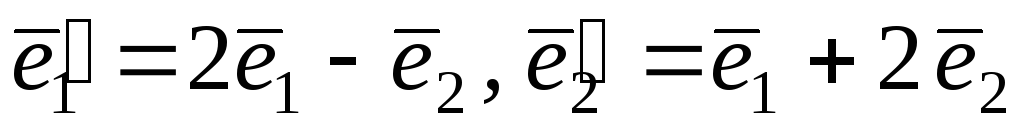 .
.Лінійний оператор
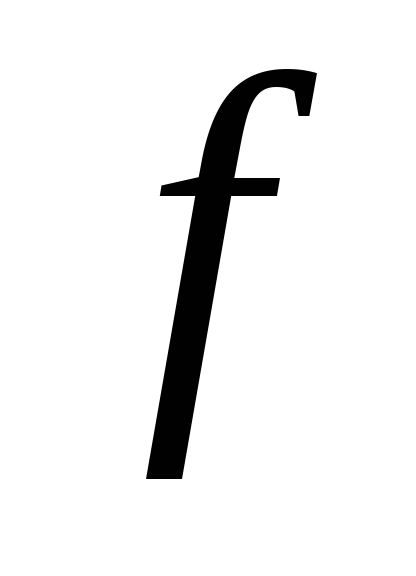 заданий в базисі
заданий в базисі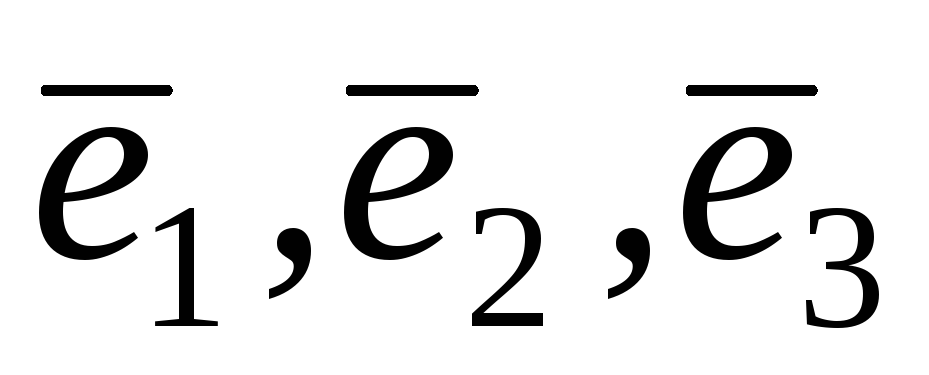 матрицею
матрицею .
Знайдіть його матрицю в базисі
.
Знайдіть його матрицю в базисі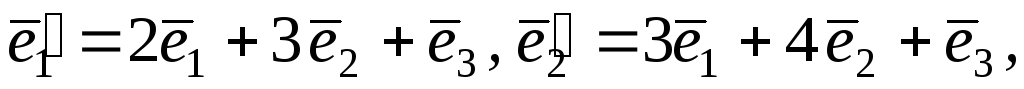
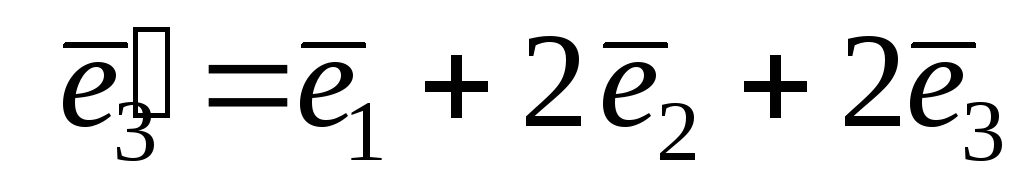 .
.Лінійний оператор
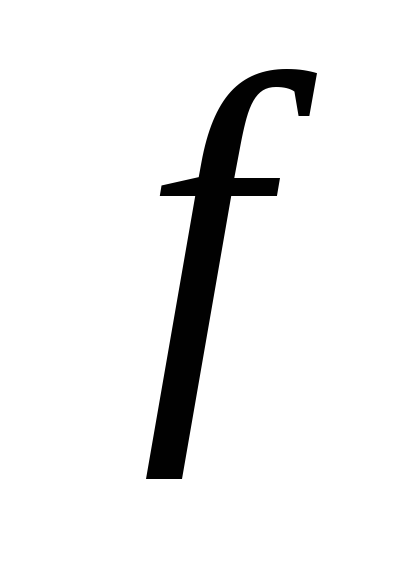 заданий в базисі
заданий в базисі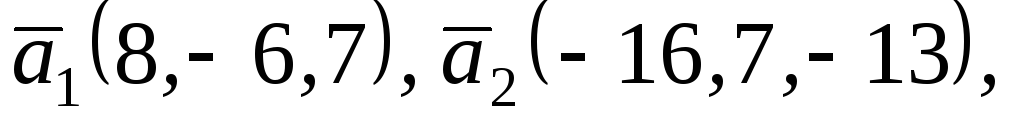
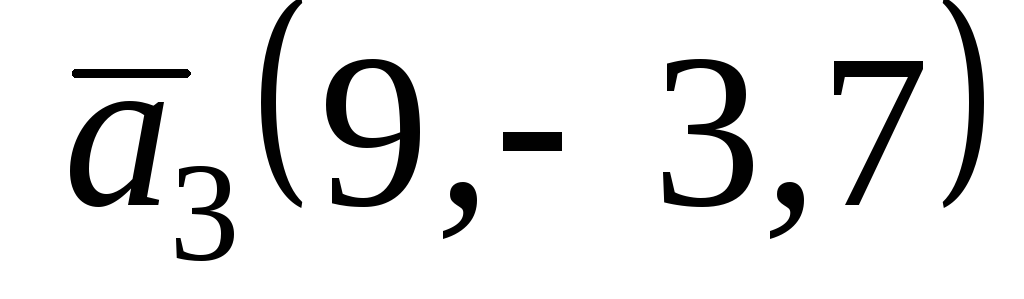 матрицею
матрицею
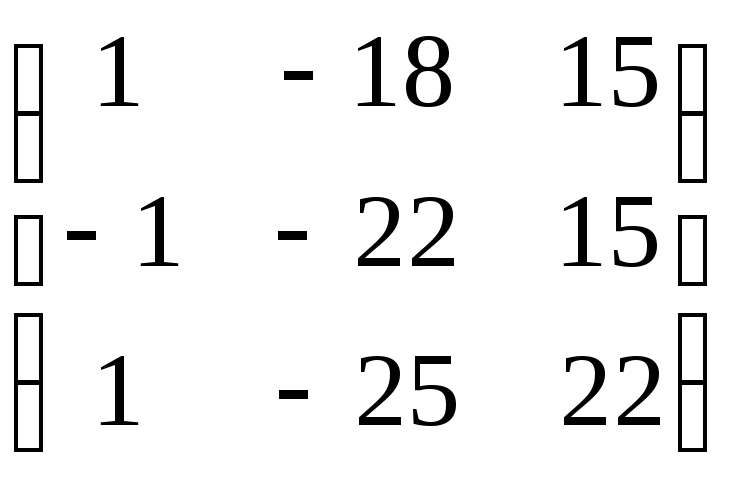 .
Знайдіть його матрицю в базисі
.
Знайдіть його матрицю в базисі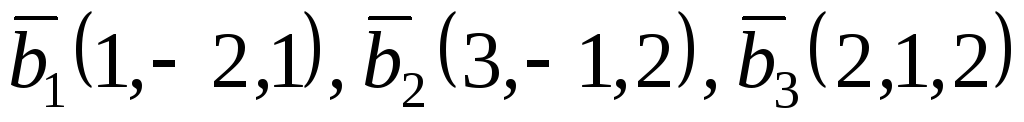 .
.В базисі
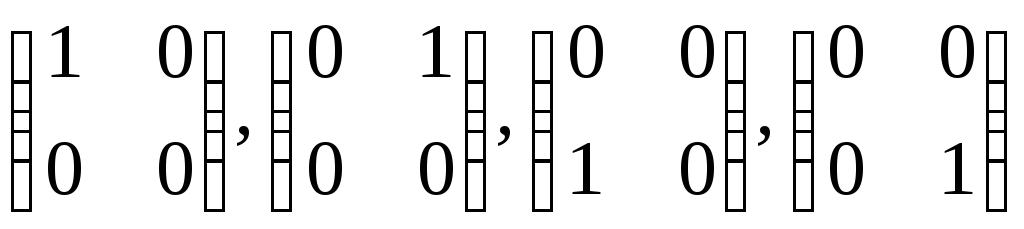 простору матриць другого порядку
лінійний оператор заданий матрицею
простору матриць другого порядку
лінійний оператор заданий матрицею .
Знайдіть матрицю цього оператора в
базисі
.
Знайдіть матрицю цього оператора в
базисі .
.В базисі
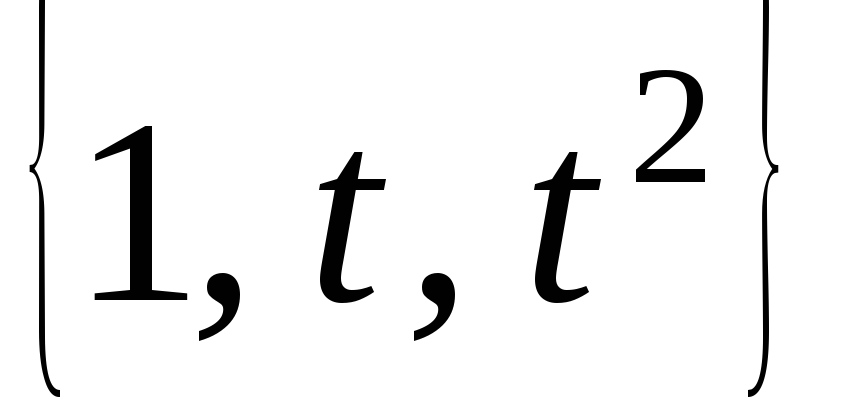 простору
простору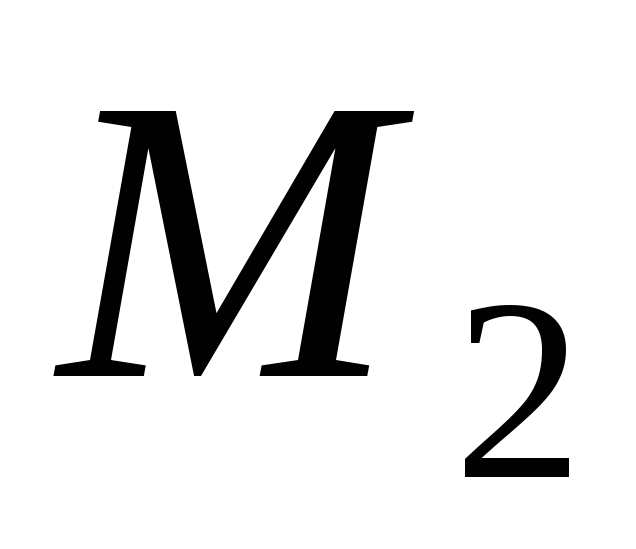 оператор
оператор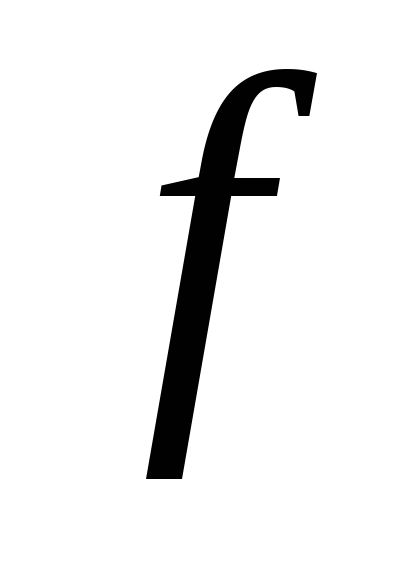 заданий матрицею
заданий матрицею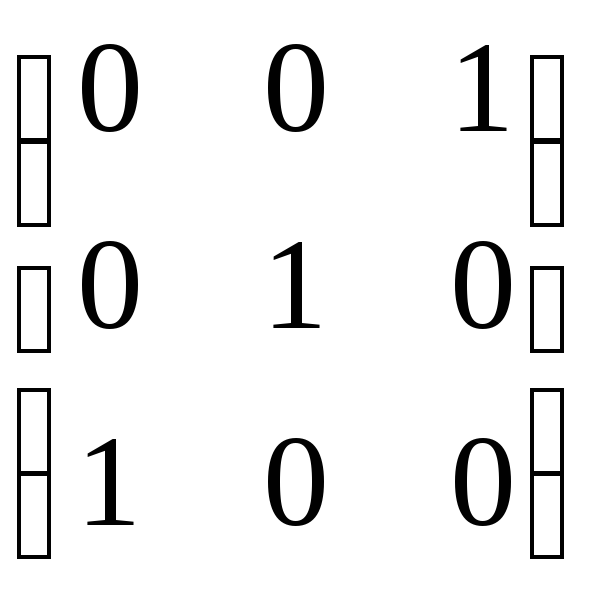 .
Знайдіть матрицю цього оператора в
базисі:
.
Знайдіть матрицю цього оператора в
базисі:
1)
![]() ;
;
2)
![]() .
.
Лінійний оператор
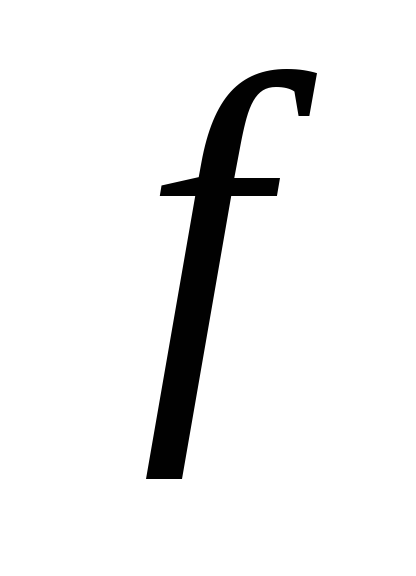 в базисі
в базисі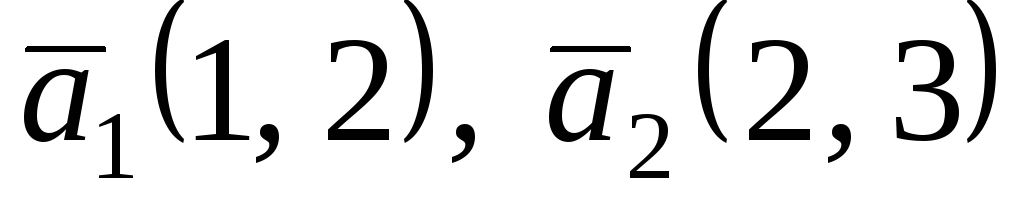 заданий матрицею
заданий матрицею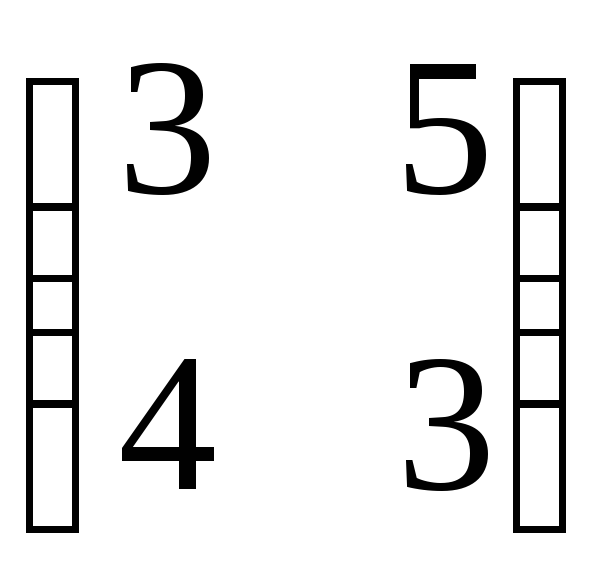 ,
а лінійний оператор
,
а лінійний оператор в базисі
в базисі
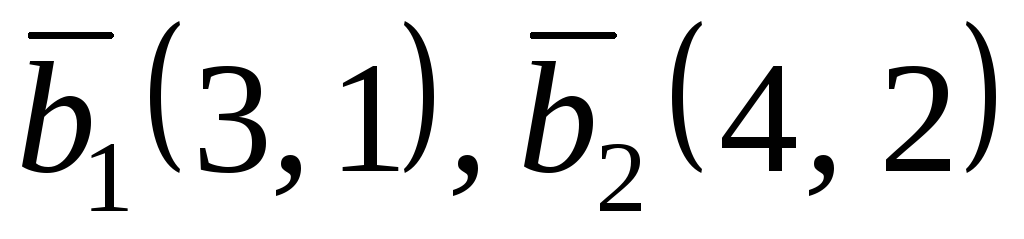 – матрицею
– матрицею
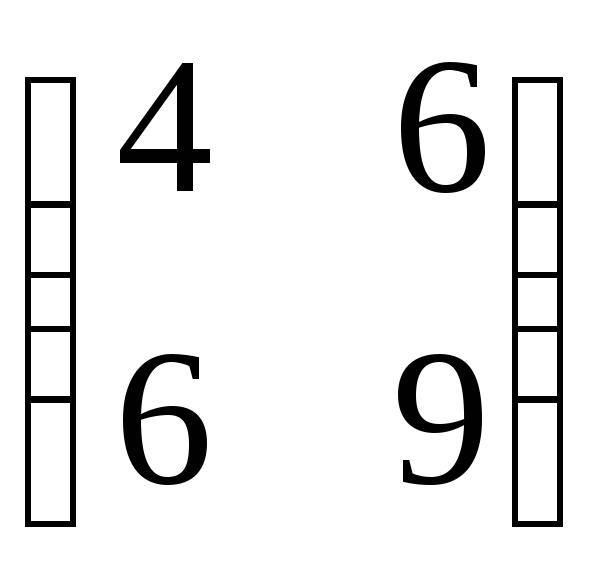 .
Знайдіть матрицю оператора
.
Знайдіть матрицю оператора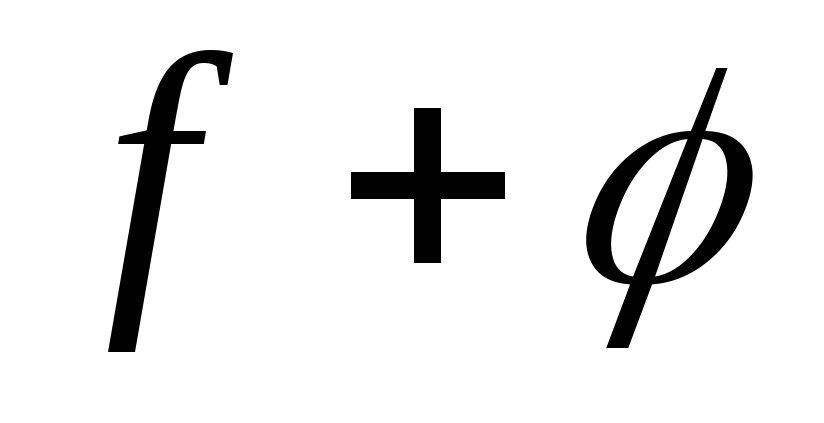 в базисі
в базисі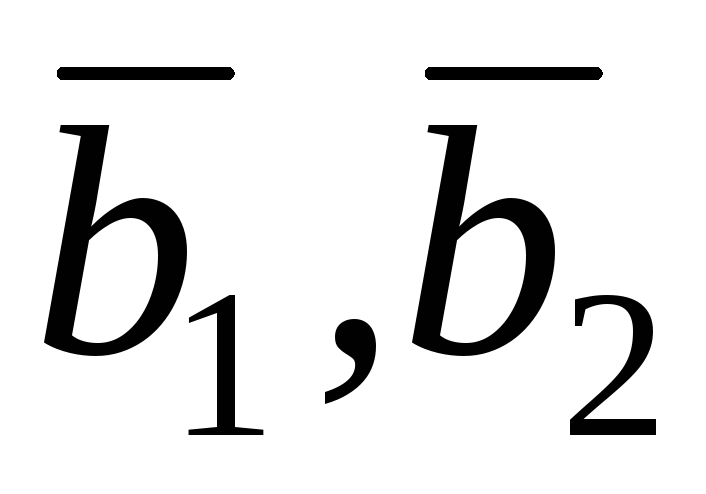 .
.Знайдіть образ та ядро лінійного оператора
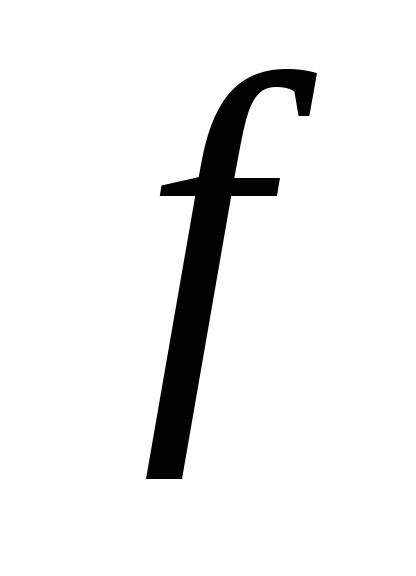 дійсного лінійного простору
дійсного лінійного простору вільних векторів, якщо:
вільних векторів, якщо:
1)
![]() ;
2)
;
2)![]() ,
де
,
де![]() – задані ненульові вектори.
– задані ненульові вектори.
Для вказаних операторів простору
 знайдіть ранг, дефект, а також побудуйте
базис образу та ядра. Кожен оператор
задається своєю дією на довільному
векторі
знайдіть ранг, дефект, а також побудуйте
базис образу та ядра. Кожен оператор
задається своєю дією на довільному
векторі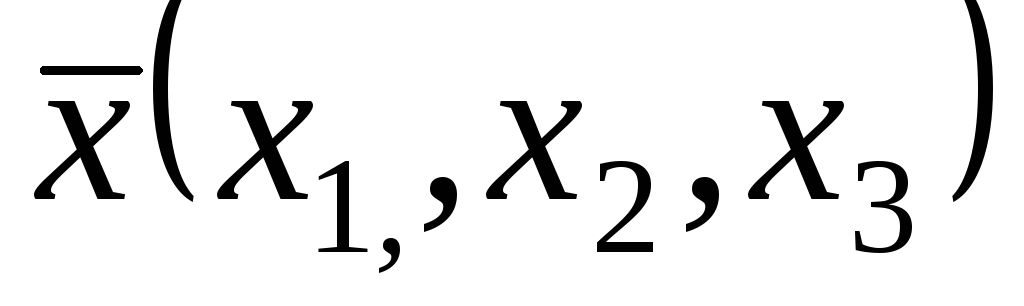 :
:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() .
.
Знайдіть базис образу та базис ядра лінійного оператора
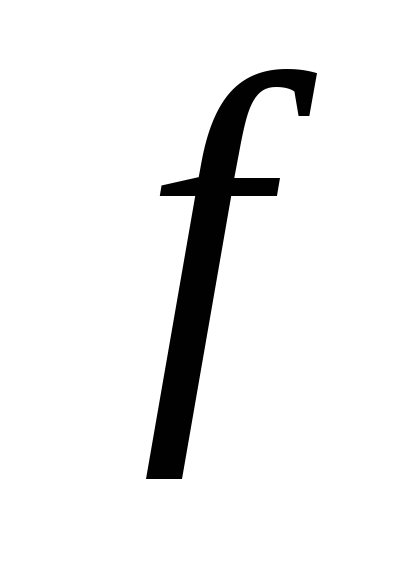 простору
простору ,
заданого у деякому базисі матрицею
,
заданого у деякому базисі матрицею :
:1)
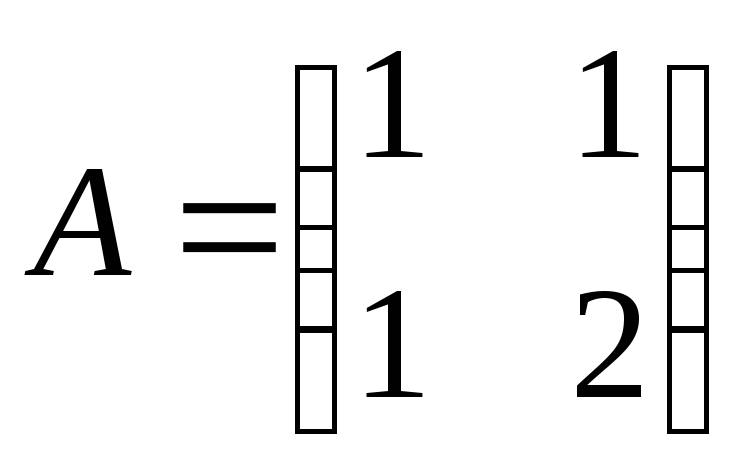 ;
;3)
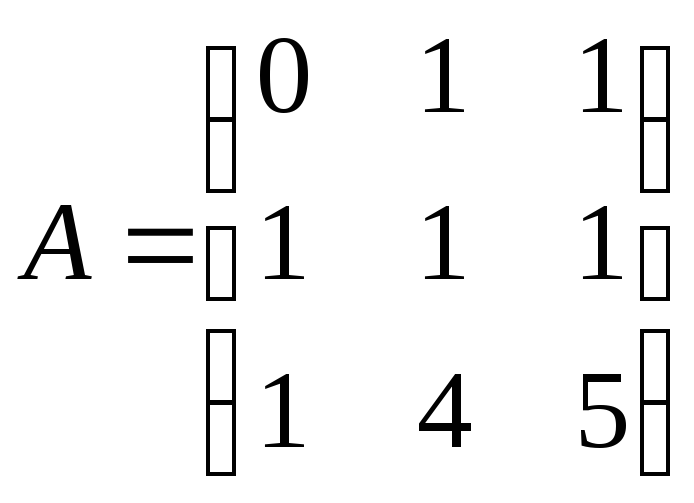 ;
;5)
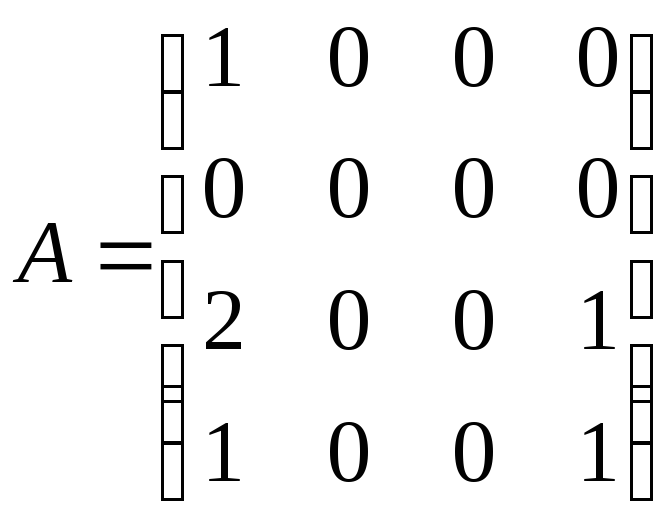 ;
;2)
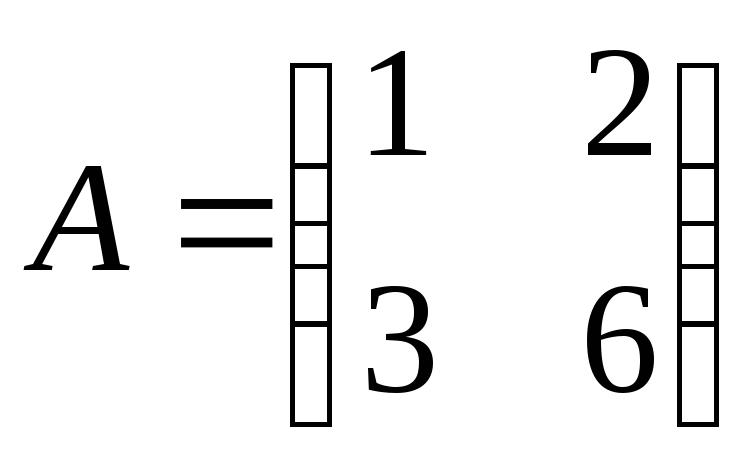 ;
;4)
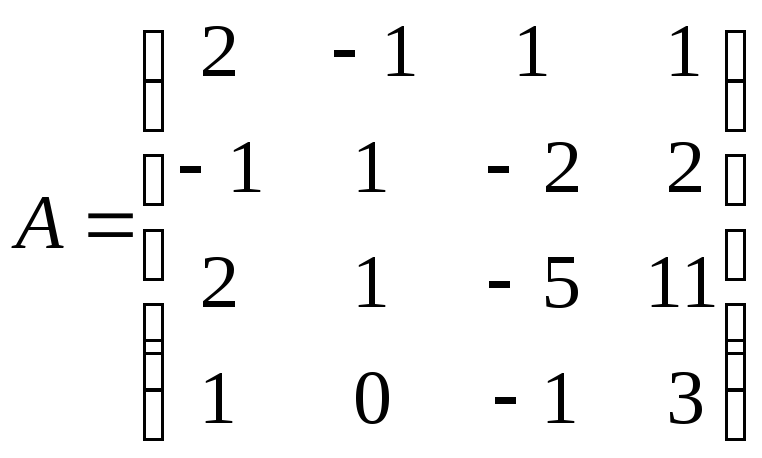 ;
;6)
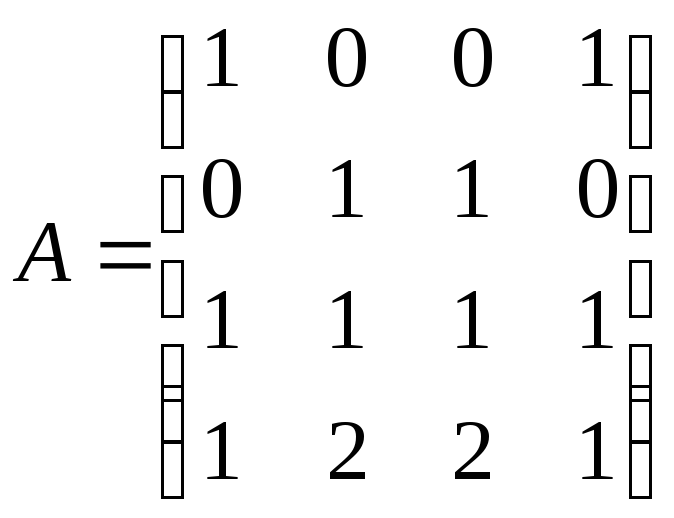 .
.Знайдіть власні значення та власні вектори лінійних операторів, що задані у деякому базисі лінійного простору: а) над
 ;
б) над
;
б) над ;
в) над
;
в) над :
:1)
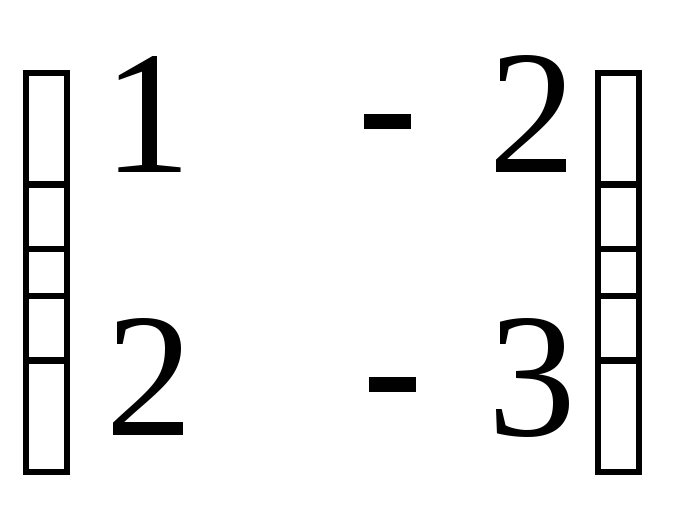 ;
;5)
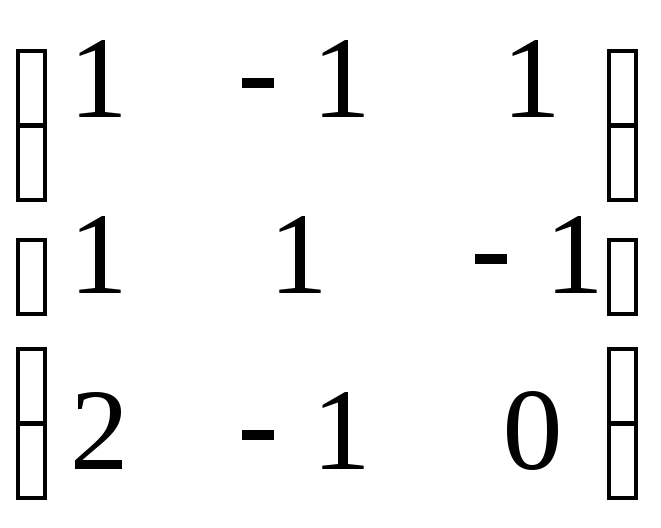 ;
;9)
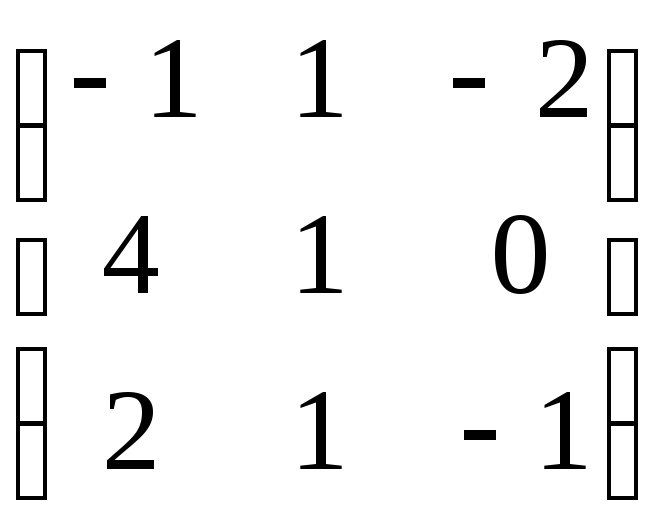 ;
;2)
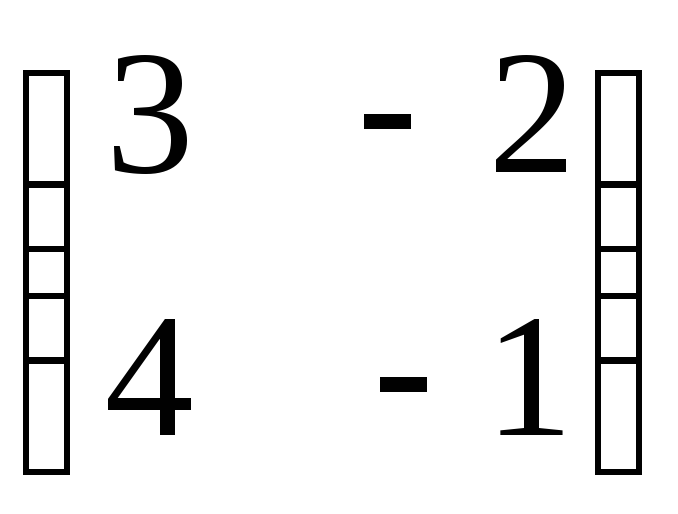 ;
;6)
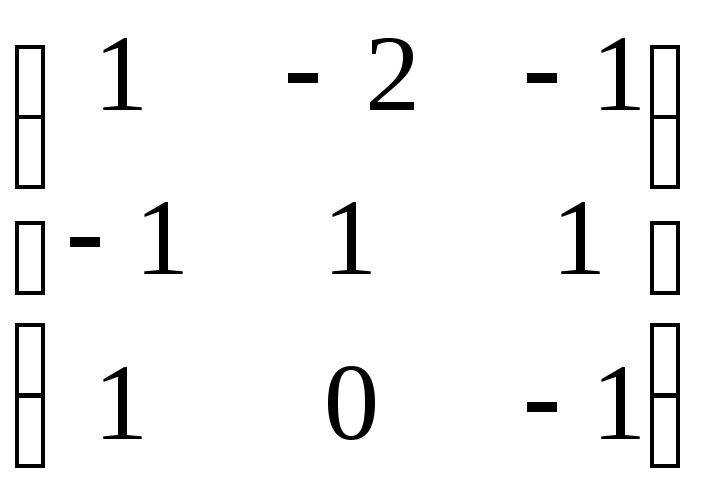 ;
;10)
 ;
;3)
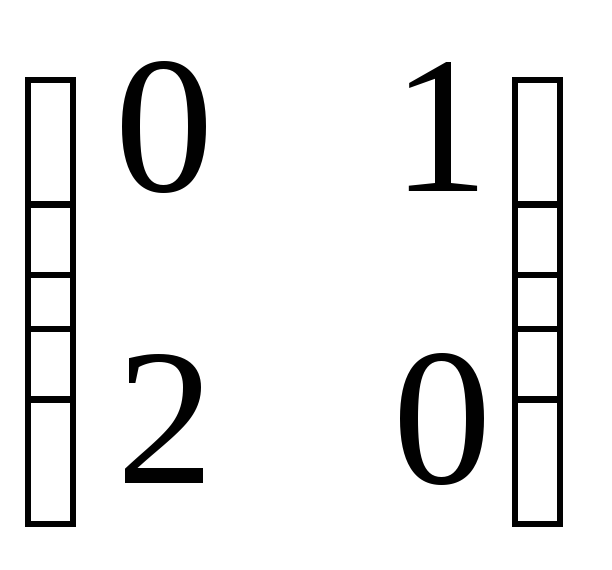 ;
;7)
 ;
;11)
 ;
;4)
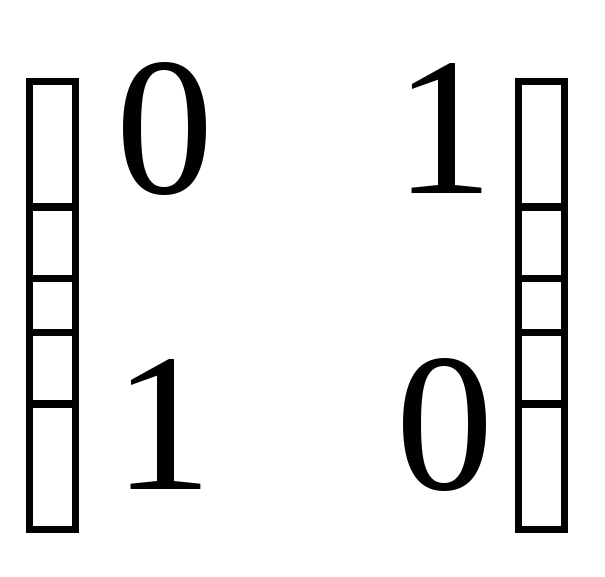 ;
;8)
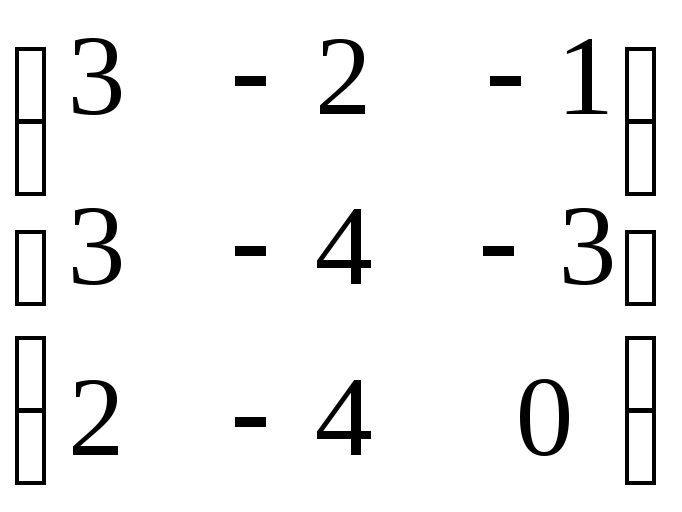 ;
;12)
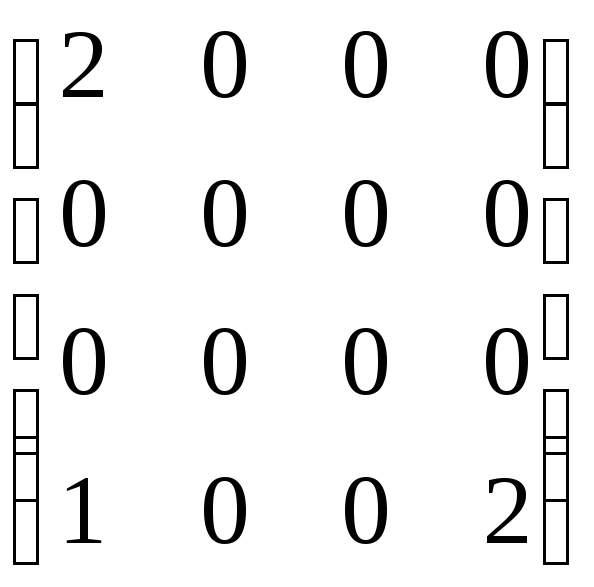 .
.З’ясуйте, які з матриць лінійних операторів у просторі
 над
над можна звести до діагонального виду
шляхом переходу до нового базису.
Знайдіть цей базис та відповідну йому
матрицю:
можна звести до діагонального виду
шляхом переходу до нового базису.
Знайдіть цей базис та відповідну йому
матрицю:1)
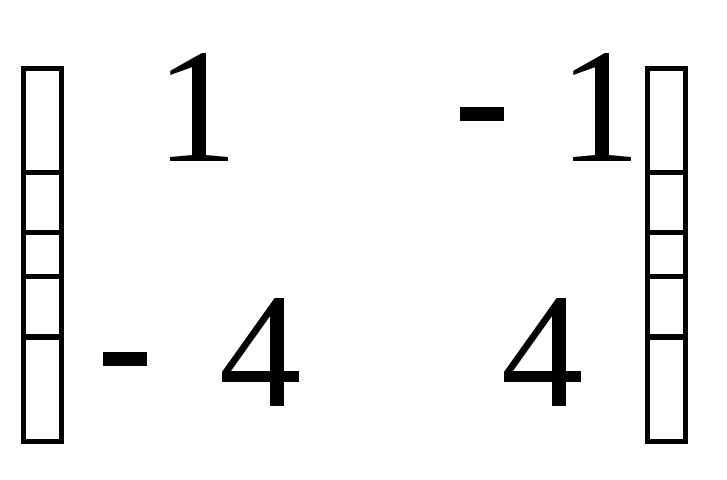 ;
;3)
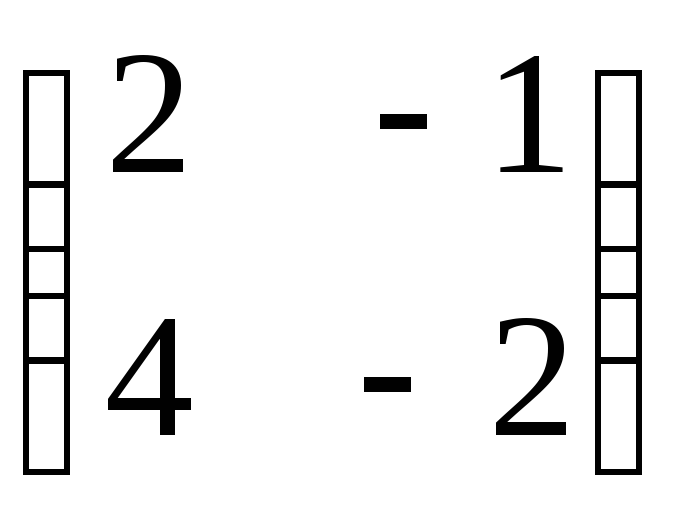 ;
;5)
 ;
;2)
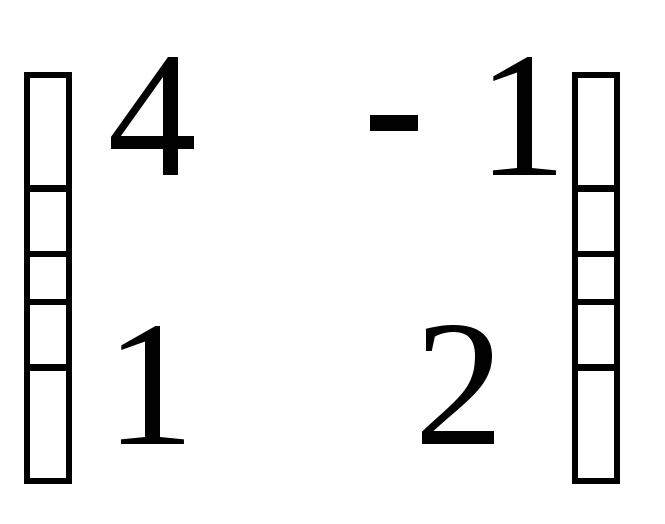 ;
;4)
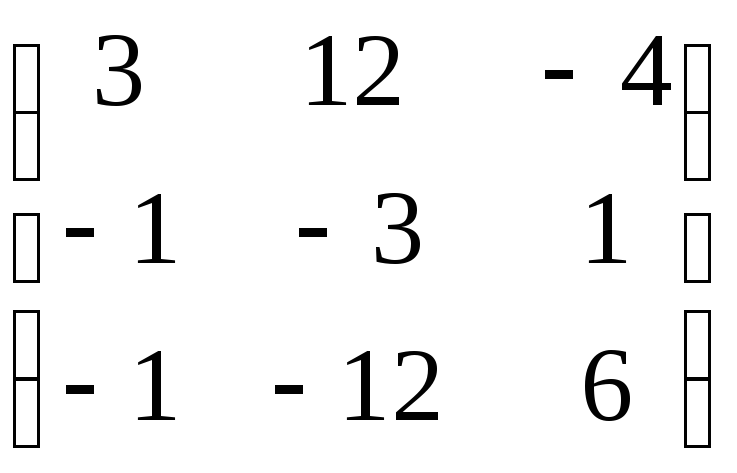 ;
;6)
 .
.Знайдіть всі підпростори тривимірного простору, які є інваріантними відносно лінійного оператору, заданого матрицею:
1)
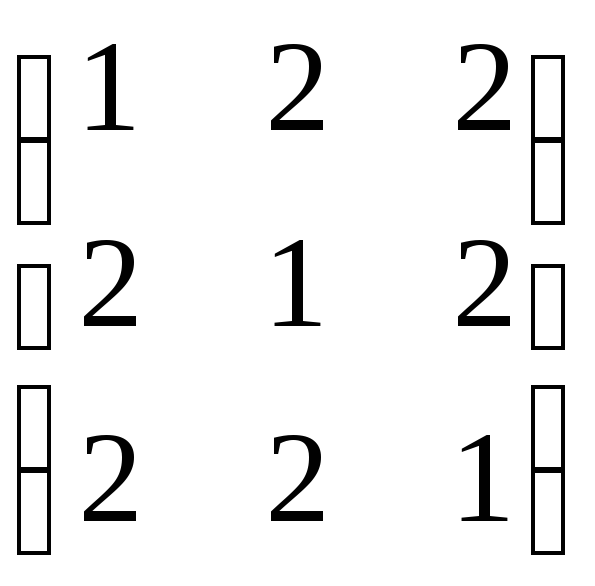 ;
;2)
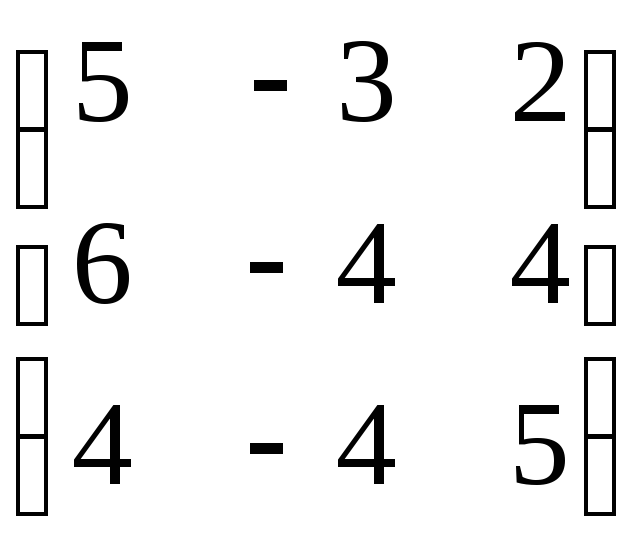 ;
;3)
 ;
;4)
 .
.Знайдіть канонічний базис відносно нильпотентного оператору та його матрицю у цьому базисі, якщо оператор заданий матрицею у деякому базисі:
1)
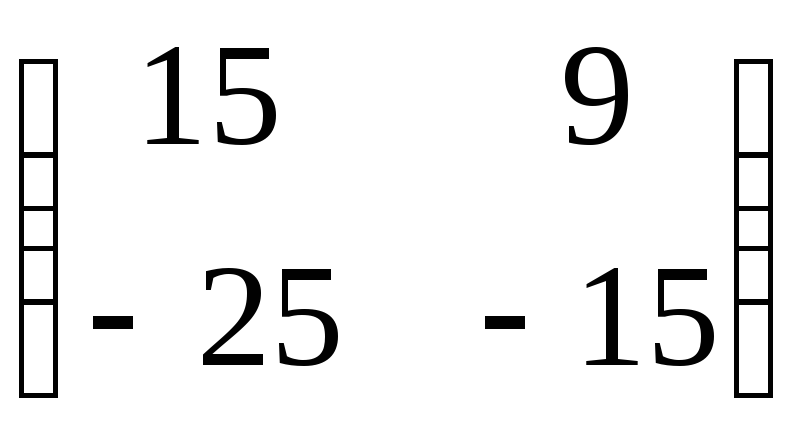 ;
;2)
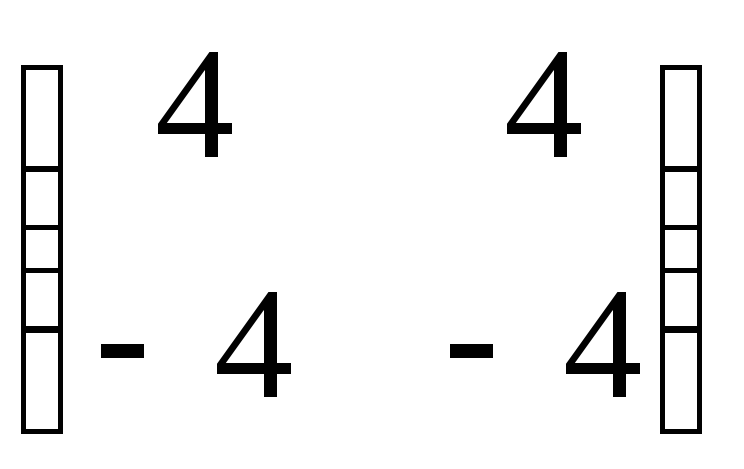 ;
;3)
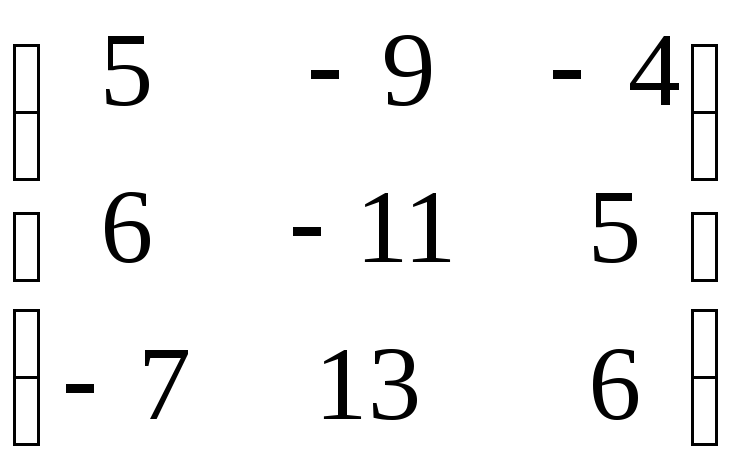 ;
;4)
 .
.Знайдіть жорданову форму, мінімальний многочлен, систему елементарних дільників, а також форму Фробеніуса матриці:
1)
 ;
;2)
 ;
;3)
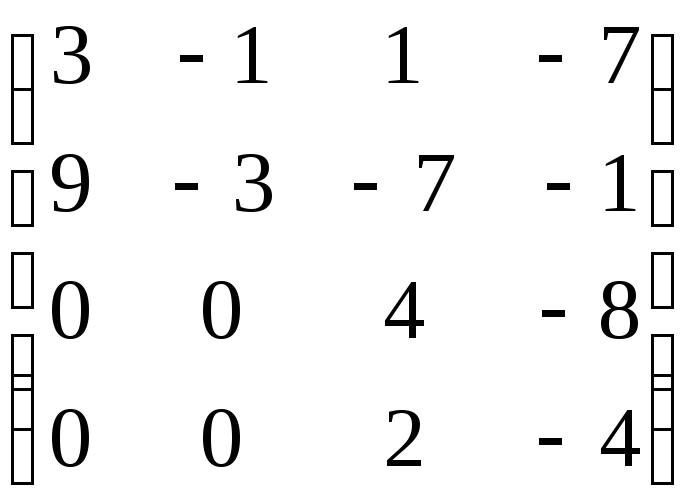 .
.Знайдіть жорданову форму матриці:
1)
 ;
;2)
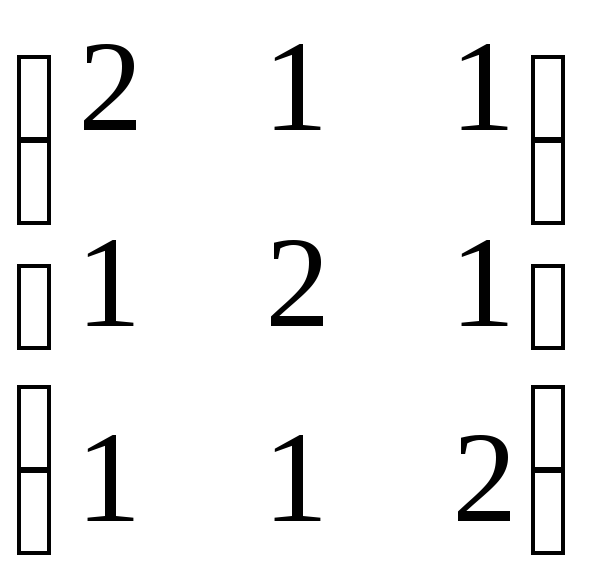 ;
;3)
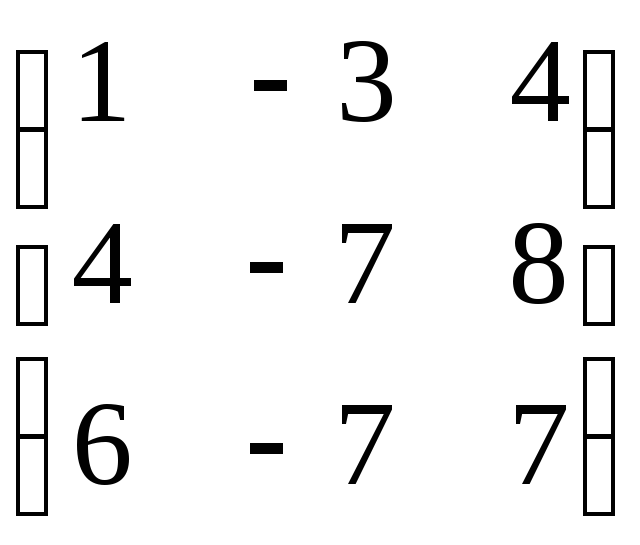 ;
;4)
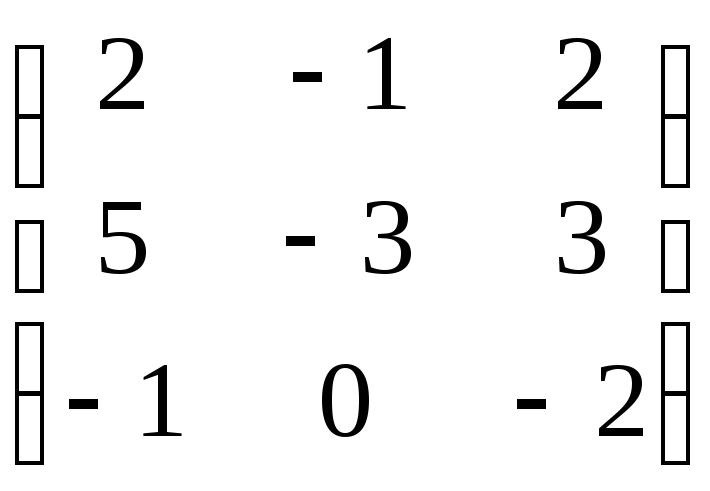 .
.З’ясуйте, чи подібні матриці:
1)
![]() та
та![]() ;
;
2)
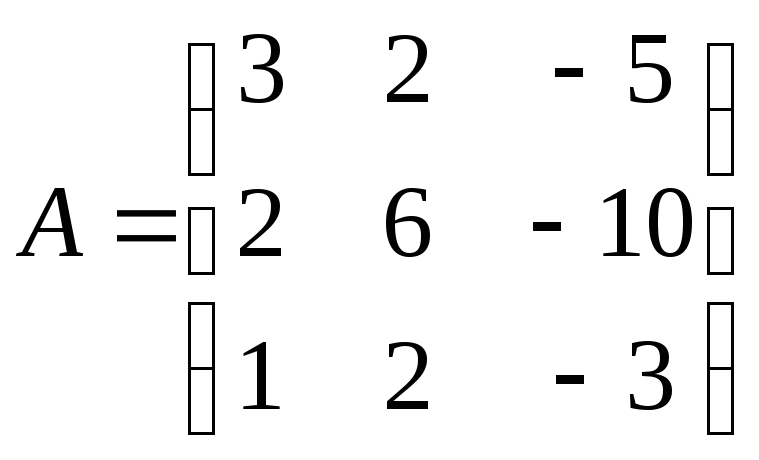 та
та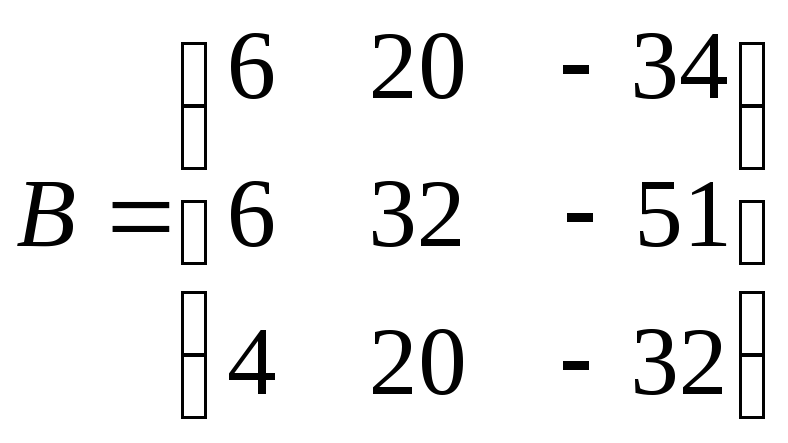 ;
;
3)
 та
та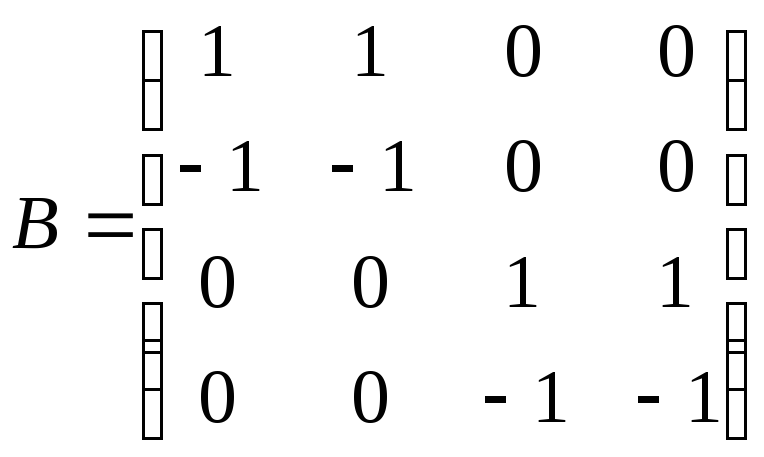 .
.
