7.2. Метод Ньютона (дотичних)

Цей метод дуже ефективний для розв’язання алгебраїчних і трансцендентних рівнянь. Його основна перевага полягає в тому, що при порівняно простій схемі обчислень він має швидку збіжність.

Нехай єдиний корінь рівняння

(1)

розташований усередині інтервалу , причомуінеперервні і зберігають визначені знаки. Відповідно до методу Ньютона корінь вихідного рівняння відшукується як границя ітераційної послідовності

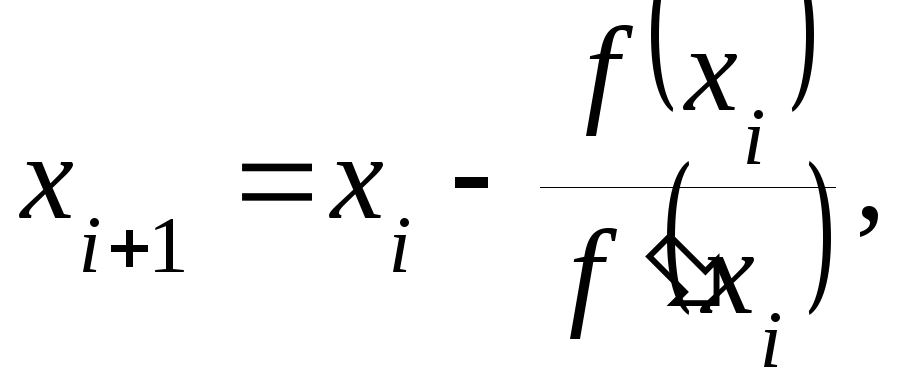
. (2)

Початкове наближення і повинне задовольняти умові

. (3)

Геометрично метод Ньютона еквівалентний заміні рівняння кривої рівнянням дотичної, проведеної до цієї кривої в точці. За наближене значення кореня береться абсциса точки перетину цієї дотичної з віссю.

Для оцінки точності наближенняможна скористатися формулою

, (4)

де ,, (5)

– точне значення кореня.

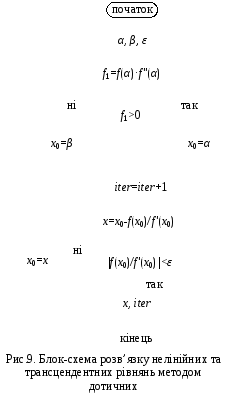
На рис. 9 наведено блок-схему програми розв’язку нелінійних та трансцендентних рівнянь методом дотичних.

У даній блок-схемі: α – лівий кінець інтервалу; β – правий кінець інтервалу; ε – точність обчислень; x₀ – корінь рівняння на попередній ітерації; x – корінь рівняння на поточній ітерації; iter – номер ітерації; f(x) – значення функції у точці x.

Знайдемо, наприклад, з точністю корінь рівняння. Виконавши процедуру відділення коренів так, як описано вище (див. Розділ 3. Загальні положення) одержимо три інтервали,,, що містять корінь. Знайдемо корінь, розташований в інтервалі. Цей інтервал методом бісекції зменшимо так, щоб його довжина була.

Маємо:

;

;

;

;

.

Довжина отриманого інтервалу

.

Подальше уточнення кореня проведемо методом Ньютона.

Друга похідна на цьому інтервалі більше нуля, перша похідна– менше нуля. За початкове наближеннявізьмемо лівий кінець інтервалу, тобто. Тоді

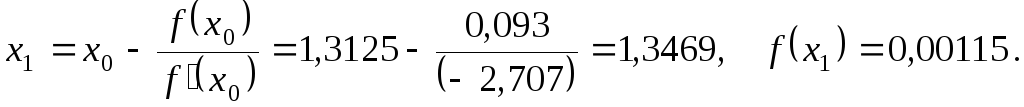
Обчислимо значення першої похідної на другому кінці інтервалу й оцінимо похибку отриманого наближення, тобто.

.

Точність, з якою обчислене перше наближення, недостатня. Тому робимо наступний крок

,

.

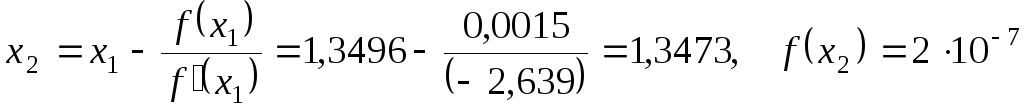Як видно з оцінки похибки другого наближення, ми одержали значення кореня з похибкою, що не перевищує задану.

Корені, розташовані в двох інших інтервалах ,знаходяться аналогічно.

Питання для самоперевірки

1. Сформулюйте постановку задачі, опишіть метод Ньютона.

2. Наведіть формулу для контролю похибки методу Ньютона.

3. Дайте геометричну інтерпретацію методу.

4. В чому полягає умова вибору нульового наближення?

7.3. Метод пропорційних частин (хорд)

Розрахункові формули цього методу отримані з таких міркувань. Інтервал , усередині якого розташований корінь рівняння

, (1)

ділимо у відношенні . Це дасть нам наближене значення кореня, де

, . (2)

Далі, застосовуючи цей прийом до одного з відрізків чи, на кінцях якого функціямає протилежні знаки, одержимо друге наближенняі т.д.

Геометрично спосіб пропорційних частин еквівалентний заміні рівнянь кривої рівнянням хорди, що проходить через точкиі. За наближене значення кореня приймається абсциса точки перетину хорди з віссю.

Уточнення кореня варто проводити доти, поки не буде досягнута задана точність. Для оцінки точності наближення можна скористатися формулою

,

де ,, (3)

– точне значення кореня.

На рис. 10 наведено блок-схему програми розв’язку нелінійних та трансцендентних рівнянь методом хорд.

У даній блок-схемі: α – лівий кінець інтервалу; β – правий кінець інтервалу; ε – точність обчислень; x₀ – корінь рівняння на попередній ітерації; x – корінь рівняння на поточній ітерації; iter – номер ітерації; f(x) – значення функції у точці x.

Наприклад, знайдемо з точністю до корені рівняння. Виконавши процедуру відділення коренів так, як описано вище (див. Розділ 3. Загальні положення) одержимо три інтервали,,, що містять корінь. Знайдемо корінь, розташований в інтервалі.

Маємо ,,.

Від нескінченного інтервалу перейдемо до скінченого, замінивши його ліву границю скінченим числом менше нуля, але таким, щоб значення функції в ньому було від’ємним. Інтервал задовольняє цим вимогам:. Крім того,на цьому інтервалі знакопостійна і, отже,– монотонна й досягає найбільшого й найменшого значення на кінцях інтервалу. Використовуючи метод бісекції, зменшимо цей інтервал так, щоб його довжина була.

Маємо:

корінь ;

корінь ;

корінь ;

корінь ;

Довжина отриманого інтервалу , тому надалі будемо працювати з цим інтервалом.

Обчислюючи значення першої похідної на кінцях інтервалу, одержуємо;. Отже, у формулі для оцінки похибки якможна прийняти.

Оскільки друга похідна на обраному інтервалі від’ємна, то як нерухомий кінець у формулі для обчислення кореня за методом хорд варто взяти лівий кінець інтервалу, тобто розрахункова формула набуде вигляду:

, ,

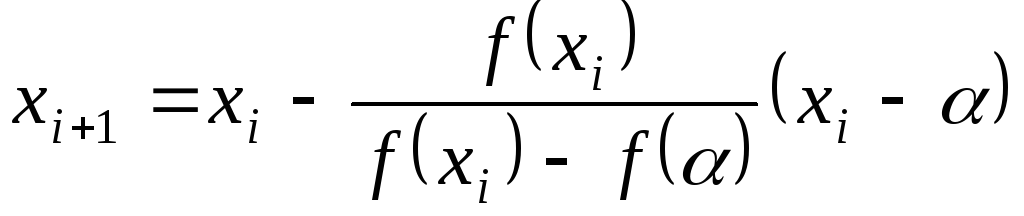де ,.

Виконуючи розрахунок за цією формулою при , одержимо,.

Обчислимо похибку

.

Таким чином, уже перше наближення дає значення кореня з потрібною точністю.

Корені, розташовані в двох інших інтервалах ,знаходяться аналогічно.