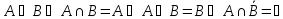Дискретная Математика / Lektsia_2_Mnozhestva
.docxЛекция №2
Тема лекции: Множества.
Содержание:
-
Основные понятия и определения.
-
Способы задания множеств.
-
Пустое множество.
-
Операции над множествами.
-
Универсум множества.
-
Свойства множеств.
-
Множество подмножеств.
-
Алгебра множеств.
-
Обобщение операций над множествами.
Основные понятия теории множеств
Множество – объединение объектов, хорошо различаемых нашей интуицией или нашей мыслью, в единое целое. Георг Кантор.
«Множество образуется из элементов, обладающих некоторыми свойствами и находящихся в некоторых отношениях между собой или с элементами других множеств» Н. Бурбаки.
Объекты, образующие множество, называются элементами множества.
Обозначение конкретных множеств таково:

Обозначение элементов множеств:

Примеры множеств:
-
Множество натуральных чисел.
-
Множество цифр десятичной системы.
-
Множество цифр двоичной системы.
-
Множество чётных чисел.
-
Множество страниц книги.
-
Множество студентов университета.
Способы задания множеств
-
Вербальный (словесный) – путём описания характеристических свойств, которыми должны обладать элементы множеств. Например, «множество цифр двоичной системы».
-
Задание списком (перечислением) всех элементов. Даётся в фигурных скобках.
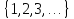


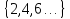
-
Предикатный (высказывательный, порождающий). Задаётся с помощью предиката, т.е. множество задаётся в виде {x:P(x)} или {x|P(x)}, где Р(х) принимает значение «истина» для элементов множества.
{1,2,3,…}={x|x – натуральное число}
{0,1,2,…,9}={x|x – цифра десятичной системы}
{0,1}={x|x – цифра двоичной системы}
{2,4,6,…}={x|x – чётное число}
-
Анатомический – с помощью аналитического выражения, формулы.
 (x
принадлежит множеству S)
(x
принадлежит множеству S)
 (x
– не принадлежит множеству S)
(x
– не принадлежит множеству S)
 -
символ принадлежности элемента к
множеству.
-
символ принадлежности элемента к
множеству.
Пустое множество
Множество,
которое не содержит элементов, пустое
 .
.
S={x|x
– нечётное число, делящееся на 2}=
Пустое
множество – совокупность объектов, ни
один из которых не принадлежит множеству
 .
.
Для любого А справедливо

Множество
 в
множество А.
в
множество А.
Операции над множествами
Объединение
А и В
( )
– это множество, состоящее из всех
элементов множества А, всех элементов
множества В и не содержащее никаких
других элементов, т.е.
)
– это множество, состоящее из всех
элементов множества А, всех элементов
множества В и не содержащее никаких
других элементов, т.е.
 ,
где знак
,
где знак
 обозначает логическую операцию конъюнкция
(логическое «и»).
обозначает логическую операцию конъюнкция
(логическое «и»).

Пересечение
А и В ( )
– это множество, состоящее из тех и
только тех элементов, которые принадлежат
одновременно множеству А и множеству
В, т.е.
)
– это множество, состоящее из тех и
только тех элементов, которые принадлежат
одновременно множеству А и множеству
В, т.е.
 ,
где
,
где
 знак
"обозначает логическую операцию
дизъюнкция" ("логическое или"
).
знак
"обозначает логическую операцию
дизъюнкция" ("логическое или"
).

Разность
А и В
(относительное дополнение) – это
множество, состоящее из тех и только
тех элементов, которые принадлежат А и
не принадлежат В, т.е.
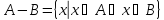

Дизъюнктивная
сумма А и В
(или симметричная разность) – это
множество, состоящее из всех элементов
А, не принадлежащих В, а так же всех
элементов В, не принадлежащих А, и не
содержащее накаких других элементов,
т.е.


Универсум
Совокупность всех допустимых объектов называется основным множеством (универсумом) и обозначается U.
Универсум U арифметики – числа, универсум U зоологии – животные и т.д.

Любое множество будем рассматривать в связи с универсумом, который на кругах Эйлера будем ассоциировать с прямоугольником на плоскости, внутри которого будем изображать множества

Новая
операция
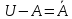 (абсолютное дополнение А) – это множество,
которое содержит все элементы универсума.
За исключением элементов А.
(абсолютное дополнение А) – это множество,
которое содержит все элементы универсума.
За исключением элементов А.
Множество подмножеств
Определение. Множество А называется подмножеством В, если каждый элемент А является элементом В.
Для
обозначения этого факта вводится значок
« »
- символ включения (или «
»
- символ включения (или « »)
»)
 другими
словами
другими
словами
 .
.
Определение. Два множества равны, если они состоят из одних и тех же элементов А=В.
Определение.
Множество,
элементами котрого являются все
подмножества множества
А, называют множеством подмножеств
(множеством - степенью) множества А и
обозначается Р(А). Так, для трехэлементного
множества
 имеем
имеем

Основные свойства операций над множествами
|
Коммутативный закон |
А |
|
|
А |
|
Ассоциативный закон |
А |
|
|
А |
|
Дистрибутивный закон |
А |
|
|
А |
|
Свойства
|
А |
|
|
А |
|
|
А |
|
|
А |
|
|
А |
|
|
А |
|
|
|
|
|
|
|
Закон идемпотентности |
А |
|
(самопоглощения) |
А |
|
Закон поглощения |
А |
|
|
А |
|
Теорема де Моргана |
|
|
|
|
|
Свойства дополнения, |
|
|
разности и равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основное содержание лекции
Множество образуется из элементов, обладающих некоторыми свойствами и находящихся в некоторых отношениях между собой или с элементами других множеств. Н. Бурбаки

 В=В
В=В А
А
 В
= В
В
= В А
А
 (В
(В С)
= (А
С)
= (А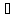 В)
В) С
С (В
(В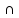 С)
= (А
С)
= (А В)
В) С
С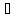 (В
(В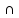 С)
= (А
С)
= (А В)
В) (А
(А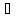 С)
С) (В
(В С)
= (А
С)
= (А В)
В) (А
(А С)
С) и
U
и
U = А
= А = А
= А =U
=U = 0
= 0 U
=U
U
=U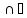 =
=

 =
U
=
U =
=

 А
= А
А
= А А
= А
А
= А (А
(А В)
= А
В)
= А (А
(А В)
= А
В)
= А =
=
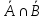
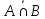 =
=


 =
А
=
А