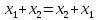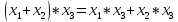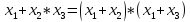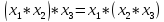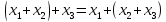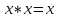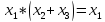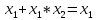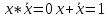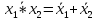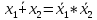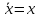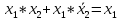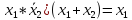Дискретная Математика / Lektsia_7_Tozhdestva_algebry_logiki
.docxЛекция №7
Тема: Тождества алгебры логики.
Содержание
-
Равносильность алгебры логики.
-
Основные тождества алгебры логики.
-
Таблица основных тождеств.
-
Правила «основных тождеств».
-
Примеры преобразования в алгебре логики.
Равносильность формул
Формулы
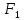 и
и
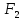 называются равносильными, если при
любых значениях входящих в них переменных
называются равносильными, если при
любых значениях входящих в них переменных
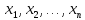 эти формулы принимают одинаковые
значения.
эти формулы принимают одинаковые
значения.
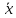 равносильно
х
равносильно
х
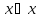 равносильно
х
равносильно
х
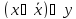 равносильно
у
равносильно
у
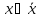 равносильно
равносильно
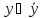 .
.
Между
понятиями равносильности и эквивалентности
существует связь: если формулы
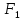 и
и
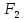 равносильны, то формула
равносильны, то формула
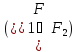 (эквивалентность) принимает одни и те
же значения при всех значениях переменных
и обратно: если формула
(эквивалентность) принимает одни и те
же значения при всех значениях переменных
и обратно: если формула
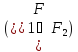 принимает одни и те же значения при всех
значениях переменных, то формулы
принимает одни и те же значения при всех
значениях переменных, то формулы
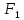 и
и
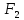 равносильны.
равносильны.
Примеры равносильных формул:
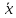 равносильно
х
равносильно
х
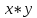 равносильно
у*х
равносильно
у*х
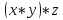 равносильно
x*(y*z)
равносильно
x*(y*z)
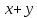 равносильно
равносильно
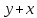 .
.
(x+y)+z равносильно x+(y+z)
x+x равносильно x
x*x равносильно x
x+(x*y) равносильно x
Основные тождества алгебры логики.
Формулы
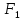 и
и
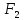 называются тождественными или
эквивалентными, если соответствующие
им функции
называются тождественными или
эквивалентными, если соответствующие
им функции
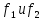 равны, т.е.
равны, т.е.
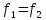 .
Тогда запись
.
Тогда запись
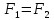 означает, что
означает, что
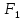 и
и
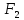 тождественны.
тождественны.
Пример:
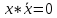
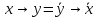 и т.д.
и т.д.
Определение.
Две
формулы
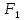 и
и
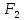 называются эквивалентными, если они
задают одну и ту же булеву функцию от
всех переменных, входящих в эти формулы.
называются эквивалентными, если они
задают одну и ту же булеву функцию от
всех переменных, входящих в эти формулы.
Используя
основные положения алгебры логики,
нетрудно убедится в справедливости
следующих восьми аксиом. Пусть х –
некоторая логическая переменная. Тогда
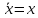
-
х=х, что означает возможность исключения из логического выражения всех членов, имеющих двойное отрицание, заменив их исходной величиной;
-
х+х=х; хх=х – правила подобных преоразований, которые позволяют сокращать длину логических выражений;
-
х+0=х;
-
х+1=1;
-
х*0=0;
-
х*1=х;
-
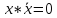 ;
; -
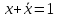 .
.
Таблица основных тождеств алгебры логики.
|
1 |
а) б)
|
Переместительный (коммутативный) закон |
|
2 |
а)
б)
|
Распределительный закон: Конъюнкция относительно дизъюнкции Дизъюнкция относительно конъюнкции |
|
3 |
а)
б)
|
Сочетательные законы (ассоциативные) |
|
4 |
а)
б) х+х=х |
Закон повторения (тавтологии) |
|
5 |
а)
б)
|
Закон поглощения |
|
6 |
|
Закон дополнительности |
|
7 |
а)
б)
|
Правила де Моргана |
|
8 |
|
Закон двойного отрацания |
|
9 |
а)
б)
( |
Закон склеивания |
|
10 |
а) х*1=х б) х+1=1 |
Закон универсального множества |
|
11 |
а) х*0=0 б) х+0=х |
Закон нулевого множества |
Дистрибутивные законы. (б) не имеет аналога в обычной алгебре
Законы Отрицания
«Правила» из основных тождеств
-
Если в логическом произведении один из множителей равен нулю, то и логическое произведение равно нулю.
-
Если в логическом произведении, содержащем не менее двух множителей, имеется множитель, равный единице, то этот множитель можно удалить.
-
Если в логической сумме, содержащей не менее двух слагаемых, имеется слагаемое, равное нулю, то это слагаемое можно удалить.
-
Если в логической сумме одно из слагаемых равно единице, то логическая сумма равна единице.
Если F’ – подформула формулы F, и если заменить любое из её вхождений на любую эквивалентную формулу B’, то формула F перейдёт в формулу В, которая будет эквивалентна F.
Это
утверждение вместе с тождествами для
элементарных функций, к которым
присоединяются все тождества, получаемы
подстановкой вместо переменных
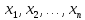 любых форм, позволяет осуществлять
эквивалентные преобразования и, тем
самым, получать новые тождества.
любых форм, позволяет осуществлять
эквивалентные преобразования и, тем
самым, получать новые тождества.
Примеры преобразований
Не сложно установить правильность соотношений, известных как законы де Моргана:
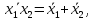
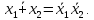
Из законов де Моргана вытекают следствия
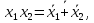
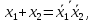
с помощью которых появляется возможность выражать конъюнкцию через дизъюнкцию и отрицание или дизъюнкцию через конъюнкцию и отрицание.
Законы де Моргана и следствия из них справедливы для любого количества переменных:
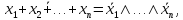
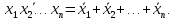
Для логических функций устанавливаются соотношения, известные как законы поглощения:
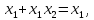
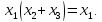
Функция сложения по модулю 2 – функция, выражаемая следующим образом:
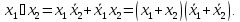
Функция сложения по модулю 2 обладает следующими свойствами: коммутативности (переместительный закон):
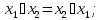
ассоциативности (сочетательный закон):
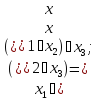
дистрибутивности (распределительный закон):
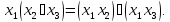
Принципы двойственности.
Определение.
Функция
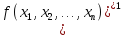 равная функции
равная функции
 называется двойственной функцией к
функции
называется двойственной функцией к
функции
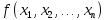 .
.
Таблица
для двойственной функции получается
из таблицы для функции
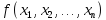 инвертированием (т.е. заменой 0 на 1 и 1
на 0) значений функции и заменой порядка
следования инвертированных значений
функции на противоположный
инвертированием (т.е. заменой 0 на 1 и 1
на 0) значений функции и заменой порядка
следования инвертированных значений
функции на противоположный
функция 0 двойственна 1
функция 1 двойственна 0
функция
х двойственна
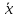
функция
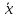 двойственна х
двойственна х
функция
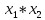 двойственна
двойственна
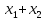
функция
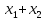 двойственна
двойственна
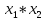
Из определения двойственности вытекает, что:
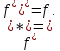
Для
получения формулы
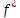 ,
двойственной к формуле
,
двойственной к формуле
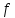 ,
необходимо в формуле
,
необходимо в формуле
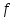 всюду заменить 0 на 1, а 1 на 0 (& на +, а +
на &).
всюду заменить 0 на 1, а 1 на 0 (& на +, а +
на &).
Или
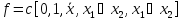
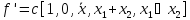
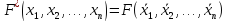 ,
двойственная формула выражается как
отрицание формулы, полученной из исходной
замещением каждой переменной её
отрицанием. Таблица соответствия
двойственной функции получается заменой
значений аргументов в исходной функции
на противоположные, т.е. 0 заменяется на
1, а 1 на 0.
,
двойственная формула выражается как
отрицание формулы, полученной из исходной
замещением каждой переменной её
отрицанием. Таблица соответствия
двойственной функции получается заменой
значений аргументов в исходной функции
на противоположные, т.е. 0 заменяется на
1, а 1 на 0.
Функция, равносильная своей двойственной, называется самодвойственной.
Если
формулы
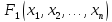 и
и
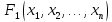 равносильны, то и двойственные им формулы
равносильны, то и двойственные им формулы
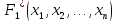 и
и
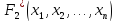 также равносильны.
также равносильны.
Краткое содержание лекции.
Тождества алгебры логики являются важной составной частью алгебры логики, позволяют выполнять эквивалентные преобразования и получать новые уравнения и тождества.

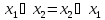 или
или
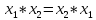
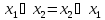 или
или