Лекции 15-16

Тема: Фракталы.

Содержание:

1. Введение. Краткая историческая справка о фракталах.

2. Фракталы – элементы геометрии в природе.

3. Объекты, обладающие фрактальными свойствами, в природе.

4. Определение терминологии «фракталы».

5. Классы фракталов.

6. Описание фрактальных процессов.

7. Процедуры получения фрактальных множеств.

8.1 Ломаная Коха (процедура получения).

8.2 Снежинка Коха (Фрактал Коха).

3. Губки Менгера.

9. Примеры применения фракталов.

Введение. Краткая историческая справка о фракталах.

Данная лекция посвящена обсуждению фрактальных множеств, или просто фракталов. Такие множества известны сто лет и появлялись в разных областях науки. Но только недавно (более 30 лет тому назад) они стали предметом математического исследования.

В основе этого явления лежит простая идея: бесконечное по красоте и разнообразию множество фигур можно получить из относительно простых конструкций при помощи всего двух операций — копирования и масштабирования

На рубеже XIX и XX веков изучение фракталов носило скорее эпизодический, нежели систематический характер, потому что раньше математики в основном изучали «хорошие» объекты, которые поддавались исследованию при помощи общих методов и теорий.. В 1872 году немецкий математик Карл Вейерштрасс построил пример непрерывной функции, которая нигде не дифференцируема. Однако его построение было целиком абстрактно и трудно для восприятия. Поэтому в 1904 году швед Хельге фон Кох придумал непрерывную кривую, которая нигде не имеет касательной, причём её довольно просто нарисовать. Один из вариантов этой кривой носит название «снежинка Коха».

В 1918 году вышел почти двухсотстраничный труд Жюлиа, посвященный итерациям комплексных рациональных функций, в котором описаны множества Жюлиа – целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно. Несмотря на то что это работа прославила Жюлиа среди математиков того времени, о ней довольно быстро забыли.

Идеи самоподобия фигур подхватил француз Поль Пьер Леви, будущий наставник Бенуа Мандельброта. В 1938 году вышла его статья «Плоские и пространственные кривые и поверхности, состоящие из частей, подобных целому», в которой описан ещё один фрактал – С-кривая Леви.

Вновь внимание к работам Жюлиа и Леви обратилось лишь полвека спустя, с появлением компьютеров: именно они сделали видимыми богатство и красоту мира фракталов. Ведь никто не мог посмотреть на изображения, которые мы сейчас знаем как изображения множества Мандельброта, нагому что необходимое количество вычислений невозможно провести вручную. Первым, кто использовал для этого компьютер был Бенуа Мандельброт.

В 1982 году вышла книга французско-американского математика еврейского происхождения Бенуа Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал практически всю имевшуюся на тот момент информацию о фракталах и в легкой и доступной манере изложил её. Основной упор в своем изложении Мандельброт сделал не на тяжеловесные формулы и математические конструкции, а на геометрическую интуицию читателей. Благодаря иллюстрациям, полученным при помощи компьютера, и историческим байкам, которыми автор умело разбавил научную составляющую монографии, книга стала бестселлером, а фракталы стали известны широкой публике. Их успех среди нематематиков во многом обусловлен тем, что с помощью весьма простых конструкций и формул, которые способен понять и старшеклассник, получаются удивительные по сложности и красоте изображения. Когда персональные компьютеры стали достаточно мощными то появилось даже целое направление в искусстве — фрактальная живопись, причем заниматься ею мог практически любой владелец компьютера. Сейчас в интернете можно легко найти множество сайтов, посвященных этой теме.

После 1982 серьезные работы, обзоры, популярные статьи и книги о фракталах стали появляться десятками, если не сотнями. С 1993 года в издательстве World Scientific выходи г специальный периодический журнал «Фракталы». Так нужно ли знакомить будущих аналитиков с фракталами? Думаю, что да.

Несмотря на обширную литературу, многие люди, включая студентов, аспирантов и значительную часть работающих математиков, имеют довольно смутное представление о фракталах. Во-вторых, во многих популярных книгах читатель видит массу цветных картинок и любопытных примеров, но не найдет ни точных определений, ни строго доказанных результатов. С другой стороны, работы профессиональных математиков, как правило, слишком трудны для начинающих. Они обычно посвящены довольно специальным вопросам и часто предполагают заранее известными все связи и мотивировки.

Последняя и, может быть, самая важная причина состоит в том, что изучение в вузе геометрии, анализа и арифметики фракталов, является одним из лучших способов, для молодого математика-аналитика активно и прочно овладеть основными ­математическими знаниями.

Когда-то большинству людей казалось, что геометрия в природе ограничивается такими простыми фигурами, как линия, круг, коническое сечение, многоугольник, сфера, квадратичная поверхность, а также их комбинациями. К примеру, что может быть красивее утверждения о том, что планеты в нашей солнечной системы движутся вокруг солнца по эллиптическим орбитам?

Однако многие природные системы настолько сложны и нерегулярны, что использование только знакомых объектов классической геометрии для их моделирования представляется безнадежным. Как к примеру, построить модель горного хребта или кроны дерева в терминах геометрии? Как описать многообразие биологических конфигураций, которые мы наблюдаем в мире растений и животных? Представьте себе всю сложность системы кровообращения, состоящей из множества капилляров и сосудов и доставляющей кровь к каждой клеточке человеческого тела. Представьте, как хитроумно устроены лёгкие и почки, напоминающие по структуре деревья с ветвистой кроной.

Столь же сложной и нерегулярной может быть и динамика реальных природных систем и явлений. Как подступиться к моделированию каскадных водопадов или турбулентных процессов, определяющих погоду?

Фракталы - подходящие средства для исследования поставленных вопросов. Термин фрактал относится к некоторой статичной геометрической конфигурации, такой как мгновенный снимок водопада. Нередко то, что мы наблюдаем в природе, интригует нас бесконечным повторение одного и того же узора, увеличенного или уменьшенного во сколько угодно раз. Например, у дерева есть ветви. На них ветвях есть ветки поменьше и т.д. Теоретически, элемент «разветвление» повторяется бесконечно много paз становясь все меньше и меньше. То же самое можно заметить, разглядывая фотографию горного рельефа. Попробуйте немного приблизить изображение горной гряды - вы снова увидите горы. Так проявляется характерное для фракталов свойство самоподобия.

Существуют фигуры, описать которые невозможно с помощью векторной и растровой графики Примером являются лист папоротника, облака, морозные узоры, береговая линия, клякса. Если увеличивать изображения, выполненные в растровой или векторной графике, то постепенно получим прямую линию или точку. Увеличивая же фигуры и узоры, мы увидим, что они повторяются. Такие графические изображения можно представить с помощью фрактальной графики. В отличие от растровой и векторной графики – фрактальная графика основана на чистом программировании. Причем изображения строятся на основе рекурсии, то есть на способности функции обращаться к самой себе или к другим функциям, в которых есть обращение к такой функции,

Фрактал – объект довольно сложной формы, получающийся в результате выполнения простого и итерационного цикла. Итерационность, рекурсивность обуславливают такие свойства фракталов, как самоподобие отдельные части похожи по форме на вест фрактал в целом.

Природные объекты, обладающие фрактальными свойствами

В живой природе:

• Кораллы

• Морские звезды и ежи

• Морские раковины

• Цветы и растения (брокколи, капуста)

• Плоды (ананас)

• Кроны деревьев и листья растений

• Кровеносная система и бронхи людей и животных

В неживой природе:

• Границы географических объектов (стран, областей, городов)

• Береговые линии

• Горные хребты

• Снежинки

• Облака

• Молнии

• Образующиеся на стеклах узоры

• Кристаллы

• Сталактиты, сталагмиты, геликтиты.

Определение терминологии «фрактала»

Фракталы! У этого понятия нет строгого определения. Поэтому слово «фрактал» не является математическим термином. Обычно так называют геометрическую фигуру, которая удовлетворяет одному или нескольким из следующих свойств:

• Обладает сложной нетривиальной структурой при любом увеличении (на всех масштабах). В этом отличие от регулярных фигур (таких как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, то он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, то есть на всех шкалах мы увидим одинаково сложную картину.

• Является (приближённо) самоподобной.

• Обладает дробной хаусдорфовой (фрактальной) размерностью или превосходящей топологическую.

• Может быть построена рекурсивными процедурами.

В работах по фракталам самоподобие используется в качестве определяющего свойства. Следуя Бенуа Мадельброту, мы принимаем точку зрения, согласно которой фракталы должны определяться в терминах фрактальной (дробной) размерности. Отсюда и происхождение слова фрактал (от лат. fractus - дробный).

Понятие дробной размерности представляет собой сложную концепцию, которая излагается в несколько этапов. Прямая - это одномерный объект, а плоскость - двумерный. Если хорошенько перекрутив прямую и плоскость, можно повысить размерность полученной конфигурации; при этом новая размерность обычно будет дробной в некотором смысле, который нам предстоит уточнить. Связь дробной размерности и самоподобия состоит в том, что с помощью самоподобия можно сконструировать множество дробной размерности наиболее простым образом. Даже в случае гораздо более сложных фракталов, таких как граница множества Мандельброта, когда чистое самоподобие отсутствует, имеется почти полное повторение базовой формы во все более и более уменьшенном виде.

Многие замечательные свойства фракталов открываются при изучении итерированных отображений. При этом начинают с некоторой функции 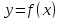и рассматривают поведение последовательности 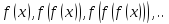. В комплексной плоскости работы такого рода восходят, по всей видимости, к имени Кэли, который ещё в 1979 г. исследовал метод Ньютона нахождения корня в приложении к комплексным, а не только к вещественным, функциям. Замечательного прогресса в изучении итерированных комплексных отображений добились Гастон Жюлиа и Пьер Фату (1919). Естественно, все было сделано без помощи компьютерной графики. В наши дни. многие уже видели красочные постеры с изображением множеств Жюлиа и множества Мандельброта, тесно с ними связанного.

Изучение фракталов открывает замечательные возможности, как в исследовании бесконечного числа приложений, так и в области чистой математики. Но в то же время, как это часто случается в так называемой новой математике, открытия опираются на пионерские работы великих математиков прошлого. Исаак Ньютон понимал это, говоря «Если я видел дальше других, то только потому, что стоял на плечах гигантов».