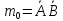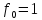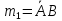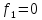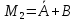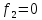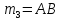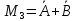Дискретная Математика / Lektsia_12
.docxЛекция №12
Тема: Канонические формы переключательных функций. Нормальные и совершенные нормальные конъюнктивные формы переключательных функций.
Содержание
-
Нормальные и совершенные нормальные конъюнктивные формы переключательных функций.
-
Свойства СКНФ.
-
Свойства совершенных форм СДНФ и СКНФ.
-
Переход от табличного представления переключательных функций к алгебраическому
-
для СДНФ
-
для СКНФ
Нормальные и совершенные нормальные конъюнктивные формы переключательных функций
Определение. Логическая сумма любого количества различных независимых переменных, входящих с отрицанием или без него, называется элементарной дизъюнкцией.

По
аналогии с предыдущим пунктом
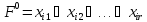 - элементарная дизъюнкция, r
- ранг элементарной дизъюнкции.
- элементарная дизъюнкция, r
- ранг элементарной дизъюнкции.
Если функция задана формулой в виде конъюнкции элементарных дизъюнкций, то, следовательно, функция представлена конъюнктивно нормальной формой (КНФ):
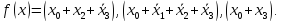
Любая переключательная функция может быть задана и своей совершенной конъюнктивной нормальной формой (СКНФ). Для этого используется конституенты нуля - макстермы.
Конституентой
нуля (макстермом) называют переключательную
функцию n
аргументов, которая принимает значение,
равное 0 только на одном наборе. Имеется
2n
конституент нуля. Согласно таблицы,
конституентами нуля являются
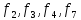 .
.
Совершенной конъюнктивной нормальной формой (СКНФ) переключательной функции называется конъюнкция тех конституент нуля, которые обращаются в нуль на тех же кортежах (наборах) значений аргументов, что и данная функция.
Свойства СКНФ
Совершенная КНФ удовлетворяет следующим условиям:
-
в ней нет двух одинаковых множителей;
-
ни один из множителей не содержит двух одинаковых слагаемых;
-
ни один множитель не содержит каких-нибудь переменную вместе с ее отрицанием;
-
каждый множитель содержит в качестве слагаемого
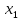 или
или
 для любого i=1,
2, ...,n
для любого i=1,
2, ...,n
Свойства совершенных форм СКНФ и СДНФ
-
Однозначное представление функции. Дают только совершенные нормальные формы (СДНФ и СКНФ).
-
В СДНФ (СКНФ) нет двух одинаковых минтермов (макстермов).
-
В СДНФ (СКНФ) ни один минтерм (макстерм) не содержит двух одинаковых множителей (переменных).
-
В СДНФ (СКНФ) ни один минтерм (макстерм) не содержит вместе с переменной и ее отрицание.
Любая функция алгебры логики, кроме абсолютно истинной и абсолютно ложной функции, может быть представлена в совершенной (СКНФ и СДНФ) форме.

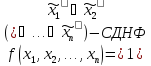
где
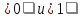 - символы обобщённой конъюнкции и
дизъюнкции конституэнт нуля и единицы
соответственно.
- символы обобщённой конъюнкции и
дизъюнкции конституэнт нуля и единицы
соответственно.
Переход от табличного представления переключательной функции к алгебраическому (для СДНФ).
Минтермы и макстермы используются для перехода от табличного представления функции к алгебраическому.
Пример. Минтермы и макстермы функции даны в таблице.
|
A |
B |
Минтермы |
Макстермы |
Значения функции F(A,B) |
|
0 |
0 |
|
|
|
|
0 |
1 |
|
|
|
|
1 |
0 |
|
|
|
|
1 |
1 |
по «1» |
по «0» |
|
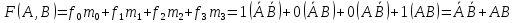
В общем случае алгебраическое выражение любой логической функции представлено в следующей форме:
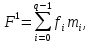
где
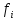 – значение функции (0 или1), а
– значение функции (0 или1), а
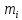 – минтерм, соответствующие i-тому
кортежу переменных. Это совершенная
дизъюнктивная нармальная форма (СДНФ).
– минтерм, соответствующие i-тому
кортежу переменных. Это совершенная
дизъюнктивная нармальная форма (СДНФ).
Переход от табличного представления переключательной функции к алгебраическому (для СКНФ).
Алгебраическое выражение функции (для СКНФ) получается в виде произведения:

где
 и
и
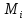 – значение функции и макстерм,
соответствующие i-тому
набору переменных.
– значение функции и макстерм,
соответствующие i-тому
набору переменных.
Получаем СКНФ в виде:
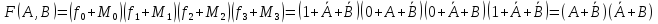
Если
в выражениях
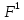 и
и
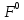 вместо
вместо
 использовать
использовать
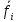 инверсии значения функции, то получается
СДНФ и СКНФ для функции, являющейся
инверсией заданной.
инверсии значения функции, то получается
СДНФ и СКНФ для функции, являющейся
инверсией заданной.

Так осуществляется переход от таблицы истинности к алгебраическому представлению логической функции, и любая логическая функция может быть представлена в виде СДНФ и СКНФ.
Краткое основное содержание лекции
-
Любая переключательная функция ПФ (отличная от константы 1) имеет одну СКНФ и несколько КНФ.
-
Любая КНФ получается в результате сокращения СКНФ.
-
От любой КНФ можно перейти к СКНФ (это развёртывание).
-
Любому табличному представлению функции соответствует алгебраическое.