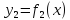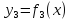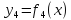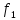Дискретная Математика / Lektsia_5_Matematicheskaya_logika

Лекция №5

Тема: Математическая логика. Булевы функции.

Содержание

1. Математическая логика. Краткий исторический экскурс.

2. Булевы функции. Основные правила и определения.

3. Способы задания булевых функций.

4. Булевы функции одной переменной.

5. Область определения булевых функций.

6. Элементарные функции алгебры логики.

Основатель математической логики ирландский математик Джордж Буль – отец Этель Лилиан Войнич – автор книги «Овод» (1815-1864). В книгах «математический анализ логики» (1847) и «Законы мышления» (1854) Буль изложил «алгебру логики» - алгебру Буля. В алгебре Буля буквы обозначают высказывания, а все правила обычной алгебры остаются в силе. Новая алгебра является логикой и получила название алгебры логики. Буль разработал алфавит, орфографию и грамматику.

В алгебре логики высказывания рассматриваются не по их содержанию или смысл, а только в отношении того, истинны они или ложны. Каждое высказывание может быть только истинно или ложно. Истинность высказывания обозначают «1», а ложность – «0».

За 150 лет до этого немецкий математик Лейбниц (1646 – 1716) предсказал появление математической логики. Предложил в логике использовать математическую символику и высказал возможностьприменения двоичной системы счисления «логика обретает символьный язык, конкретность законов, распространяется за рамки гуманитарных наук».

Булевы функции. Основные понятия и определения.

Булевы функции относятся к классу двузначных однородных функций, которые используются для описания конечных автоматов, ЭВМ и ВС. Булеву алгебру образуют множества всех булевых функций вместе с операциями отрицания, конъюнкции, дизъюнкции, импликации и т.п.

Основным понятием алгебры логики является высказывание. Высказывание - это некоторое утверждение, о котором можно ска­зать, что оно истинно или ложно. Например, «Херсон - город на Днепре», «солнце всходит утром» - истинные высказывания, а «на улице идет дождь» - может быть истинным или ложным в зависимости от дополнительных сведе­ний. Любое высказывание можно обозначить символом х и считать, что х=1 при истинности, а х=0 при ложности высказывания.

Рассматриваем функцию f(x₁,x₂,…,x_n), аргументы которых опре­делены на множестве Е₂₌{0,1} и таковы, что f(x₁,x₂,…,x_n)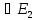 когда 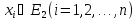. Эти функции будем называть функциями алгебры логики или булевыми функциями. Логическими (булевыми) переменными в булевой алгебре называют ве­личины, которые независимо от их конкретной сущности могут принимать лишь два значения («нуль» (0) и «единица» (1))..Если переменная х имеет единичное значение, мы запи­сываем х=1, если нулевое - х=0. Булевой или переключательной функцией f(x₁,x₂,…,x_n-1), называют функцию, которая как и ее n аргументов может при­нимать лишь два значения - 0 или 1.

Совокупность значений аргументов является кортежем, точкой или набором. Функция, зависящая от n аргумеентов, называется n-местной и является полностью определенной, если указаны ее значения для всех наборов(кортежей, точек) значений аргументов. Каждому i-ому кортежу можно поставить в соответствии «терм» - произвольное элементарное произведение двоичных переменных. «Терм» 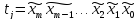. Если в i-том кортеже x_j=1, то в терме вместо 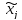стоит переменная, х_j. если хj=0. то -

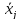
Способы задания булевых функций.

Три способа задания переключательной функции: вербаль­ный (или словесный), аналитический и табличный. Аналитическое задание функции - описание ее аналитическим выражением (формулой). Например:

f(х,х₂х₃) = x₁х₂ + х₂(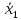 +х₁);f₂(аbс) = аbс + аbс . Одним из распро­страненных способов задания булевой функции, является ««»задание с помо­щью таблицы соответствия(истинности). В колон­ках 1,2, 3 даны вое возможные кортежи значений 3-х аргументов, т.е. сочета­ние нулевых и единичных значений 3-х аргументов. В колонке 4 - значение функций.

X2	X1	X0	f(x2,x1,x0) кортеж (набор, точка)
1	2	3	4
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	0

Любое целое неотрицательное число N можно рассматривать в виде суммы:

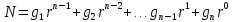
где г - основание системы счисления;

g — множитель, который принимает значения от 0 до (r-1).

Количество слагаемых определяется разрядностью чисел.

Кортеж значений аргументов можно рассматривать как запись целого положительного числа в двоичной системе счисления (r=2), тогда х₀ - разряд единиц, x₁ - разряд двоек, х₂ - разряд четверок. Например, шестой набор 1*2² +0*2^2,+1*2⁰. Первый набор называется нулевой, последний - единичный.

Булевы функции одной переменной.

Таблица соответствия для булевых функций одной переменной имеет вид:

x
0	1	0	1	0
1	1	0	0	1

Функци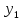и и 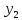представляют собой функции-константы:

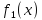– является абсолютно истинной (константа единицы);

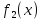– абсолютно ложная (константа нуля);

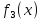– логическое отрицание или НЕ, инверсия х (читается как «не х», изображается как ), это единственная нетривиальная функция;

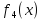– переменная х ( повторяет значение переменной х, и просто совпадает с ней).

Область определения булевой функции

Областью определения булевой (переключательной) функции (ПФ) n аргументов является совокупность 2ⁿ булевых кортежей.

Булевая функция от двух элементов является полностью определённой если указаны её значения для каждого из четырёх возможных наборов (2²=4), функция трёх аргументов – на 8 (2³=8) наборах.

Булева функция n аргументов является полностью определённой, если заданы все её значения для каждого из 2ⁿ наборов.

Число всех функций, зависящих от переменных х₁,х₂,…,х_n равно .

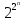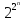Действительно. Переключательная функция (ПФ) n аргументов определена на 2ⁿ наборах, на которых она может принимать «0» или «1» из общего количества 2ⁿ. В соответствие каждой переключательной функции можно поставить 2ⁿ - разрядное двоичное число. Но колическтво различных 2ⁿ-разрядных чисел равно , а следовательно и количество различных переключательных чисел равно

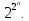
От двух аргументов существует 16 булевых функций, от трёх – 256, от 4 – 65500 функций.

Из функций двух переменных строится любая переключательная функция.

Элементарные функции алгебры логики

В математической логике употребляются элементарные функции, которые играют такую же важную роль, как, например, хⁿ или sin x в математическом анализе.

Примеры элементарных функций одной переменной:

– константа «0»;

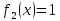– константа «1»;

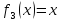–тождественная функция;

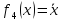– отрицание х («не х»).

Табличное представление этих функций:

х
0	0	1	0	1
1	0	1	1	0

Основное содержание лекции

1. Булевы функции – это двухзначные однородные функции, используемые для описания ЭВМ и систем.

2. Булева алгебра – множество всех булевых функций вместе с операциями отрицания, дизъюнкции, конъюнкции, импликации и т.п.

3. Используется три способа задания Булевых функций.

4. Булева (переключательная) функция определена на 2ⁿ наборах. Принимает только два значения: 0 или 1.