Диаграмма Карно-Вейча для 7-и переменных

Контрольные вопросы

1. Изобразите карты Карно для 2-7 переменных.

2. В чем преимущество этого метода перед другими, ранее изученными?

3. Назовите правила минимизации метода Карно-Вейча.

Методические указания

Метод получения минимальных форм с помощью карт Карно объясняется на примерах.

Пример 1:Найти минимальные ДНФ и КНФ функции f(a,b,c) методом Карно-Вейча.

f(a,b,c)=abcabcabcabcabc

Объединить единицы можно двумя способами:

а)

	b		b
a	1	1	1	0
a	0	0	1	1
	c	c		c

б)

	b		b
a	1	1	1	0
a	0	0	1	1
	c	c		c

Этим вариантам соответствуют две минимальных ДНФ:

а) f(a,b,c,d)=abacab;

б) f(a,b,c,d)=abbc ab.

Для получения минимальной КНФ следует объединить нули функции:

	b		b
a	1	1	1	0
a	0	0	1	1
	c	c		c

f(a,b,c)=(a b)( abc)

Пример 2: Найти минимальную ДНФ булевой функции:

f(a,b,c,d)=abcdabcdadcdabcdabcdabcdabcd.

Карта Карно для этой функции приведена ниже. На ней показан способ наиболее рационального покрытия единиц.

	b		b
a	1	0	0	0	c
	1	0	0	1	c
a	1	0	1	1
	0	1	0	0	c
	d	d		d

Минимальная ДНФ этой функции будет иметь вид:

f(a,b,c,d)=cdabd abcabcd.

Индивидуальные задания

8.1 С помощью карт Карно найдите МДНФ и МКНФ булевой функции:

1. f(a,b,c,d)=ab  (cd a

2. f(a,b,c,d)=dcbac

3. f(a,b,c,d)=adc a b

4. f(a,b,c,d)=dba c ab

5. f(a,b,c,d)=bac d

6. f(a,b,c,d)=ad bac

7. f(a,b,c,d)=dbadcb

8. f(a,b,c,d)=acbdba

9. f(a,b,c,d)=bdcada

10. f(a,b,c,d)=bcdabc

11. f(a,b,c,d)=bcadbd

12. f(a,b,c,d)=cbadcb

13. f(a,b,c,d)=dbca

14. f(a,b,c,d)=dcdba

15. f(a,b,c,d)=dbaca

16. f(a,b,c,d)=dbdbac

17. f(a,b,c,d)=cbdbdac

18. f(a,b,c,d)=cbdab

19. f(a,b,c,d)=adaddcb

20. f(a,b,c,d)=ccaddcb;

21. f(a,b,c,d)=acbdba

22. f(a,b,c,d)=bdcada

23. f(a,b,c,d)=bcdabc

24. f(a,b,c,d)=bcadbd

25. f(a,b,c,d)=cbadcb

26. f(a,b,c,d)=dbadcb

27. f(a,b,c,d)=acbdba

28. f(a,b,c,d)=bdcada

29. f(a,b,c,d)=bcdabc

30. f(a,b,c,d)=bcadbd.

Практическое занятие №14 Тема: Геометрический метод нахождения минимальной днф и кнф.

Цель работы: овладение минимизацией булевых функций методом Блейка-Порецкого и геометрическим методом.

Теоретическая часть Геометрическое представление функций алгебры логики

Многие преобразования, выполняемые над булевыми функциями, удобно интерпретируются с геометрическим представлением функций. Функцию двух переменных можно интерпретировать как некоторую плоскость, заданную в системе координат X₁X₂.

На каждой оси откладываются единичные отрезки X₁X₂ и получаем квадрат, вершины которого соответствуют комбинациям переменных. Это и будет геометрическое представление функций 2-х переменных (рис.1).

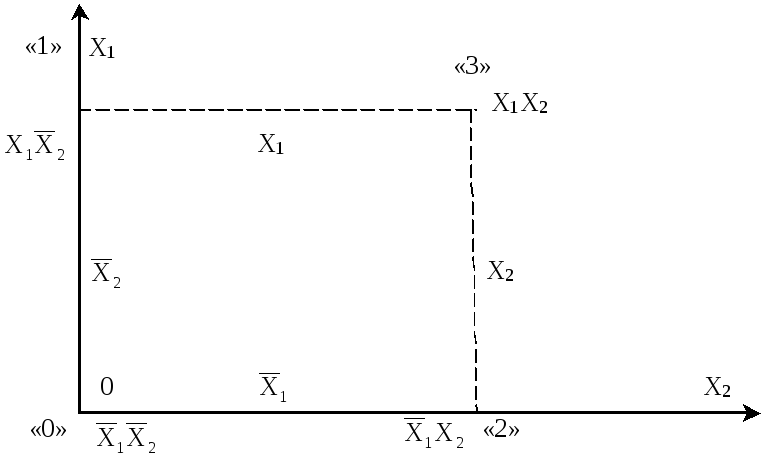
Рис.1.

Из такого геометрического представления функций двух переменных следует: две вершины, принадлежащие одному и тому же ребру, называются соседними и они «склеиваются» по переменной, меняющейся вдоль этого ребра

.

Для функций 3-х переменных геометрическое представление интерпретируется в виде куба (рис.2.), вершины которого обозначают десятичными цифрами, двоичными цифрами и переменными Х. Ребра куба поглощают вершины, грани поглощают свои ребра и, следовательно, вершины.

В общем случае совокупность векторов отображается на множество вершин n-мерного куба. Все такие вершины образуют логическое пространство.

Булева функция отображается на n-мерном кубе путем выделения вершин, соответствующих векторам, на которых функцияпринимает значения «1». Такие значения отмечаются точками.

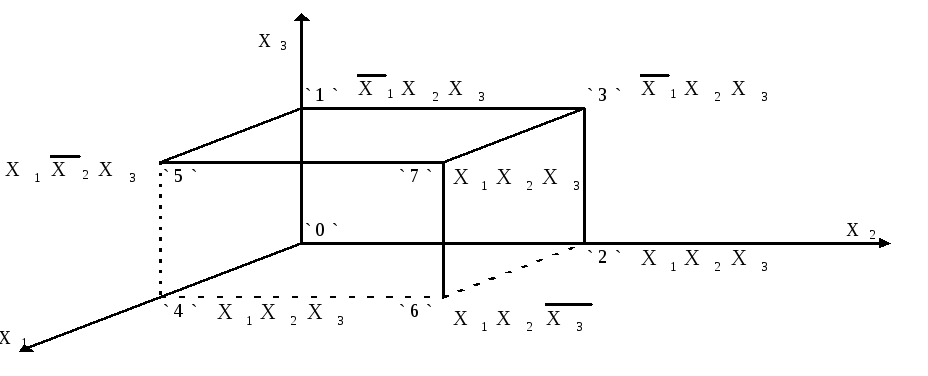
Рис.2.

В геометрическом смысле каждый набор , т.е. каждая вершина, может рассматриваться как n-мерный вектор, определяющий точку n-мерного пространства. Поэтому все множество наборов, на которых определена функция n переменных, представляется в виде вершин n-мерного куба.

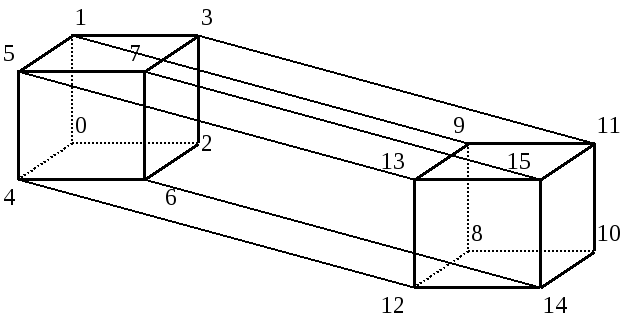
Рис.3.

Координаты вершин куба должны быть указаны в порядке, соответствующему порядку перечисления переменных в записи функций. Геометрическое представление может использоваться при разработке методов минимизации с применением минимизирующих карт.

Функция 4-х переменных геометрически представляется в виде 4-мерного куба (рис.3).

Функция 5-ти переменных представляется в виде 5-мерного куба (рис 4).и т.д

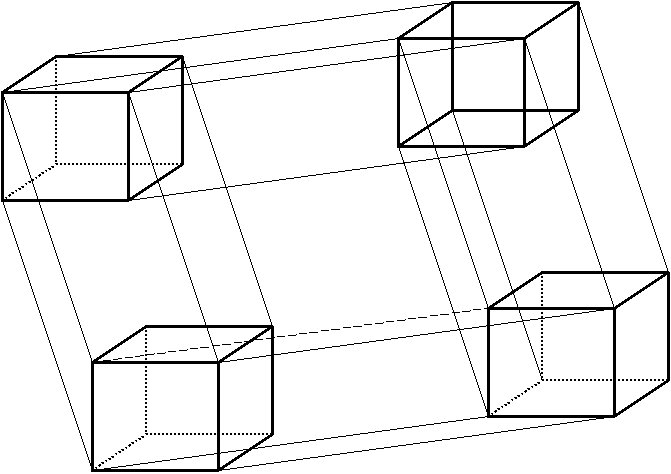
Рис. 4

Формулировка геометрической задачи (задачи о покрытии):необходимо найти для данного множества N такое покрытие гранями, принадлежащими N_f,

, чтобы ранг был наименьшим.

Эта задача эквивалентна задаче о минимизации булевой функции.

Следовательно, задача минимизации булевых функций имеет две постановки:

• в аналитической форме;

• в геометрической форме (задача о покрытии).

Употребляются два языка: аналитический и геометрический.