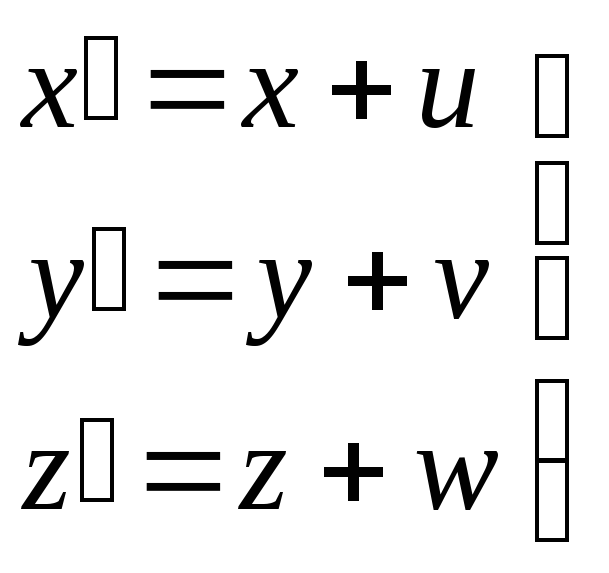Херсонський національний технічний університет Кафедра загальної та прикладної фізики

МЕХАНІКА СУЦІЛЬНИХ СЕРЕДОВИЩ Лекція 1.9.

	1.9. МЕХАНІКА СУЦІЛЬНИХ СЕРЕДОВИЩ
	НАПРУЖЕНИЙ СТАН ТВЕРДИХ ТІЛ. ПОНЯТТЯ ДЕФОРМАЦІЇ ТА ЇЇ ОСНОВНІ ТИПИ
	ЗАКОН ГУКА ДЛЯ ДЕФОРМАЦІЙ РОЗТЯГУВАННЯ ТА ЗСУВУ. МОДУЛЬ ЮНГА ТА МОДУЛЬ ЗСУВУ
	РІВНЯННЯ РУХУ ІДЕАЛЬНОЇ РІДИНИ
РІВНЯННЯ БЕРНУЛЛІ

• Напружений стан твердих тіл. Поняття деформації та її основні типи

Механічні властивості твердих тіл (ТТ) віддзеркалюють його реакцію на дію зовнішніх сил. Ці властивості визначаються щонайперше силами зв’язку поміж структурними одиницями ТТ. Якщо ТТ має хоча б одну фіксовану в просторі точку і знаходиться під дією зовнішніх сил, то в кожній його точці виникають механічні напруження. Тоді стверджують, що тіло перебуває у напруженому стані.

Якщо в такому тілі виокремити малий елемент об’єму (Мал.1.9.1), то на цей елемент діє два типи сил: об’ємні сили (сила тяжіння, наприклад), котрі діють на всі елементи тіла, їх величина пропорційна об’єму елемента та поверхневі сили, що діють на поверхні елементу об’єму з боку оточуючих цей елемент частин ТТ.

Ці останні поверхневі сили пропорційні площі поверхні елементу. Тому їх завжди відносять до одиниці поверхні елементу і звуть напруженнями:

(1.9.1)

Під час опису напруженого стану вважатимемо напруження однорідним для всього ТТ, а всі частини ТТ такими, що знаходяться в рівновазі, об’ємні сили та моменти покладатимемо відсутніми. Оберемо довільну точку О в тілі і навколо неї побудуємо безкінечно малий куб. Три осі координат спрямуємо за ребрами куба. Розкладемо вектор напруження, діючого на передній грані куба, на три компоненти: одну нормальну та дві дотичні (як на рисункові). Позначимо черезкомпоненту напруження, діючу уздовж- ої осі координат на грані, яка нормальна до- ої осі (). Тоді на малюнкові відповідно зображені три компоненти: нормальне напруження -, та два тангенціальних (дотичних до грані):.

З умов рівноваги випливає, що напруження, діючі на паралельні одна одній грані є однаковими за величинами, тому достатньо розглянути лише компоненти напружень на трьох взаємно нормальних гранях з шести. З умови однорідності напружень та відсутності моментів сили, можна показати також, що для тангенціальних напружень :.

Компоненти напружень на трьох гранях елементу об’єму рис.1 можна упорядкувати у вигляді квадратної таблиці (тензору другого рангу):

(1.9.2)

де діагональні елементи – це нормальні напруження розтяжіння/стискання, а недіагональні елементи – дотичні, або зсувні напруження.

Загалом симетричний тензор другого рангу має шість незалежних компонент, як це видно з (1.9.2). Стовпчики тензору є компонентами векторів напружень на трьох гранях елементу об’єму, причому перший стовпчик відповідає трьом компонентам, показаним на Мал.1.9.1. Отже, тензор (1.9.2) можна розглядати як сукупність трьох векторів-стовпчиків.

Деформації – це процес зміни відстаней поміж точками ТТ під дією зовнішніх напружень. Найпростіші типи деформацій такі: розтягування, зсув, крутіння та згин. А втім, теорія пружності та опору матеріалів доводять, що дві останні деформації є комбінаціями перших двох деформацій, тому простими деформаціями є лише деформація стискання/розтяжіння та деформація зсуву.

Розглянемо три ортогональні осі координат (на цей раз позначимо їх як ) десь в середині ТТ, що піддається деформації.(Мал.1.9.2)

Припустимо, що точка після деформації лишилася на місті, а точказмістилася на векторв нове положення. Розкладемо вектор зміщенняточки на три компоненти, спрямовані уздовж осей координат. Видно, що:

(1.9.3)

Але також зрозуміло, що кожна компонента вектора зміщення є окремою функцією всіх трьох координат:

(1.9.4)

Іншими словами, вектор зміщення є різним в різних точках деформованого тіла, як і кожна його компонента. Тому для диференціалів функцій (1.9.4) можна записати наступну систему рівнянь:

(1.9.4а)

Де під символом відносної деформації ми розуміємо безрозмірну величину, яка визначається частковою похідною (так, наприклад).

Відносні деформації, таким чином, складають тензор другого рангу, подібний до тензора напружень. Цей тензор також є симетричним, що можна довести, виходячи з умов рівноваги та однорідності. Отже і цей тензор має шість незалежних компонент. Діагональні компоненти тензора деформацій описують деформації розтягування/стискання, тоді як недіагональні – деформації зсуву.

(1.9.5)

Існує угода про позначення компонент тензорів (1.11.2) та (1.11.5) одним індексом замість двох згідно до схеми: і далі. Ця схема легко запам’ятовується якщо зобразити її графічно (Мал.1.9.3). В спрощеній нотації тензор деформації, наприклад виглядає так:

(1.9.6)

Порівнюючи (1.9.5) та (1.9.6) зауважимо, що симетрія тензора яскравіше видна в останньому випадку.

• ЗАКОН ГУКА ДЛЯ ДЕФОРМАЦІЙ РОЗТЯГУВАННЯ ТА ЗСУВУ. МОДУЛЬ ЮНГА ТА МОДУЛЬ ЗСУВУ

Діаграми деформації – найбільш повний спосіб опису пружних властивостей ТТ. Ці діаграми є залежностями поміж механічними напруженнями, що виникають в ТТ під час прикладання до нього зовнішніх сил, та деформаціями, ними викликаними. Такі діаграми не залежать від форми (геометрії) зразку, бо - за визначенням є питомими величинами. На Мал.1.9.4 наведено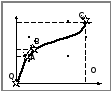типову діаграму деформації для одновісного розтягування циліндричного зразку.

Крива демонструє декілька характерних ососбливостей: при малих напруженнях спостерігається лінійна залежність (ОА). На цій ділянці після зняття напруження деформація зникає під дією внутрішніх сил.Деформація в межах ОА є також оборотною. Проте, це вірно лише для порівняно недовгих за тривалістю напружень. Якщо напруження діє довготривало, виникає явище “кріпа” (повзучості) матеріалу — деформації стають необоротними. Ділянка ОА має назвуобласті пружної деформації (звичайно вона не перевищує типових деформацій ).

За межами пружної області ОА, з виходом за точку А (напруження в цій точці зветься межею пружності - ), крива переходить в так звану пластичну область (ділянка АВ). Величина напруженняв точці В визначає так званумежу течності . Практично межа течності є близькою до межі пружності, як це видно з рис.4. Пластична деформація не зникає повністю після зняття зовнішнього напруження (явище так званої залишкової деформації тіла)

На ділянці ВС тіло деформуєьться („тече”) пластично і необоротно. Точка С (де напруження сягає -межі тривкості) відповідає початку руйнування зразку.

Головні особливості поведінки ТТ в пружній області вивчено ще Робертом Гуком (1678 ). Гук сформулював закон, згідно з яким,