1.6.1 Построение диаграммы приведенного момента сил сопротивления и сил тяжести.

По данным таблицы 1.6. строим график моментов сил полезного сопротивления и тяжести . Для этого строим прямоугольную систему координат. По оси абсцисс откладываем произвольно выбранную длину отрезка 0-12 = 180 мм. Соответствующую одному обороту кривошипа, и разбиваем его на 12 частей.

Масштабный коэффициент по оси абсцисс равен

Масштабный коэффициент по оси ординат:

Значение ординат графика подсчитываем по формуле. Результаты приведены в таблице 1.6.

Из точек 1, 2, 3 и т.д. оси абсцисс откладываем с соблюдением знака ординаты 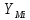которые в масштабе соответствуют значениям приведенных моментов сил. Соединив плавной линией вершины ординатполучим искомую зависимость.

1.7 Построение графиков работ

Методом графического интегрирования диаграммы , получаем диаграмму приведенных работ и диаграмму. Масштаб диаграммы, где Н =80мм– полюсное расстояние диаграммы

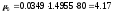
Так как за цикл установившегося движения работа движущих сил по абсолютной величине равна работе сил сопротивления , то ордината графика работ сил сопротивления в конце цикла будет одновременно в том же масштабеизображать работу движущих сил за цикл, но взятую с обратным знаком, так как. Изобразим работу движущих сил с её истинным знаком и покажем зависимость. Для этого отложим ординатувверх от оси абсцисс, предлагая момент движущих сил за цикл, величиной постоянной. Зависимостьвыразится наклонной прямой, соединяющей начало координат с точкой­– концом ординаты в конце цикла.

Теперь строим диаграмму кинетической энергии, откладывая разность ординат диаграмм . Для построения графиканеобходимо из полюса на графике приведенных моментов сил Р провести лучдо пересечения с осью ординат, проведенного параллельно наклонной прямойграфика. Лучотсекает на начальной ординате отрезок. Отрезкибудут одинаковы для всех положений механизма, а потомуотобразится горизонтальной линией.

1.8 Построение графика приведенных моментов инерции звеньев второй группы и приближенного графика кинетической энергии этой группы

Найдем приведенный момент инерций от массы ползунапо формуле 1.4

(1.4)

Результаты вычислений по формуле (1.4) приведены в таблице1.4

Таблица 1.4

№	0, 12	1	2	3	4	5	6	7	8	9	10	11
,	1,92
, мм	0	27.36	52.4	70	68.38	42.63	0	42.63	68.38	70	52.86	27.36
, мм	70
,	0	0.29332	1.07589	1.92	1.8322	0.7121	0	0.71209	1.83216	1.92	1.094862	0.2933
,мм	0	18.3323	67.2431	120	114.51	44.506	0	44.5057	114.51	120	68.42889	18.332

Найдем приведенный Момент инерций от массы ползунапри поступательном движении по формуле 1.5:

(1.5)

Результаты вычислений по формуле (1.5) приведены в таблице 1.5

Таблица 1.5

№	0, 12	1	2	3	4	5	6	7	8	9	10	11
, кг/м2	1,28
, мм	70
, мм	42	48.4	61.05	70	67.09	52.64	42	52.64	67.09	70	61.23	48.4
кг*м2	0.4608	0.6119	0.9736	1.28	1.1758	0.7238	0.4608	0.7238	1.1757	1.28	0.9793	0.6119
, мм	28.8	38.245	60.850	80	73.487	45.24	28.8	45.240	73.486	80	61.210	38.246

Найдем приведенный момент инерций от массы шатунапри вращательном движении по формуле 1.6:

(1.6)

Результаты вычислений по формуле (1.6) приведены в таблице 1.6

Таблица 1.6

№	0,12	1	2	3	4	5	6	7	8	9	10	11
	0,218
,мм	70
ab, мм	70	61.1	35.95	0	35.95	61.1	70	61.1	35.95	0	35.95	61.1
	0.2188	0.1666	0.0577	0	0.0577	0.1667	0.2187	0.1666	0.0576	0	0.0576	0.1667
,мм	13.672	10.416	3.6060	0	3.606	10.416	13.671	10.416	3.6060	0	3.6060	10.416

Определяем общий приведенный момент инерции звеньев II группы по формуле 1.7

(1.7)

Результаты вычислений по формуле (1.7) приведены в таблице 1.7

Таблица 1.7

№	0,12	1	2	3	4	5	6	7	8	9	10	11
	0.218	0.1666	0.0577	0	0.057	0.166	0.2187	0.1666	0.05769	0	0.05769	0.166
кг*м2	0.460	0.6119	0.9736	1.2	1.175	0.723	0.4608	0.7238	1.17578	1.28	0.97936	0.611
,	0	0.2933	1.0758	1.9	1.832	0.712	0	0.7120	1.83216	1.9	1.09486	0.293
	0.6796	1.07191	2.1072	3.2	3.065	1.602	0.6795	1.6026	3.06564	3.2	2.13191	1.071
,мм	42.472	66.9945	131.7	200	191.6	100.16	42.4719	100.162	191.6028	200	133.2449	66.995

По данным таблиц строим графики приведенных моментов инерции отдельных звеньев второй группы

Масштабный коэффициент графиков:

Кривую принимаем как приближенную кривуюизменения кинетических энергий звеньев второй группы и её масштаб определяется по формуле

; ;