2 / ТИПиС / Nechetkie_mnozhestva_MAI

большим значением функции принадлежности тех элементов

,

которые являются одновременно нечеткими прообразами

любых двух

элементов

. Åñëè α

≥0,5, то соответствие

нечетко

нефункционально.

Определение 6. Степень функциональности соответствия

будем назы-

вать величину

β

и определим ее с помощью выра-

жения

β

= − α

.

Åñëè β

≥0,5, то соответствие

нечетко функционально.

Åñëè

α

=

β

=0,5, то соответствие

нечетко функциональ-

но и нечетко нефункционально, т.е. функциональноиндифферентно. Не-

трудно видеть, что в случае, когда соответствие

нечетко функциональ-

но, для любых

справедливо, что

∩

≈ .

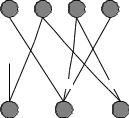
Пример 4. Пусть задано нечеткое соответствие = (X, Y,

),

показанное на рис.9.

Рис.9 Графнечеткогосоответствия.

Äëÿ

каждого

определим

. Получим

=

<

> <

> <

> ,

=

<

> <

>.

<

>

,

=

<

> <

>

Определим α

.

α

=

&

&

&

&

& & & & & &

&

&

=

=

&

&

=

=

.

Отсюда β

=0,1. Соответствие

нечетко нефункционально.

Легко заметить, что если носитель

нечеткого соответ-

ствия

является функциональным соответствием , то величина

α

=0,

β

=1, т.е. соответствие

нечетко функционально.

Определим степень неинъективности и инъективности нечеткого

соответствия. Для четкого соответствия

свойство неинъек-

тивности

можно записать как наличие хотя бы двух таких элементов

, для которых

∩

≠ , а свойство инъективнос-

ти заключается в том, что для любых

справедливо

∩

=

.

Пусть

– произвольное нечеткое соответствие. Опреде-

лим для каждого x X нечеткое множество

:

= < µ

>

, ãäå

<

> ,

поскольку À={x},

=

. Получим семейство нечетких образов

для всех элементов области отправления соответствия .

Определение 7. Степенью неинъективности соответствия

будем на-

зывать величинуα

è

определим

ее с помощью

выражения α

=

µ

& µ

.

Åñëè α

≥0,5, то соответствие

нечетко неинъективно.

Определение 8. Степенью инъективности соответствия

будем назы-

вать величину β

и определим ее с помощью выра-

жения β

=

−α

.

Åñëè β

≥0,5, то соответствие

нечетко инъективно.

Åñëè

α

= β

=0,5, то соответствие

нечетко инъек-

тивно и нечетко неинъективно, т.е. инъективноиндифферентно. В случае,

когда соответствие нечетко инъективно, для любых

справед-

ëèâî, ÷òî

∩

≈ .

Легко заметить, что если носитель

нечеткого соответ-

ствия

является инъенктивным соответствием , то величина

α

=0, β

=1, т.е. соответствие

нечетко инъенктивно.

Определение 9. Степенью всюду определенности соответствия

будем

называть величину

β

и определим ее с помощью

выражения

β

=

&

µ

.

Åñëè

β

≥0,5, то соответствие

нечетко всюду определено.

Åñëè

β

≤0,5, то соответствие

нечетко не всюду определено.

Åñëè

β

=0,5, то соответствие

индифферентно относитель-

но всюду определенности. В случае, когда соответствие

нечетко всюду

определено, для любого

справедливо

.

Если носитель

нечеткого соответствия

ÿâ-

ляется не всюду определенным соответствием, то

β

=0.

β

=

&

µ

.

Åñëè β

≥0,5, то соответствие

нечетко сюръективно. Если

β

≤0,5, то соответствие

нечетко не сюръективно. Если

β

=0,5, то соответствие

сюръективно индифферентно.

В случае, когда соответствие

нечетко сюръективно, для любого

справедливо

.

Если носитель

нечеткого соответствия

ÿâ-

ляется несюръективным соответствием, то

β

=0.

Пример 5. Рассмотрим нечеткое соответствие

, показан-

ное на рис 10. Для каждого

запишем

. Получим

=

<

> <

>

,

=

<

> <

> <

> ,

=

<

> <

> <

> <

> .

Найдем

β

=

& &

=

=

&

&

= .

Следовательно, соответствие

является нечетко всюду определен-

ным. Запишем для каждого

этого же соответствия множества

. Получим

= <

> <

>

<

> ,

=

<

> <

> <

> ,

=

<

> <

> ,

=

<

> .

Находим

β

= & & &

=

=

&

& &

=

. Отсюда следует, что соответствие

ñþðú-

ективно индифферентно.

Определение 10. Степенью нечеткой биективности соответствия бу-

дем называть величину β

и определим ее с помо-

щью выражения

β

= β

& β

& β

.

Åñëè β

≥0,5, то соответствие

нечетко биективно. Если

β

≤0,5,

то соответствие

нечетко небиективно. Если

β

=0,5, то соответствие биективно индифферентно.

3.4. Способы задания нечетких отношений

Определение 11. Нечетким отношением на непроизвольном непустом

множестве Õ называется и через

ϕ

обозначается

Рис. 11 Матрица смежности и граф отношения из примера 6.

Пусть

ϕ

- произвольное нечеткое отношение. Если

< µ

<

>

<

>>

, то выражение

ϕ

представ-

ляет собой нечеткое логическое высказывание , значение истинности ко-

торого равно

µ

<

>

. Отсюда следует, что для задания некоторого

нечеткого отношения

ϕ

íà Õ нечеткую логическую формулу

ϕ

îò

двух переменных или нечеткий предикат, который определен на множе-

ñòâå

Õ2, а значение принимает из интервала

[0;1].

Определение 12. Пусть

ϕ

è

ψ

– некоторые отношения

íà Õ . Степень равенства отношений ϕ ψ обозначает-

ñÿ

µ ϕ ψ

, ãäå

µ ϕ ψ = & µ <

>↔ µ <

> .

<

>

Åñëè

µ ϕ ψ ≥0,5, то отношения ϕ ψ будем называть нечетко

равными и обозначать

ϕ ≈ ψ . Åñëè

µ ϕ ψ

≤0,5 то отношения ϕ ψ

нечетко не равны и обозначать ϕ

ψ

. В случае, когда

µ ϕ ψ

=0,5,

отношения

ϕ ψ

одновременно нечетко равны и нечетко не равны, т.е.

взаимно индифферентны, что обозначается ϕ ψ .

Определение 13. Пусть

ϕ

- некоторое отношение на Õ . Степе-

нью нечеткости отношения называется величина

ρ ϕ

,

ãäå

ρ ϕ

=

− µ ϕ ϕ

, где ϕ − носитель нечеткого отно-

шения

ϕ

.

На основании этого определения можно записать

ρ ϕ

=

−

&

µ

<

>↔ µ

<

> , ãäå

<

>

<

>

<

>=

<

>

Åñëè

µ

<

>=

, òî <

>

, ò.å. µ

<

>= .

Отсюда степень истинности высказывания

µ

<

>↔ µ

<

>

равна 1. Поэтому в формуле

ρ ϕ можно заменить

&

íà

&

. Далее, так как для всех

<

>

<

>

<

>

величина µ

<

>=

, то выражение ρ ϕ

ìîæ-

но записать в виде

ρ ϕ

=

−

&

µ

<

>↔

или, окончательно,

<

>

ρ ϕ

=

−

&

µ

<

> .

<

>

Для любого отношения

можно получить единствен-

ное четкое отношение

ϕ =

ϕ = , нечетко равное или индифферентное

ϕ . Для этого строим график

F*

следующим образом:

= <

>

µ

<

> > .

Для любого четкого отношения ψ =

можно получить бес-

конечно много отношений

ψ

, нечетко равных или индифферентных от-

ношений ψ . Для

получения любого из них достаточно всем парам

<

>

приписать значения функции принадлежности большие

0,5, а всем парам из

– значения меньшие или равные 0,5. Èç

построения нечетких отношений, нечетко равных отношению

ψ =

, и определения нечеткого равенства следует, что все полу-

ченных по ψ

нечеткие отношения будут нечетко равны между собой или

взаимно индифферентны.

Приведем предположения, позволяющие установить нечеткое ра-

венство или неравенство отношений с точностью до взаимной индиффе-

рентности.

Пусть

заданы два

нечетких

отношения

ϕ =

ψ =

. Построим для них четкие отношения

ϕ

=

ψ

=

.

Предположение 1. Если отношения ϕ

=

ψ

=

равны, то нечеткие отношения

нечетко равны

или взаимно индифферентны. ϕ =

ψ =

Предположение 2. Если отношения

ϕ

=

ψ

=

не равны, то нечеткие отношения

ϕ =

ψ =

нечетко не

равны или взаимно индифферентны.

3.5. Операции над нечеткими отношениями

Пусть

ϕ =

ψ =

произвольные нечеткие отноше-

ния на множестве Õ. Будем считать, что отношение

ϕ

нечетко включает-

ся в отношение ψ

, åñëè

. Это обозначается

ϕ

ψ .

Определение 14. Объединением отношений

ϕ èψ

называется нечеткое

отношение

η =

, обозначаемое

η = ϕ ψ

, åñëè

=

. При этом для любых

справед-

ëèâî

<

>=

<

>

<

> .

Определение 15. Пересечением отношений

ϕ

èψ

называется нечеткое

отношение

π =

, обозначаемое

π = ϕ ∩ψ

, åñëè

=

. При этом для любых

справед-

ëèâî

<

>=

<

>

<

> .

Определение 16. Дополнением отношения

ϕ

называется нечеткое отно-

шение

←ϕ=

←

. При этом для любых

справедливо ¬

<

>=

−

<

> .

Определение 17. Инверсией отношения

ϕ

называется нечеткое отноше-

íèå

ϕ

−

=

−

, такое, что нечеткий график

−

представляет собой инверсию графика

. Ïðè ýòîì äëÿ

любых

справедливо

−

<

>=

<

> .

Определение 18. Композицией отношений

ϕ

èψ

называется нечеткое

отношение

=

, обозначаемое

= ϕ

ψ

, åñëè

=

. При этом для любых

справедли-

âî <

>= <

> <

> .

Пример 7. Пусть даны нечеткие отношения ϕ

è

ψ =

, графы которых показаны на рис. 12. Графы нечетких

отношений

ϕ ψ

,

ϕ ∩ψ

,

¬ϕ

,

ϕ

−

,

ϕ ψ

показаны на рис. 13.