
- •Электротехника
- •Содержание
- •Основы электробезопасности
- •Категорически запрещается !
- •Правила для студентов, работающих в лаборатории
- •Порядок выполнения лабораторной работы и отчёта
- •Электрические измерения и приборы (эип).
- •Измерение параметров электрической цепи.
- •Исследование неразветвленной электрической цепи синусоидального тока с различными видами нагрузки.
- •Частотные характеристики последовательного колебательного контура
- •Исследование разветвлённой электрической цепи синусоидального тока с различными видами нагрузки.
- •Исследование электрической цепи постоянного тока с линейными и нелинейными элементами.
- •Исследование трёхфазных цепей при соединении нагрузки по схеме «звезда»
- •Исследование трехфазных цепей при соединении нагрузки по схеме «треугольник»
- •Испытание однофазных трансформаторов
- •Испытание асинхронных двигателей в трёхфазном и однофазном режимах
- •Испытание двигателя постоянного тока параллельного возбуждения
- •Список литературы
Исследование неразветвленной электрической цепи синусоидального тока с различными видами нагрузки.
Цель работы
Исследовать цепь переменного тока при последовательном соединении приемников с различными видами нагрузок (R, L, C).
Исследовать явление резонанса напряжений.
Краткая теория
 Если
к цепи, состоящей из последовательно
соединённых активного сопротивления
R,
катушки индуктивности L
и
ёмкости С,
присоединить синусоидальное напряжение,
то в цепи установится синусоидальный
ток I(схема
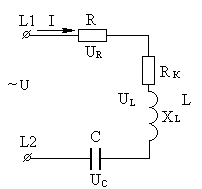
представлена нарис. 3.1).Общее напряжение
на зажимах цепи можно рассматривать
состоящим из суммы трёх слагаемых (на
основании второго закона Кирхгофа):
Если
к цепи, состоящей из последовательно
соединённых активного сопротивления
R,
катушки индуктивности L
и
ёмкости С,
присоединить синусоидальное напряжение,
то в цепи установится синусоидальный
ток I(схема
представлена нарис. 3.1).Общее напряжение
на зажимах цепи можно рассматривать
состоящим из суммы трёх слагаемых (на
основании второго закона Кирхгофа):
Рис. 3.1
падения напряжения на активном сопротивлении uR=i(R+RK);
где RK – активное сопротивление катушки индуктивности,
напряжения, уравновешивающего э.д.с. самоиндукции uL= εL;
напряжения, приложенного к зажимам конденсатора uC.
Тогда общеенапряжениедля цепи записывается:
для мгновенных значений напряжений u=uR+uL+uC;
для
комплексных значений напряжений ![]() =
=![]() +
+![]() +
+![]() . (3.1)
. (3.1)
В цепи последовательного соединения активного, индуктивного и ёмкостного сопротивлений вектор напряжения опережает вектор тока или отстаёт от него на угол сдвига фаз φ в зависимости от того, какой характер носит схема
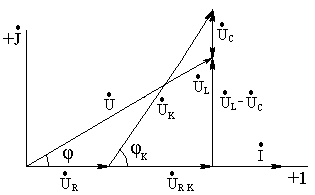
(ёмкостный или индуктивный). Векторная диаграмма цепи (с учётом
преобладающего влияния индуктивного сопротивления) имеет вид рис. 3.2.
 Вектор
активного напряжения
Вектор
активного напряжения
![]() =
=![]()
![]() совпадает
по фазе с вектором
совпадает
по фазе с вектором
![]() .Вектор
активного напряжения на катушке
индуктивности
.Вектор
активного напряжения на катушке
индуктивности
![]() также
совпадает по фазе с вектором тока
также
совпадает по фазе с вектором тока
![]() .
.
Рис.
3.2 Вектор
индуктивного напряжения
![]() =
=![]()
![]() XL
опережаетпо
фазе вектор тока
XL
опережаетпо
фазе вектор тока
![]() на четверть периода (или на угол + 900),
а вектор ёмкостного напряжения
на четверть периода (или на угол + 900),
а вектор ёмкостного напряжения
![]() =
=![]() (-
(-![]() XC)
отстаёт
от него по фазе на четверть периода (или
на угол − 900).
Векторы двух реактивных напряжений
XC)
отстаёт
от него по фазе на четверть периода (или
на угол − 900).
Векторы двух реактивных напряжений
![]() и
и
![]() в любой момент времени направлены
встречно друг другу. Величина общего
напряжения U
определяется
из векторной диаграммы рис. 3.2.
в любой момент времени направлены
встречно друг другу. Величина общего
напряжения U
определяется
из векторной диаграммы рис. 3.2.
U
=![]() =
I
=
I![]() ,
,
отсюда
I
=![]() =
=
![]() . (3.2)
. (3.2)
Полное сопротивление цепи
Z
=![]() . (3.3)
. (3.3)
Угол
сдвига фаз между вектором тока
![]() и
вектором общего напряжения
и
вектором общего напряжения
![]()
cos
φ
=
![]() =
=
![]() . (3.4)
. (3.4)
Рассмотрим некоторые частные случаи цепи последовательного соединения различных видов нагрузок.
1. Последовательное
соединение активного
сопротивления и
катушки
с сопротивлением ZK
=![]() .
(В схеме рис. 3.1 предполагают, чтоХС
=0).
Применяя второй закон Кирхгофа для
данной цепи, получим
.
(В схеме рис. 3.1 предполагают, чтоХС
=0).
Применяя второй закон Кирхгофа для
данной цепи, получим
![]() =
=![]() . (3.5)
. (3.5)
Напряжение
на зажимах катушки
![]() состоит
из активной составляющей
состоит
из активной составляющей
![]() и
индуктивной составляющей
и
индуктивной составляющей
![]() ,
, ![]() =
=![]() +
+![]() . (3.6)
. (3.6)
С учётом
уравнений (3.5) и (3.6) напряжение, приложенное
к рассматриваемой цепи
определяется ![]() =
=![]() (R+RK)+
(R+RK)+![]()
![]() XL=
XL=![]() +
+![]() .
.![]()
Абсолютное
значение приложенного напряжения
составит U
=
![]() =
=![]()
и величина
тока I
=![]()
![]() =
=![]() , (3.7)
, (3.7)
где Z-полное сопротивление всей цепи.
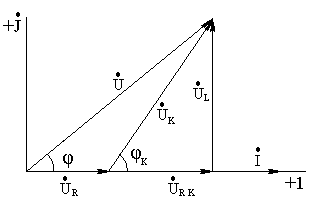 В
соответствии с уравнениями (3.5) и (3.6)
векторная диаграмма будет иметь вид
рис.3.3. Углы сдвига фаз определяются из
приведённых соотношений:
В
соответствии с уравнениями (3.5) и (3.6)
векторная диаграмма будет иметь вид
рис.3.3. Углы сдвига фаз определяются из
приведённых соотношений:
cos φ =
![]() =
=
![]() ;
;
sin φ
=![]() =
=![]() ;cos
φK=
;cos
φK=![]() =
=![]() ;
;
sin
φK
=
![]()
![]() .(3.8)
.(3.8)
Рис.3.3 Полученные соотношения могут быть использованы для вычислений активных и реактивных составляющих напряжения и сопротивлений по известным величинам тока, напряжения и мощности.
2. Последовательное
соединение
активного сопротивления и
конденсатора
с сопротивлением XC.
(В схеме рис. 3.1 предполагают , что
ZK=0).Напряжение
на зажимах данной цепи ![]() =
=![]() . (3.9)
. (3.9)
Величина
приложенного напряжения U
=![]() =
I
=
I![]() .
.
Ток в
цепи I
=![]() =
=![]() .
.
Векторная диаграмма рассматриваемой цепи имеет вид рис. 3.4.
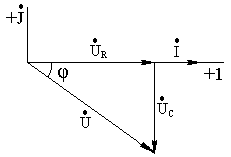 Из
диаграммы видно, что вектор напряжения
отстаёт по фазе от вектора тока на угол
φ,
который определяется из соотношений:
Из
диаграммы видно, что вектор напряжения
отстаёт по фазе от вектора тока на угол
φ,
который определяется из соотношений:
cos
φ =![]() =
=
![]() ;
;
sin
φ
=
![]() =
=
![]() . (3.10)
. (3.10)
Рис.3.4
3. Последовательное
соединение
катушки и
конденсатора
(в схеме рис. 3.1 предполагают, что R=0).
В
случае равенства индуктивного и
ёмкостного сопротивлений ХL
=
XC
в схеме возникает режим резонанса
напряжений. В этом случае реактивное
сопротивление равно нулю (Х
= ХL-XC
=
0),
полное сопротивление цепи оказывается
минимальным, равным активному сопротивлению
катушки Z
=![]() =RK.
=RK.
Ток в
цепи будет иметь максимальное значение I
=
![]() .
.
Приложенное
напряжение уравновешивается лишь
падением напряжения на активном
сопротивлении RK,
а угол сдвига фаз между током и напряжением
равен нулю (φ
=
0). сos
φ =
![]() =
1.
=
1.
В режиме резонанса напряжения на катушке и конденсаторе могут значительно превосходить приложенное напряжение, что опасно для обслуживающего персонала и может привести к повреждению изоляции электротехнической установки. Однако, явление резонанса получило широкое применение в радиотехнике, проводной связи и других областях техники, где применяются электрические фильтры.
Исходя
из условий резонанса напряжений ХL
=
XC,
т. е. L
=
![]() ,
,
получаем f
=
![]() . (3.11)
. (3.11)
Из этого уравнения следует, что резонанса напряжений можно достичь,
изменяя частоту f приложенного напряжения или регулируя индуктивность L или ёмкость С.
Применяя второй закон Кирхгофа для данной цепи, получим
![]() =
=![]() =
=![]()
![]() .
.
Векторная
диаграмма будет иметь вид рис.3.5. 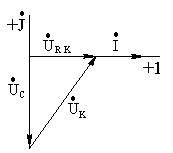
Из диаграммы видно, что при резонансе напряжения на катушке и конденсаторе могут быть равны только в случае идеальной катушки (RK = 0).
Рис.3.5
