- •Тема 8. Визначення переміщень у балках.
- •Розв’язання задач по темі “Визначення переміщень у балках”.
- •Тема 10. Контактні напруження.
- •Тема 11. Енергетичні методи визначення переміщень при довільному навантаженні.
- •Тема 12. Статично невизначувані балки.
- •Тема 13. Розкриття статичної невизначуваності рам за методом сил.
- •Тема 14. Складний опір.
- •Тема 15. Стійкість стиснених стержнів.
Тема 10. Контактні напруження.
Лекція 18. Стискання двох куль. Стискання двох циліндрів. Загальний випадок контакту двох тіл.
Контактні деформації і напруження виникають при взаємному натисканні двох стичних тіл на дуже малих площадках. Матеріал поблизу такої площадки зазнає об’ємного напруженого стану. Прикладом об’ємного напруженого стану може бути робота матеріалу в процесі передавання зусилля в шарикових і роликових підшипниках, зубчастих колесах, елементах кулачкових механізмів. Теорія розподілу контактних напружень (контактна задача) була розроблена методом теорії пружності Герцем (1885 р.). Визначення контактних напружень в інженерній практиці дуже важливо при розрахунку шарикових і циліндричних підшипників, а також при розрахунку кульових і циліндричних катків в опорних вузлах. Слід зауважити, що напруження в міру віддаляння від місця контакту швидко зменшується, а тому контактні напруження мають місцевий характер.
Нижче наведено залежності для напружень, переміщень і розмірів площинок стикання, які ґрунтуються на рівняннях плоскої задачі теорії пружності.
1. Стискання двох куль. При взаємному стисканні силами Р двох куль, радіуси яких R1 і R2 (рис.10.1), утворюється кругла площадка контакту, радіус якої позначаємо через а.
Із
умов симетрії можна установити, що епюра
стискуючого напруження по площадці
контакту буде симетрична відносно осі
Z
і
максимальна інтенсивність по осі Z
буде σmax
.
Із умови рівноваги маємо

Рис. 10.1
 .
.
Звідки
 ,
тобто максимальне напруження на поверхні
контакту дорівнює 1,5 σср,
де – σср
середнє напруження.
,
тобто максимальне напруження на поверхні
контакту дорівнює 1,5 σср,
де – σср
середнє напруження.
Методом теорії пружності знайдено радіус площадки контакту
 , (1)
, (1)
де Е1 і Е2 - модулі пружності матеріалів куль. Нормальні (стискальні) напруження на площадці контакту розподілені по півсфері.
Найбільше нормальне напруження розміщено в центрі площадки контакту і визначається за формулою
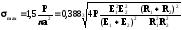 . (2)
. (2)
Головні стискуючі напруження, що діють на грані вирізаного паралелепіпеда (рис.10.1.б), дорівнюють

Рис. 10.2
 ;
;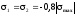 .
.
Визначимо напруження в центрі площадки контакту за четвертою теорією міцності:
 .
.
Звідки
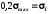 ,
, .
.
Встановлено, що найнебезпечніша точка лежить на осі Z приблизно на глибині, що дорівнює половині радіуса площадки контакту. Головні напруження в цій точці дорівнюють:
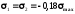 ,
, .
.
Якщо
в формулі (2) брати не суму, а різницю
R1-R2,
отримаємо
значення
 для
розрахункового випадку тиску кулі на
угнуту сферичну поверхню (рис.10.2)
для
розрахункового випадку тиску кулі на
угнуту сферичну поверхню (рис.10.2)
 . (3)
. (3)
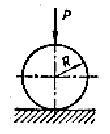
Рис.10.3
У випадку, коли стискається куля і площина (рис.10.3), тобто R2=∞, R1=R, отримаємо для напруження такий вираз:
 .
.
2. Стискання двох циліндрів. При взаємному стиску двох циліндрів з паралельними твірними рівномірно розподіленим навантаженням q, Н/м (рис.10.4), утворюються прямокутні площадки контакту шириною в. Параметр в визначається за формулою:
Рис. 10.4

 , (4)
, (4)
де Е1, Е2 – модулі пружності матеріалів циліндрів. Найбільше стискуюче напруження, що виникає в точках осі площадки контакту, визначається за формулою
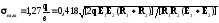 . (5)
. (5)
Слід
відзначити, що небезпечна точка матеріалу
лежить на вертикальній осі Z
на
глибині
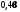 .
Головні напруження в цій точці будуть
такі:
.
Головні напруження в цій точці будуть
такі:
 ,
, ,
,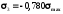 .
.
Наведені формули отримані при µ=0,3.
Розрахунки
на міцність матеріалів при контактних
напруженнях проводяться за третьою або
четвертою теоріями міцності. Якщо
підставити у вирази для теорій міцності
значення головних напружень у небезпечній
точці, виражені через
 в центрі площадки контакту, то умови
міцності можна записати так:
в центрі площадки контакту, то умови
міцності можна записати так:
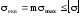 ,
,
звідки
 ,
,
де

 - допустиме значення найбільшого
напруження в місці контакту.
- допустиме значення найбільшого
напруження в місці контакту.
Значення
коефіцієнта m
залежить від відношення півосей
еліптичної площадки контакту і вибраної
теорії міцності. Допустимі значення
контактних напружень наведені в
довідниках з міцності конструкцій.
Наприклад, для шарикових і роликових
підшипників із хромистої сталі беруть
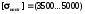 МПа.
МПа.
3.
Загальний випадок контакту двох тіл.
Розглянемо тепер загальний випадок
контакту двох тіл, верхнє з яких має
головні радіуси кривизни в точці дотику
першого тіла
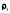 і
і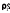 ,
а нижнє –
,
а нижнє – і
і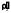 (рис10.5). Обидва тіла в точці дотику мають
загальну дотичну площину АВ і загальну
нормальZ.
Уздовж нормалі Z
спрямовані сили Р. Головними кривизнами
криволінійної поверхні називають
найбільшу і найменшу її кривизни,
розташовані в двох взаємно перпендикулярних
площинах. Тут
(рис10.5). Обидва тіла в точці дотику мають
загальну дотичну площину АВ і загальну
нормальZ.
Уздовж нормалі Z
спрямовані сили Р. Головними кривизнами
криволінійної поверхні називають
найбільшу і найменшу її кривизни,
розташовані в двох взаємно перпендикулярних
площинах. Тут
 ,
, .
.
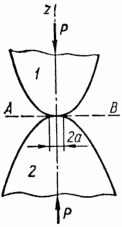
Рис. 10.5
Радіуси
кривизни є додатними, якщо центри
кривизни розташовані усередині тіла.
Позначимо через φ кут між головними
площинами кривизни тіл, в яких лежать
менші радіуси
 і
і .
.
У загальному випадку поверхня контакту в місці стикання двох тіл з одного матеріалу обмежена еліпсом з півосями
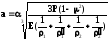 ;
;
 ,
,
де μ - коефіцієнт Пуассона.
Тут коефіцієнти α і β є функції допоміжного кута ψ, що визначається за формулою
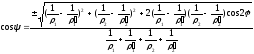 .
.
Знак чисельника у цьому виразі вибирають так, щоб cosψ був додатним.
Найбільше напруження стискання в центрі еліпса на поверхні стискання визначається за формулою:
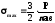 .
.
Найбільш
небезпечна точка знаходиться на осі Z
на
деякій глибині, яка залежить від
відношення
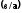 .
.
Але
найбільше дотичне напруження в небезпечній
точці дорівнює
 і не залежить від відношення
і не залежить від відношення .
Звернемо увагу на те, що контактні
напруження залежать від пружних сталих
матеріалу.
.
Звернемо увагу на те, що контактні
напруження залежать від пружних сталих
матеріалу.
Досліди показують, що формули для розмірів площинки стискання і зближення тіл, що стискаються, справедливі з достатньою точністю, поки навантаження, яке прикладене до цих тіл, не викликає у місці стискання залишкового деформування.
Значення коефіцієнтів α і β знаходимо в такій таблиці:
|
|
α |
β |
|
α |
β |
|
20 |
3,778 |
0,408 |
60 |
1,486 |
0,717 |
|
30 |
2,731 |
0,493 |
65 |
1,378 |
0,759 |
|
35 |
2,397 |
0,530 |
70 |
1,284 |
0,802 |
|
40 |
2,136 |
0,567 |
75 |
1,202 |
0,846 |
|
45 |
1,926 |
0,604 |
80 |
1,128 |
0,893 |
|
50 |
1,754 |
0,641 |
85 |
1,061 |
0,944 |
|
55 |
1,611 |
0,678 |
90 |
1,000 |
1,000 |
Розв’язання задач по темі “Контактні напруження”.
Задача 10.1. Шарик підшипника зазнає найбільшої стискуючої сили Р=100 Н. Вважаючи, що шарик підшипника розміщено на вгнутій сфері радіуса R=100 мм, визначити розміри площі контакту, а також найбільше напруження в центрі площі контакту. Перевірити міцність шарикопідшипника за четвертою теорією міцності, якщо діаметр шарика d=20 мм, матеріал шарика і сферичної поверхні виготовлені із сталі 30ХГСА, для якої [σ]=1000 МПа, Е=2,1∙105 МПа.
Розв’язання.
Стиск
шарика, який розміщений на вгнутій
сферичній поверхні, зображено на
рис.10.2, де
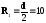 мм,
мм, мм.
мм.
Розміри контакту а=r (радіус круглої площадки) визначимо за формулою (1), якщо Е1=Е2=Е:
 м=
=0,193 мм.
м=
=0,193 мм.
Найбільше напруження на цій площадці знайдемо згідно виразу
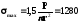 МПа.
МПа.
Головні напруження в найбільш небезпечній точці шарикопідшипника будуть такі:
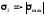 ;
;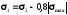 .
.
Підставивши значення головних напружень σ1, σ2, σ3 у вираз для четвертої теорії міцності
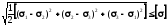 ,
,
отримаємо:
 ,
,
або
 МПа,
тобто
МПа,
тобто МПа.
МПа.
Оскільки
 МПа
менше
за допустиме
МПа
менше
за допустиме
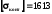 МПа,
то міцність
шарикопідшипника забезпечена.
МПа,
то міцність
шарикопідшипника забезпечена.
Задача 10.2. Упорний шариковий підшипник з плоскими кільцями без жолобків (рис.10.6) статично стиснутий силами Q=6,4 кН. Визначити розміри площадки контакту між шариком і кільцем та найбільше напруження на цій площадці; перевірити міцність. Діаметр шарика d=15 мм; кількість шариків і=20; коефіцієнт нерівномірності розподілу навантаження між окремими шариками підшипника – 0,8. Матеріал шариків і кілець – хромиста сталь; допустиме найбільше напруження в місці контакту [σконт]=3500 МПа; модуль пружності Е=2,12∙105 МПа.
Розв’язання. З урахуванням нерівномірності розподілу навантаження між окремими шариками визначимо силу, яка стискає шарик:
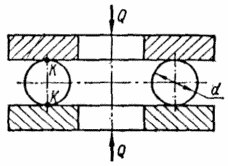
Рис. 10.6
 кН.
кН.
У місцях контакту кілець і шариків (рис.10.6) точки К виникає кругла площадка, радіус якої згідно виразу (1) дорівнює
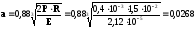 см.
см.
В
даному випадку
 см;
см; ,
Е1=Е2=Е.
,
Е1=Е2=Е.
Найбільше напруження на площадці контакту визначимо за формулою:
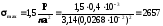 МПа.
МПа.
Таким
чином,
 .
.