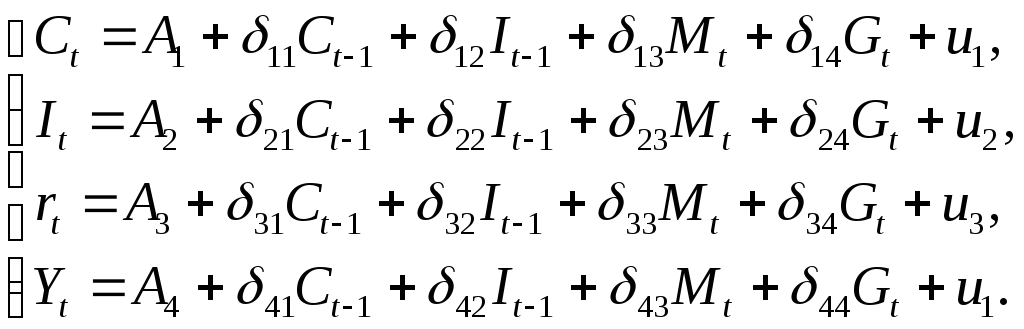- •Учебно-методический комплекс
- •1. Учебная программа дисциплины - syllabus
- •1.6. График выполнения и сдачи заданий по дисциплине
- •1.7. Список литературы
- •Интернет источники:
- •1.8. Информация об оценке
- •1.9. Политика и процедура курса
- •2. Учебно-методические материалы по дисциплине
- •2.1. Тематический план курса
- •2.2. Тезисы лекционных занятий
- •Тема № 8 .Парная нелинейная регрессия
- •Гипербола
- •Экспонента
- •Парабола
- •Тема №12 Система одновременных уравнений
- •2.3. Планы семинарских занятий
- •Тема 12. (занятие 15) Система одновременных уравнений
- •Методы оценки параметров структурной формы модели
- •2.5. Планы занятий в рамках самостоятельной работы студентов под руководством преподавателя
- •Линейная регрессия.
- •Проверка общего качества уравнения регрессии. Коэффициент детерминации r2
- •Множественная линейная регрессия
- •Функция линейн()
- •Использование f-cтатистики
- •2.6. Планы занятий в рамках самостоятельной работы студентов
- •Проверка значимости оценок коэффициентов регрессии. Статистика Стьюдента.
- •Вычисление t-статистики
- •2.7. Тематика письменных работ по курсу
- •2.8. Тестовые задания для самоконтроля
- •Приложение 2 Критические точки распределения Стьюдента
- •Приложение 3 Критические точки распределения Фишера-Снедекора (k1 — число степеней свободы большей дисперсии, к2 — число степеней свободы меньшей дисперсии)
- •Приложение 4 Критические точки распределения 2«хи – квадрат»
- •Учебно-методический комплекс
Тема 12. (занятие 15) Система одновременных уравнений
Разберите пример.
Изучается модель вида
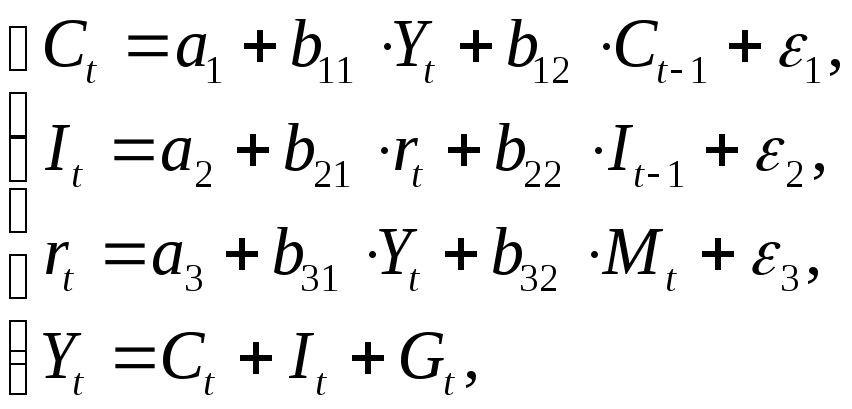
где
![]() – расходы на потребление в период
– расходы на потребление в период![]() ,
,
![]() –совокупный
доход в период
–совокупный
доход в период
![]() ,
,
![]() –инвестиции
в период
–инвестиции
в период
![]() ,
,
![]() –процентная
ставка в период
–процентная
ставка в период
![]() ,
,
![]() –денежная
масса в период
–денежная
масса в период
![]() ,
,
![]() –государственные
расходы в период
–государственные
расходы в период
![]() ,
,
![]() –расходы
на потребление в период
–расходы
на потребление в период
![]() ,
,
![]() инвестиции
в период
инвестиции
в период
![]() .
.
Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение – функция денежного рынка, четвертое уравнение – тождество дохода.
Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию.
Модель
включает четыре эндогенные переменные
![]() и четыре предопределенные переменные
(две экзогенные переменные –
и четыре предопределенные переменные
(две экзогенные переменные –![]() и
и![]() и две лаговые переменные –
и две лаговые переменные –![]() и
и![]() ).
).
Проверим необходимое условие идентификации для каждого из уравнений модели.
Первое
уравнение:
![]() содержит две эндогенные переменные
содержит две эндогенные переменные![]() и
и![]() и одну предопределенную переменную
и одну предопределенную переменную![]() .
Таким образом,
.
Таким образом,![]() ,
а
,
а![]() ,
т.е. выполняется условие
,
т.е. выполняется условие![]() .
Уравнение сверхидентифицируемо.
.
Уравнение сверхидентифицируемо.
Второе
уравнение:
![]() включает две эндогенные переменные
включает две эндогенные переменные![]() и
и![]() и одну экзогенную переменную
и одну экзогенную переменную![]() .
Выполняется условие
.
Выполняется условие![]() .
Уравнение сверхидентифицируемо.
.
Уравнение сверхидентифицируемо.
Третье
уравнение:
![]() включает две эндогенные переменные
включает две эндогенные переменные![]() и
и![]() и одну экзогенную переменную
и одну экзогенную переменную![]() .
Выполняется условие
.
Выполняется условие![]() .
Уравнение сверхидентифицируемо.
.
Уравнение сверхидентифицируемо.
Четвертое
уравнение:
![]() .
Оно представляет собой тождество,
параметры которого известны. Необходимости
в идентификации нет.
.
Оно представляет собой тождество,
параметры которого известны. Необходимости
в идентификации нет.
Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.
|
|
|
|
|
|
|
|
|
|
|
I уравнение |
–1 |
0 |
0 |
|
|
0 |
0 |
0 |
|
II уравнение |
0 |
–1 |
|
0 |
0 |
|
0 |
0 |
|
III уравнение |
0 |
0 |
–1 |
|
0 |
0 |
|
0 |
|
Тождество |
1 |
1 |
0 |
–1 |
0 |
0 |
0 |
1 |
В соответствии с достаточным условием идентификации ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели без одного.
Первое уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
|
|
|
|
|
|
|
|
II уравнение |
–1 |
|
|
0 |
0 |
|
III уравнение |
0 |
–1 |
0 |
|
0 |
|
Тождество |
1 |
0 |
0 |
0 |
1 |
Ранг
данной матрицы равен трем, так как
определитель квадратной подматрицы
![]() не
равен нулю:
не
равен нулю:
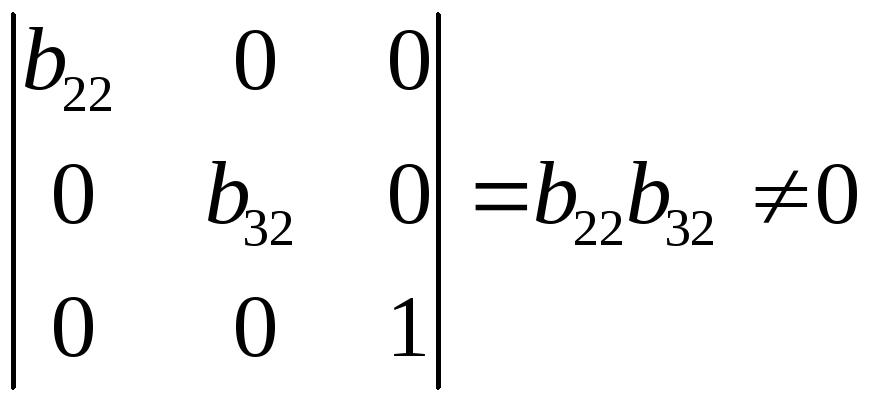 .
.
Достаточное условие идентификации для данного уравнения выполняется.
Второе уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
|
|
|
|
|
|
|
|
I уравнение |
–1 |
|
|
0 |
0 |
|
III уравнение |
0 |
|
0 |
|
0 |
|
Тождество |
1 |
–1 |
0 |
0 |
1 |
Ранг
данной матрицы равен трем, так как
определитель квадратной подматрицы
![]() не
равен нулю:
не
равен нулю:
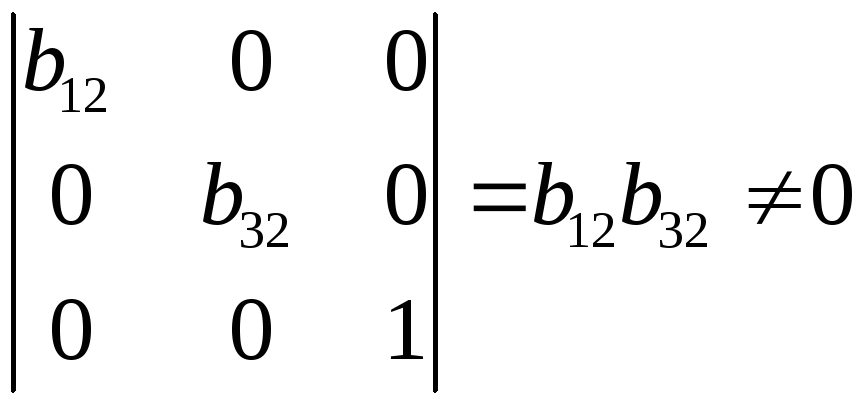 .
.
Достаточное условие идентификации для данного уравнения выполняется.
Третье уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
|
|
|
|
|
|
|
|
I уравнение |
–1 |
0 |
|
0 |
0 |
|
II уравнение |
0 |
–1 |
0 |
|
0 |
|
Тождество |
1 |
1 |
0 |
0 |
1 |
Ранг
данной матрицы равен трем, так как
определитель квадратной подматрицы
![]() не равен нулю:
не равен нулю:
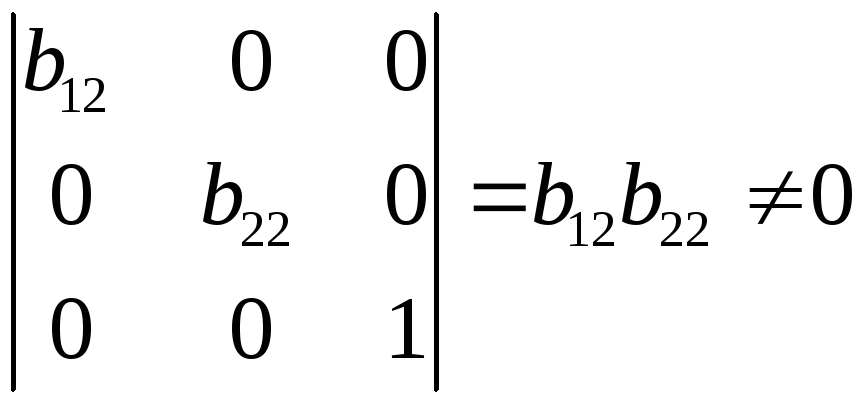 .
.
Достаточное условие идентификации для данного уравнения выполняется.
Таким образом, все уравнения модели сверхидентифицируемы. Приведенная форма модели в общем виде будет выглядеть следующим образом: