
- •Часть I. Финансовый анализ в условиях определенности. Попова н.В.
- •1.1. Методы наращения и дисконтирования денежных сумм. Основные определения и формулы.
- •Если доход определяется операцией наращения, то проценты вычисляют по формуле
- •Методы наращения по ставке I.
- •Наращение по учетной ставке.
- •Сравнение методов наращения.
- •Свойства наращенной суммы долга.
- •Сравнение методов дисконтирования.
- •Свойства современной величины суммы погашаемого долга.
- •Эквивалентность процентных ставок.
- •Номинальные и эффективные процентные ставки.
- •Переменные процентные ставки.
Переменные процентные ставки.
В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки. В инвестиционных расчетах понятие переменной процентной ставки является одним из важнейших.
Определение. Процентная ставка называется переменной, если она изменяет свое значение в течение срока долга.
Рассмотрим дискретные переменные процентные ставки. Пусть n - срок долга, n = n1 + n2 + … + nk , где nj - период в сроке долга, когда применяется процентная ставка ij или учетная ставка dj, j = 1,2,…, k.
1) Наращение и дисконтирование по простой переменной процентной ставке.
Согласно формуле (1.8), проценты за каждый период nj в сроке долга составляют
![]() .
.
Проценты за весь срок долга
![]() .
.
Тогда наращенная сумма к концу срока долга n составит:
 .
(1.52)
.
(1.52)
Предположим, что известна сумма погашаемого долга Sn. Формула современной величины суммы Sn при математическом ее учете по простой переменной процентной ставке имеет вид:
 .
(1.53)
.
(1.53)
Применяя формулу (1.20) последовательно для периодов nk, nk – 1, …,n2 , n1, получим формулу современной величины суммы Sn при банковском ее учете по простой переменной учетной ставке:
 .
(1.54)
.
(1.54)
Соответственно, формула наращенной суммы долга по простой переменной учетной ставке имеет вид:
 . (1.55)
. (1.55)
2) Наращение и дисконтирование по сложной переменной процентной ставке.
Применяя формулу (1.13) последовательно для каждого периода наращения n1, n2, … , nk , получаем формулу наращенной суммы долга по переменной сложной процентной ставке:
![]() .
(1.56)
.
(1.56)
Если известна сумма погашаемого долга Sn, то, применяя формулу (1.17) или (1.21) последовательно для каждого периода дисконтирования nk, nk – 1, … , n2, n1, получим формулы приведенной к моменту t = 0 величины суммы Sn при математическом и банковском ее учете по сложной переменной процентной ставке:
 .
(1.57)
.
(1.57)
![]() .
(1.58)
.
(1.58)
Формулы (1.40) и (1.43) можно рассматривать как формулы наращения суммы долга по переменным эффективным и номинальным процентным ставкам.
Пример 1.15. Ожидаемая эффективная процентная ставка на первый год – 10 %, на второй – 12 %, на третий и четвертый – 14 %. В конце четвертого года заемщик обязуется погасить долг в размере 2000 д.е. Какова может быть сумма кредита?
Примем за единицу измерения времени 1 год. Тогда по формуле (1.57) получаем
![]() =
1249,14 (д.е.).
=
1249,14 (д.е.).
3) Наращение и дисконтирование по непрерывным переменным процентным ставкам. Переменную непрерывную процентную ставку δ(t) называют интенсивностью процентов или силой роста в единицу времени в момент t. Формула наращенной суммы долга при непрерывном начислении процентов, когда интенсивность процентов δ(t) является функцией времени, имеет вид (1.46):
![]() .
.
Задавая конкретный вид зависимости δ(t), моделируют поведение интенсивности процентов во времени. Рассмотрим наиболее часто используемые формулы для δ(t). Для этого введем обозначения. Обозначим через F(t) и ν(t) множитель наращения и дисконтный множитель соответственно по переменной силе роста δ(t) в момент t, где t ≥ 0. F(t) – это накопление (стоимость) в момент t единичного вклада, сделанного в момент t = 0. ν(t) - это современная стоимость 1 д.е., подлежащей выплате в момент t. Для вклада, сделанного в момент t = 0, множитель наращения в момент t имеет вид:
![]() .
(1.59)
.
(1.59)
Тогда дисконтный множитель в момент t равен
![]() (1.60)
(1.60)
Если δ(t) интегрируема, то F(t) и ν(t) являются непрерывными функциями времени t. В случае, когда интенсивность процентов является постоянной величиной, т.е. δ(t) = δ для всех t, множитель наращения и дисконтный множитель имеют вид F(t) = eδt и ν(t) = e–δt. Наращенная сумма долга в момент t может быть найдена по формуле
![]() , (1.61)
, (1.61)
где P0 - первоначальная сумма долга в момент t = 0. Современная стоимость суммы St, подлежащей выплате в момент t, равна
![]() .
(1.62)
.
(1.62)
1. δ(t) - линейная функция времени, т.е. δ(t) = δ0 + at.
Здесь δ0 – начальное значение силы роста, a - годовой прирост силы роста. Так как a = δ(t + 1) – δ(t), то a может быть положительным, отрицательным или равно нулю, т.е. возможны значения a > 0, a < 0, a = 0. Значение a = 0 соответствует постоянной силе роста δ0. График зависимости интенсивности процентов от времени имеет вид, показанный на рис. 1.1.5.

Рис. 1.1.5
Как видим, в случае,
когда предполагается линейное уменьшение
интенсивности процентов, срок долга не
должен превышать величину
![]() ,
гдеa
< 0.
,
гдеa
< 0.
Рассмотрим поведение множителя наращения для всех трех случаев. Так как
![]() ,
,
то
![]() . (1.63)
. (1.63)
Отсюда следует,
что
![]() для каждогоt,
причем
F(t)
= 1 в момент t
= 0. Если a
≥ 0, то
для каждогоt,
причем
F(t)
= 1 в момент t
= 0. Если a
≥ 0, то
![]() ,
,![]() .Характер
зависимости множителя наращения F(t)
от времени для случаев, когда a
>
0 и a
= 0 показан на рис. 1.1.6. При a
= 0 множитель наращения имеет вид
.Характер
зависимости множителя наращения F(t)
от времени для случаев, когда a
>
0 и a
= 0 показан на рис. 1.1.6. При a
= 0 множитель наращения имеет вид
![]() .
.
Если a
< 0, то производная
![]() в точке
в точке![]() изменяет свой знак с“+”
на “–“
, а функция F(t)
в этой точке достигает своего максимального
значения, причем
изменяет свой знак с“+”
на “–“
, а функция F(t)
в этой точке достигает своего максимального
значения, причем
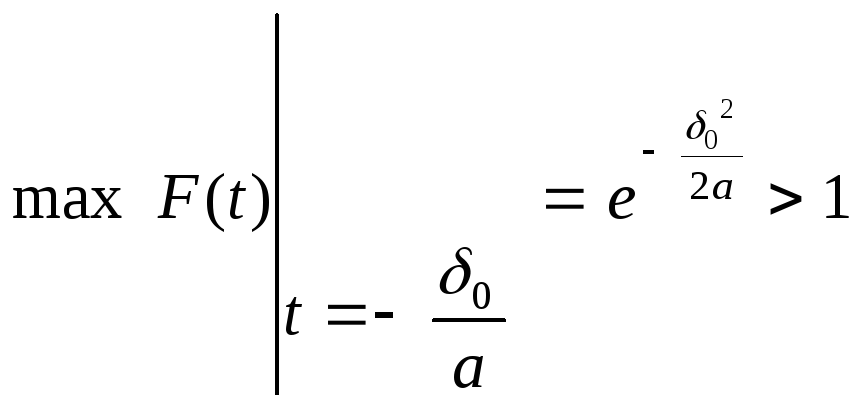 .
.
Из этого в частности
следует, что задача об увеличении суммы
долга в число раз, превышающее значение
![]() ,
в случаеa
< 0 является некорректной. При
построении графика функции F(t)
учтем, что при
a
< 0 множитель наращения F(t)
≥ 1, если
,
в случаеa
< 0 является некорректной. При
построении графика функции F(t)
учтем, что при
a
< 0 множитель наращения F(t)
≥ 1, если
![]() ,
т.е.
,
т.е.![]() и
и![]() .
График зависимости множителя наращения
F(t)
от времени при a
< 0, приведен на рис. 1.1.6. Поведение
множителя наращения в этом случае
показывает, что процесс наращения суммы
долга прекращается в момент
.
График зависимости множителя наращения
F(t)
от времени при a
< 0, приведен на рис. 1.1.6. Поведение
множителя наращения в этом случае
показывает, что процесс наращения суммы
долга прекращается в момент
![]() ,
что подтверждает ранее сделанный вывод
о сроке долга дляa
< 0.
,
что подтверждает ранее сделанный вывод
о сроке долга дляa
< 0.

Рис. 1.1.6
Пример 1.16. Предполагается, что годовая интенсивность процентов - линейная функция времени. Начальное значение силы роста равно 0,1. Годовой прирост интенсивности процентов составляет: а) 0,025; б) 0; в) - 0,025. Рассчитать значения множителя наращения для следующих сроков долга: 3, 4, 5, 6, 7, 8, 9 лет.
Согласно условию, δ(t) = δ0 + at. Здесь δ0 = 0,1. Значения параметра a следующие: а) a = 0,025; б) a = 0; в) a = – 0,025. Множитель наращения в каждом из трех случаев имеет вид:
а)
![]() ; б)
; б)![]() в)
в)![]() .
.
Значения множителей наращения для указанных сроков приведены в таблице:
|
|
a |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
а) |
0,025 |
1,511 |
1,822 |
2,254 |
2,858 |
3,715 |
4,953 |
6,770 |
|
б) |
0 |
1,350 |
1,492 |
1,649 |
1,822 |
2,014 |
2,226 |
2,460 |
|
в) |
–0,025 |
1,206 |
1,221 |
1,206 |
1,162 |
1,091 |
1,000 |
0,894 |
Как видим, результаты
вычислений соответствуют характеру
кривых на рис. 1.1.6. В случае, когда a
= – 0,025 максимальное значение множителя
наращения равно
![]() = 1,221 и достигается оно при сроке долга,
равном
= 1,221 и достигается оно при сроке долга,
равном![]() = 4 года, что соответствует таблице.
= 4 года, что соответствует таблице.
Пример 1.17. 1 января 1998 года клиент положил в банк 1500 д.е. К 1 января 2002 года его вклад вырос до 1832,105 д.е. Предполагается, что интенсивность процентов в течение всего срока вклада являлась линейной функцией времени. Найти годовую интенсивность процентов на 1 января 2000 года.
Момент t
= 0 соответствует 1 января 1998 года.
Множитель наращения F(0)
= 1, F(4)
=
![]() .
Требуется найти интенсивность процентов
в моментt
= 2, т.е. δ(2).
Так как δ(t)
- линейная
функция времени (параметры которой
неизвестны), то
.
Требуется найти интенсивность процентов
в моментt
= 2, т.е. δ(2).
Так как δ(t)
- линейная
функция времени (параметры которой
неизвестны), то
![]() является квадратичной функцией.
Производная квадратичной функцииf(x)
обладает
следующим свойством:
является квадратичной функцией.
Производная квадратичной функцииf(x)
обладает
следующим свойством:
![]() .
.
Так как
![]() ,
,
то
![]()
является квадратичной функцией на отрезке [0, 4]. Тогда по свойству производной квадратичной функции
![]() .
.
Так как линейная функция является непрерывной, то по свойству интеграла с переменным верхним пределом
![]() .
.
Из последних двух равенств следует
![]() .
.
Так как t = 2, h = 2, то
![]() .
.
Этот ответ можно проверить. Значение F(4) совпадает со значением множителя наращения для 4-летнего срока долга в третьей строке таблицы предыдущего примера. По значениям параметров δ0 = 0,1 и a = – 0,025 для этой строки находим
δ(2) = δ0 + 2a = 0,05.
Следовательно, годовая интенсивность процентов на 1 января 2000 года была 0,05.
2. δ(t) - показательная функция времени, т.е. δ(t) = δ0 at .
Здесь δ0
– начальное значение силы роста, a
- годовой темп изменения силы роста. Так
как
![]() ,
то возможны значения
a
>
1, 0 < a
< 1, a
=1. Значение a
= 1 соответствует постоянной силе роста
δ0.
График зависимости интенсивности
процентов от времени имеет вид, показанный
на рис. 1.1.7 .
,
то возможны значения
a
>
1, 0 < a
< 1, a
=1. Значение a
= 1 соответствует постоянной силе роста
δ0.
График зависимости интенсивности
процентов от времени имеет вид, показанный
на рис. 1.1.7 .

Рис. 1.1.7
Из определения
параметра a
следует, что
![]() =a
– 1. Это
означает, что если предполагается
изменение интенсивности процентов по
показательному закону, то относительное
изменение силы роста за год является
величиной постоянной и равной a
– 1. Причем a
– 1 > 0,
если интенсивность процентов в единицу
времени возрастает, и
a
– 1 < 0, если интенсивность процентов
уменьшается.
=a
– 1. Это
означает, что если предполагается
изменение интенсивности процентов по
показательному закону, то относительное
изменение силы роста за год является
величиной постоянной и равной a
– 1. Причем a
– 1 > 0,
если интенсивность процентов в единицу
времени возрастает, и
a
– 1 < 0, если интенсивность процентов
уменьшается.
Рассмотрим
поведение множителя наращения для всех
трех случаев значений a.
Если a
= 1, то множитель наращения имеет вид
![]() .
Приa
>
0, a
≠
1 имеем
.
Приa
>
0, a
≠
1 имеем
![]() .
.
Тогда
![]() . (1.64)
. (1.64)
При
любом a
>
0 производная
![]() .
Значит, во всех трех случаяхF(t)
– возрастающая функция времени. Кроме
того,
.
Значит, во всех трех случаяхF(t)
– возрастающая функция времени. Кроме
того,
![]() ,
еслиa
≥
1. Чтобы
построить кривые наращения, преобразуем
выражение (1.64). Разложим at
в степенной ряд:
,
еслиa
≥
1. Чтобы
построить кривые наращения, преобразуем
выражение (1.64). Разложим at
в степенной ряд:
![]()
Так как
![]() ,
,
то
![]()
Отсюда следует,
что
![]()
![]() для каждогоt,
причем F(t)
= 1 в момент t
= 0. Кроме
того,
для каждогоt,
причем F(t)
= 1 в момент t
= 0. Кроме
того,
![]() при0
< a
< 1. Из
этого, в частности, следует, что задача
об увеличении суммы долга в число раз,
превышающих значение
при0
< a
< 1. Из
этого, в частности, следует, что задача
об увеличении суммы долга в число раз,
превышающих значение
![]() ,
в случае0
< a
< 1 является некорректной. Характер
зависимости множителя наращения F(t)
от времени показан на рис. 1.1.8.
,
в случае0
< a
< 1 является некорректной. Характер
зависимости множителя наращения F(t)
от времени показан на рис. 1.1.8.
Р ис.
1.1.8
ис.
1.1.8
Пример 1.18. Предполагается, что годовая интенсивность процентов - показательная функция времени. Интенсивность процентов а) увеличивается ежегодно на 10%; б) уменьшается ежегодно на 10%; в) остается постоянной. Начальное значение силы роста 0,1. Найти срок удвоения суммы долга.
Согласно
условию, δ(t)
= δ0at.
Здесь δ0
= 0,1. В
случае а) a
– 1 = 0,1. Следовательно a
= 1,1. В случае б) a
– 1 = –
0,1. Следовательно, a
= 0,9. В случае в) a
= 1. F(n)
= 2, где n
– искомый срок. Для случая б) рассчитаем
величину
![]() = 2,583>
2.
Следовательно, задача является корректной
и ее решение существует. Для случаев а)
и б) разрешим равенство
= 2,583>
2.
Следовательно, задача является корректной
и ее решение существует. Для случаев а)
и б) разрешим равенство
![]() относительноn:
относительноn:
 .
.
Разрешая
равенство
![]() относительноn,
получим для случая в):
относительноn,
получим для случая в):
![]() .
.
Тогда в случае а) n = 5,322 или 5 лет и 117 дней; в случае б) n = 12,438 или 12 лет и 160 дней; в случае в) n = 6,931 или 6 лет и 340 дней. Полученные значения сроков долга соответствуют характеру кривых наращения на рис. 1.1.8.
Замечание. Убедиться самостоятельно, что если F(n) = 3, то в случае б) задача не имеет решения.
Пример 1.19. Предполагается, что годовая интенсивность процентов - показательная функция δ(t) = 0,09(0,9)t. Найти современную стоимость 1000 д.е., подлежащих выплате через 3 года.
По формуле (1.60) дисконтный множитель, соответствующий данному закону изменения интенсивности процентов, имеет вид
![]() .
.
Тогда по формуле (1.62) находим современную стоимость 1000 д.е., подлежащих выплате через 3 года:
![]() .
.
3.
![]() -кусочно –
постоянная функция.
-кусочно –
постоянная функция.
Этот случай удобнее рассмотреть на конкретном примере. Предположим, что
 .
.
Кусочно-постоянная
функция является интегрируемой.
Найдем множитель наращения F(t).
Если
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Таким образом,
 .
.

Рис. 1.1.9
Предположим, время
измеряется в годах. Найдем наращенную
сумму вклада 100 д.е., произведенного в
момент t
= 0, через
4 года и через 12 лет. По формуле (1.61)
получаем
![]() , если срок долга
, если срок долга![]() ,
и
,
и![]() при
при![]() .
Тогда
.
Тогда![]() (д.е.)
и
(д.е.)
и![]() (д.е.).
(д.е.).
4) Формула Студли.
Еще один пример формулы для δ(t) является формула Студли, которая может быть записана следующим образом:
![]() . (1.65)
. (1.65)
Параметры p, r и s выбираются так, чтобы моделировать плавное убывание или плавное возрастание интенсивности процентов. Подробнее об этой формуле можно посмотреть в [3].
