
- •Часть I. Финансовый анализ в условиях определенности. Попова н.В.
- •1.1. Методы наращения и дисконтирования денежных сумм. Основные определения и формулы.
- •Если доход определяется операцией наращения, то проценты вычисляют по формуле
- •Методы наращения по ставке I.
- •Наращение по учетной ставке.
- •Сравнение методов наращения.
- •Свойства наращенной суммы долга.
- •Сравнение методов дисконтирования.
- •Свойства современной величины суммы погашаемого долга.
- •Эквивалентность процентных ставок.
- •Номинальные и эффективные процентные ставки.
- •Переменные процентные ставки.
Наращение по учетной ставке.
Если решается задача, обратная банковскому дисконтированию, то для нахождения суммы погашаемого долга пользуются учетной ставкой. Например, в этом возникает необходимость при определении суммы, которую надо проставить в векселе, если задана текущая сумма долга. Из формул (1.20), (1.21), (1.22), находим
![]() , (1.23)
, (1.23)
![]() ,
(1.24)
,
(1.24)
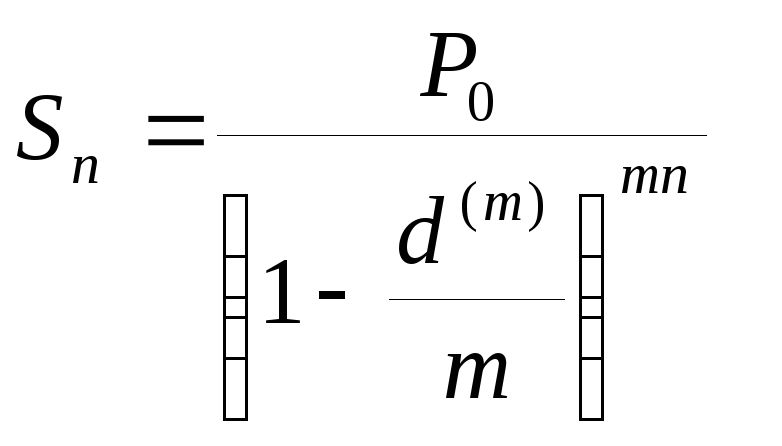 .
(1.25)
.
(1.25)
При непрерывном наращении по сложной учетной ставке справедлива формула (1.15) (при m → ∞ номинальные процентные ставки i(m) и d(m) перестают различаться).
Сравнение методов наращения.
Все рассмотренные методы наращения приведены в таблице.
|
Метод наращения |
Формула |
Множитель наращения |
|
По простой процентной ставке i |
|
|
|
По сложной процентной ставке i |
|
|
|
По номинальной процентной ставке i(m) |
|
|
|
По постоянной силе роста δ |
|
|
|
По номинальной учетной ставке d(m) |
|
|
|
По сложной учетной ставке d |
|
|
|
По простой учетной ставке d |
|
|
Определение. Число, показывающее во сколько раз наращенная сумма долга больше первоначальной, называется множителем наращения (или множителем накопления).
Экономический смысл множителя наращения заключается в следующем. Если срок долга n единиц времени, то множитель наращения показывает накопленную к моменту n будующую стоимость 1 д.е., вложенной в момент t = 0 на срок n. Очевидно, что множитель наращения больше 1. Интенсивность процесса наращения определяется множителем наращения. Сравнивая эти множители для каждого значения срока n, считая равными процентные ставки за 1 времени, можно сравнить темпы наращения по различным ставкам. Для этого рассмотрим отношения множителей наращения. Используем формулу разложения в степенной ряд функции
![]() .
.
Сравним темпы наращения по номинальной и простой процентным ставкам:

 .
(1.26)
.
(1.26)
Отсюда сразу получаем отношение множителей наращения по сложной (m = 1) и простой процентным ставкам:
 .
(1.27)
.
(1.27)
Сравним темпы наращения по номинальной процентной ставке в зависимости от m. Пусть 1 ≤ m1 < m2. Тогда

 (1.28)
(1.28)
для любого срока n. Следовательно, чем больше m, тем быстрее наращение по номинальной процентной ставке i(m). Самое быстрое наращение по номинальной процентной ставке производится по постоянной силе роста δ, когда m → ∞, а самое медленное наращение соответствует значению m = 1 (наращение по сложной процентной ставке).
Таким образом, имеем следующие соотношения множителей наращения по ставке i в зависимости от срока n:
![]() ;
;
![]() ;
(1.29)
;
(1.29)
![]() .
.
На рис. 1.1.1 показаны кривые наращения, соответствующие четырем методам наращения суммы долга по ставке i.
Р ис.1.1.1.
ис.1.1.1.
Рассмотрим сравнение темпов наращения по учетной ставке. Сравним множители наращения по простой и номинальной учетным ставкам :

 . (1.30)
. (1.30)
Отсюда получаем отношение множителей наращения по простой и сложной (m = 1) учетным ставкам:
 . (1.31)
. (1.31)
Сравним темпы наращения по номинальной учетной ставке в зависимости от m. Пусть 1 ≤ m1 < m2. Тогда

 (1.32)
(1.32)
для любого срока n. Следовательно, чем больше m, тем медленнее наращение по номинальной учетной ставке d(m). Самое медленное наращение по номинальной учетной ставке производится по постоянной силе роста δ , когда m → ∞, а самое быстрое наращение соответствует значению m = 1 (наращение по сложной учетной ставке).
Таким образом, имеем следующие соотношения множителей наращения по учетной ставке в зависимости от срока n:
 ;
;
 ;
(1.33)
;
(1.33)
 ;
;
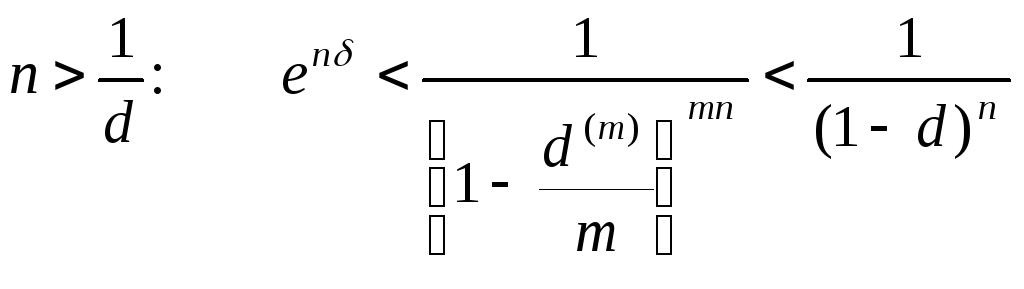 .
.
Н а
рис.1.1.2 показаны кривые наращения,
соответствующие четырем методам
наращения суммы долга по учетной ставке.
а
рис.1.1.2 показаны кривые наращения,
соответствующие четырем методам
наращения суммы долга по учетной ставке.
Рис. 1.1.2
Из неравенств (1.29) и (1.33) следует, что при заданном значении срока долга n наращение суммы долга по любой учетной ставке происходит быстрее наращения долга по любой из ставок i.


