14. Смешанное произведение. Координатная форма смешанного произведения.

4. Смешанное произведение векторов и его свойства. Выражение смешанного произведения через координаты векторов. Условия компланарности трех векторов.

Базис в пространстве называется правым, если (считая векторы имеющими общее начало) с конца третьего вектора мы видим кратчайший поворот от первого вектора ко второму против часовой стрелки. В противном случае базис называется левым.

Пространство называется ориентированным, если из двух классов базисов выбран один. Базисы этого класса называются положительно ориентированными.

Если пространство ориентировано, мы можем ввести определение смешанного произведенния.

Смешанным произведением векторов ,и(в данном порядке) называется число, равное оюъему ориентированного параллелепипеда, построенного на этих векторах, если они не компланарны; и равно нулю, если они компланарны.

Смешанное произведение векторов,иобозначается. При перестановке сомножителей в смешанном произведении может измениться только ориентация тройки векторов. Поэтому абсолютная величина смешанного произведенияне зависит от порядка сомножителей. Для любых векторов ,и, сравнивая ориентации тройки векторов, получаем:=====(2).

Предложение 1.

Каковы бы ни были векторы и, найдется едиснтвенный (не зависящий от) вектортакой, что при любомвыполнено равенство:(1).

Док-во: Сначала докажем существование вектора , а потом установим его единственность. Пусть векторыиколлинеарны. Тогда при любомвекторы,икомпланарны и=0. Поэтому мы можем положить. Раасмотрим неколлинеарные векторыии предположим сначала, что,инекомпланарны. Построим на них ориентированный параллелепипед и примем его за основание параллелограмм, построенный наи. Введем ориентацию на прямой OH, перпендикулярной основанию. Мы зададим её с помощью векторадлины 1, составляющего сиправую тройку,,. (Тройка,,также правая).- скалярная проекция векторана. По модулю она равна высоте параллелепипеда ОН, а знак её определяется ориентацией тройки,,.тогда и только тогда, когда концы векторовилежат в одном полупространстве, т.е. тройка,,- правая. Таким образом,положительно для правой тройки,,и отрицательно для левой.

Пусть положительное число S — площадь основания параллелепипеда. Тогда проивзедение по модулю равно объему параллелепипеда, а знак его совпадает со знаком. Это значит, что. Полученное равенство совпадает с (1), если(3). Осталось рассмотретьс лучай, когдаине коллинеарны, а,икомпланарны. В этом случаележит в плоскости векторови, следовательно, ортогонален вектору, вычисленному по формуле (2). Поскольку=0 и=0, вектор (3) удовлетворяет равенству (2) и в этом случае. Итак, мы нашли вектор, который удовлетворяет равенству (2) при любоми определяется только пои. Допустим, что для фиксированныхинашлось 2 вектораитаких, что для любоговыполнено равенство:и. отсюда следует, чтоили=0. Поэтому векторортогонален каждому вектору пространства и, следовательно, равен нулевому вектору. Это доказывает, что вектор, определяемый формулой (2), может быть только один. Предложение полностью доказано.

Теорема 3. Смешанное произведение векторов,ивыражается через их компоненты,ив произвольном базисепо ф-ле:=-*

Док-во: Заметим, что и умножим скалярно обе части на вектор. Мы получим=++, Учитывая рав-ва (1) и приводя подобные члены, получаем нужный нам результат.

Через детерминанты 3его порядка мы можем написать: =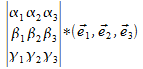(4)

Предложение 2. Равенство нулю детерминанта матрицы из компонент 3х векторов необоходимо и достаточно для компланарности векторов.

Док-во: это сразу следует из ф-лы (4), т.к.