10. Скалярные и векторные величины. Линейные операции операции с векторами.

Величины называют скалярными (скалярами), если они после выбора единиц измерения полностью характеризуются одним числом.

Если некоторая скалярная величина полностью определяется одним числом, не зависящим от выбора осей отсчета, то тогда говорят о чистой скалярной величине или об истинном скаляре.

Если некоторая скалярная величина определяется одним числом, абсолютная величина которого не зависит от выбора осей отсчета, а ее знак зависит от выбора положительного направления на осях координат, то тогда говорят о псевдоскалярной величине

Величина называется вектором (векторной), если она определяется двумя элементами различной природы: алгебраическим элементом - числом, показывающим длину вектора и являющимся скаляром, и геометрическим элементом, указывающим направление вектора.

Геометрически принято изображать вектор направленным отрезком. Зная координаты начала и конца вектора и, можно найти координаты вектора, определяемого этими точками, т.е. от координат конца вычитают координаты начала вектора.

Сложение и вычитание

Сложение и вычитание векторов производят геометрически.

Этот способ называют правилом треугольника.

Математически сложение записывают или, если речь идет о вычитании векторов.

Если в пространстве задано несколько векторов, число которых больше двух, то операцию сложения (вычитания) записывают как Геометрически этот способ называютправилом многоугольника.

Умножение вектора на скалярную величину. При умножении вектора на скаляр получают новый вектор , совпадающий по своему типу с исходным, длина (модуль) которого изменяется в раз, а направление совпадает с направлением исходного вектора , если  0, или противоположно исходному вектору, если  < 0. В координатной форме, если

, то .

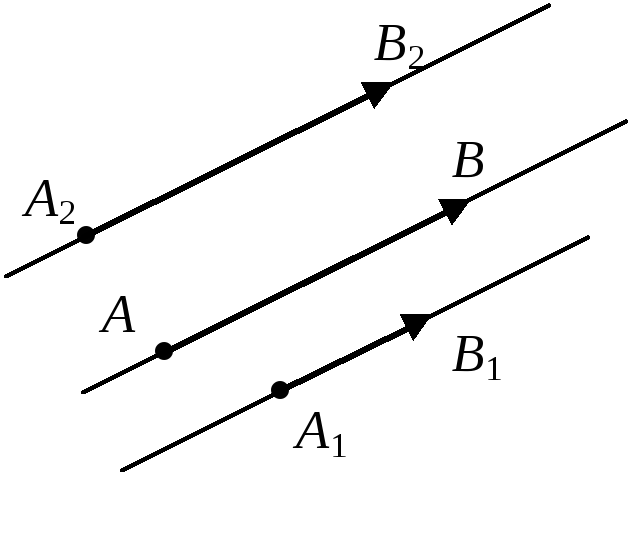
Два одинаково направленных и параллельных вектора называют коллинеарными. Коллинеарные векторы могут быть разной длины

Два вектора иназываютколлинеарными, если существуют такие два числа  и , не равные нулю одновременно, что выполняется равенство

Три вектора ,иназовемкомпланарными, если существуют такие три числа ,  и , не равные одновременно нулю, что выполняется равенство

11.Понятие базиса на плоскости и в пространстве. Ортонормированные базисы на плоскости и в пространстве. Координаты вектора в базисе.

Базисом на плоскости называются два неколлинеарных вектора на этой плоскости, взятые в определённом порядке (рис. 1.29). Эти векторыназываютсябазисными.

Пусть на плоскости задан базис . Построим прямыеи, содержащие базисные векторыисоответственно. Эти прямые пересекаются, так как базисные векторы неколлинеарные. Согласнопункт 1 теоремы 1.1, вектор можно представить в виде, где— проекция векторанавдоль;— проекция векторанавдоль, причем проекции определяются однозначно. Вектор, принадлежащий прямой, можно разложить по базисуна этой прямой (см. разд. 1.7), т.е. представить в виде , причем числоопределяется однозначно. Вектор, принадлежащий прямой, можно разложить по базисуна этой прямой (см. разд. 1.7), т.е. представить в виде , причем числоопределяется однозначно. Подставляя эти разложения в равенство, получаем

Теорема 1.4 (о разложении вектора по базису на плоскости). Любой вектор , принадлежащий плоскости, может быть разложен по базисуна этой плоскости, т.е. представлен в виде (1.3), где числаиопределяются однозначно.

Коэффициенты ив разложении (1.3) называютсякоординатами вектора а относительно базиса (числоназываютабсциссой, а —ординатой вектора ). Например, числа 2 и -3 являются координатами вектора(— абсцисса,— ордината вектора).

Базисные векторы , отложенные от одной (произвольной) точки плоскости, называютсярепером на плоскости.

Базис на плоскости называется правым (или, что то же самое, упорядоченная пара неколлинеарных векторов называется правой парой), если кратчайший поворот от первого вектора ко второму происходит против часовой стрелки (это направление поворота считается положительным). Базисные векторы (рис.1.30,а) правого базиса расположены соответственно как большой и указательный пальцы правой руки, если, смотреть на ее ладонь.

Левым базисом на плоскости (левой парой) называется такой базис, у которого кратчайший поворот от вектора к векторупроисходит по часовой стрелке (такое направление вращения считается отрицательным). Базисные векторы(рис. 1.30,6) левого базиса расположены соответственно как большой и указательный пальцы левой руки, если смотреть на ее ладонь.

Отметим следующее свойство: если неколлинеарные векторы образуют правую пару, то пары, получающиеся перестановкой векторов (пара) или заменой одного вектора противоположным (например, а), образуют левую пару.

Пример 1.9. В параллелограмме точкаделит сторонув отношении; точка— середина стороны;— точка пересечения медиан треугольника(рис. 1.31). Разложить векторыипо векторами.

Решение. Чтобы разложить вектор , применяем правило ломаной: векторзамыкает ломануюи ломаную.

Поэтому и, т.е..

Выразим все векторы этого равенства, за исключением искомого вектора , через векторыи.

Учитывая, что и, получаем.

Отсюда .Так как точка пересечения диагоналей параллелограмма делит каждую диагональ пополам, а точкаделит медианутреугольникав отношении, заключаем, что, т.е.

По правилу сложения векторов имеем . Следовательно, . Отсюда находим искомое разложение

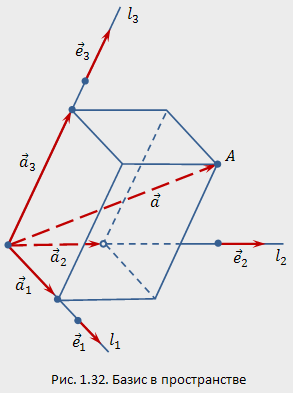
Базисом в пространстве называются три некомпланарных вектора , взятые в определённом порядке (рис.1.32). Эти векторыназываютсябазисными.

Пусть в пространстве задан базис . Построим прямые, содержащие базисные векторысоответственно. Без ограничения общности можно считать, что эти прямые пересекаются в одной точке (в противном случае можно было взять любые пересекающиеся в одной точке прямые, параллельные прямымсоответственно, поскольку проекции вектора на параллельные прямые равны (см. свойство 1 проекций в разд. 1.2.2)). Тогда любой векторможно однозначно представить в виде суммы своих проекций:, где— векторы, принадлежащие прямымсоответственно (см. п.2 теоремы 1.1). Раскладывая проекциипо базисам на соответствующих прямых (см. разд.1.3.1), находим:. Подставляя эти разложения в равенство, получаем

(1.4)

Теорема 1.5 (о разложении вектора по базису в пространстве). Любой вектор может быть разложен по базисув пространстве, т.е. представлен в виде (1.4), где числаопределяются однозначно.

Коэффициенты в разложении (1.4) называютсякоординатами вектора относительно базиса (число, называютабсциссой, — ординатой, а— аппликатой вектора а ). Например, числа являются координатами вектора(— абсцисса,— ордината,— аппликата вектора).

Базисные векторы , отложенные от одной (произвольной) точки, называютсярепером.

1. Базис на прямой, на плоскости, в пространстве определяется неоднозначно. Например, если — базис в пространстве, то система векторовпри любомтакже является базисом.

2. Следующие свойства выражают геометрический смысл линейной зависимости и линейной независимости векторов:

а) два (и более) коллинеарных вектора линейно зависимы, и наоборот, два линейно зависимых вектора коллинеарны; два линейно независимых вектора не коллинеарны;

б) три (и более) компланарных вектора линейно зависимы, и наоборот, три линейно зависимых вектора компланарны; три линейно независимых вектора не компланарны;

в) четыре (и более) вектора линейно зависимы.

Докажем, например, последнее свойство. Пусть — произвольные векторы. Если первые три векторалинейно зависимы, то и вся система— линейно зависима (см. свойство 6 в разд. 1.1.3). Если же векторылинейно независимы, то согласно пункту 2,"б" они не компланарны и, следовательно, образуют базис в пространстве. Тогда векторможно разложить по этому базису, т.е. представить в виде линейной комбинации векторов. В этом случае система векторовтакже линейно зависима (см. свойство 4 в разд. 1.1.3).

3. Понятие базиса непосредственно связано с понятием линейной независимости. Базис представляет собой упорядоченную совокупность линейно независимых векторов:

а) на прямой — это один линейно независимый вектор (см. пункт 1 замечаний 1.2);

б) на плоскости — это два линейно независимых вектора на этой плоскости, взятые в определённом порядке (см. пункт 2,"а");

в) в пространстве — это три линейно независимых вектора, взятые в определённом порядке (см. пункт 2,"б").

4. Теоремы 1.3-1.5 позволяют говорить, что базис — это полная система векторов (на прямой, на плоскости, в пространстве) в том смысле, что любой вектор (на прямой, на плоскости, в пространстве) линейно выражается через базисные векторы.

5. Теоремы 1.3-1.5 позволяют говорить, что базис — это максимальная линейно независимая система векторов (на прямой, на плоскости, в пространстве), так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.

6. Базис — это полная линейно независимая система векторов (на прямой, на плоскости, в пространстве).

Базис в пространстве называется правым (или, что то же самое, упорядоченная тройка некомпланарных векторов называется правой тройкой), если, наблюдая из конца третьего вектора, кратчайший поворот от первого вектора ко второму виден происходящим против часовой стрелки (рис.1.33,а). Если описанный поворот виден происходящим по часовой стрелке, то базис называется левым (упорядоченная тройка некомпланарных векторов называется левой тройкой) (рис. 1.33,6).

Отметим следующие свойства: если тройка некомпланарных векторов — правая, то тройки, получающиеся "циклической" перестановкой трех векторов— также правые, а тройки, получающиеся перестановкой двух векторов или заменой одного вектора противоположным (например,— левые).