12. Скалярное произведение. Координатная форма скалярного произведения.

Скалярным произведением двух векторов 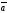и называется число, равное произведению длин этих векторов на косинус угла между ними:

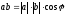. (2.3)

Скалярное произведение в координатной форме:

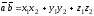. (2.4)

Из определения скалярного произведения следует, что

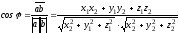. (2.5)

По значению косинуса находится угол между ненулевыми векторам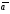и и .

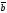Ненулевые векторы 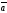и 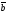перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю:

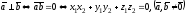. (2.6)

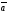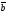Ненулевые векторы и коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны:

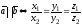. (2.7)

Проекция вектора 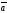на вектор 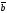вычисляется по формуле 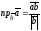. (2.8)

Примеры

1. Даны координаты точек , .

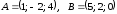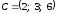Вычислить длину вектора

.

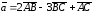Р е ш е н и е. Найдем координаты векторов по формуле (2.2):

.

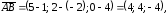
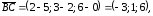
Найдем координаты вектора

=.

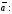
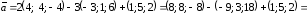
Тогда длина вектора 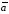находится по формуле (2.1):

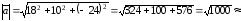31,6.

13. Векторное произведение. Координатная форма векторного произведения.

Векторным произведением векторов 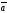и 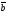называется вектор, обозначаемы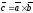й или 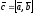, удовлетворяющий условиям:

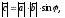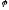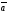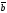
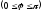1) где – угол между векторами и ; (2.9)

2) , ;

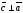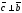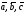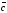3) упорядоченная тройка векторов – правая, т. е. если смотреть из конца вектора , то кратчайший поворот от вектора 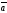к вектору 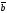осуществляется против хода часовой стрелки (в противном случае тройка называется левой).

Если хотя бы один из векторов 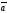и 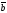нулевой, то полагают .

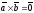Векторное произведение в координатной форме:

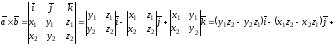
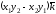+. (2.10)

Ненулевые векторы 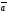и коллинерны тогда и только тогда, когда их векторное произведение равняется нулевому вектору; . (2.11)

Геометрический смысл векторного произведения: длина вектора 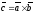векторного произведения векторов 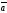и 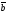численно равняется площади параллелограмма, построенного на векторах 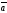и 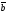, приведенных к общему началу.

14. Смешанное произведение. Координатная форма смешанного произведения.

Смешанным произведением трех векторов 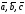называется число, обозначаемое 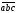или и равное скалярному произведению вектора 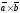на вектор : .

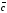Смешанное произведение векторов , , 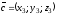в координатной форме:

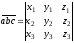. (2.12)

Ненулевые векторы 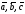компланарны тогда и только тогда, когда их смешанное произведение равняется нулю .

Геометрический смысл смешанного произведения: смешанное произведение трех векторов 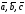численно равняется объему параллелепипеда, построенного на векторах 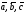(приведенных к общему началу), взятому со знаком «+», если тройка – правая, и взятому со знаком «–», если тройка 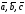– левая.