
- •Действия с матрицами: умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.
- •Определители 2-го и 3-го порядков. Свойства определителей.
- •Миноры и алгебраические дополнения. Вычисление определителей с помощью формул разложения.
- •Обратная матрица и ее вычисление.
- •Ранг матрицы. Вычисление ранга с помощью элементарных преобразований.
- •Системы линейных алгебраических уравнений. Матричный способ решения систем линейных алгебраических уравнений.
- •Теорема Кронекера-Капелли о совместности системы линейных алгебраических уравнений.
- •Формулы Крамера решения систем линейных алгебраических уравнений.
- •Метод Гаусса решения систем линейных алгебраических уравнений.
- •Скалярные и векторные величины. Линейные операции с векторами.
- •Понятие базиса на плоскости и в пространстве. Ортонормированные базисы на плоскости и в пространстве. Координаты вектора в базисе.
- •Скалярное произведение. Координатная форма скалярного произведения.
- •Векторное произведение. Координатная форма векторного произведения.
- •Смешанное произведение. Координатная форма смешанного произведения.
- •Уравнение прямой (на плоскости), уравнение плоскости, заданных точкой и нормальным вектором.
- •– Каноническое уравнение эллипса с центром в точке
- •Парабола и ее основные свойства.
- •Гипербола и ее основные свойства.
- •Прямые называются директрисами гиперболы. – левая директриса,
-
Формулы Крамера решения систем линейных алгебраических уравнений.
Рассмотрим еще один метод решения системы (1). Пусть, как и ранее, n = m.
Тогда из формулы (3) имеем:
Х= В
В


 =
=

 =
=



 .
(4)
.
(4)
В формуле (4)
 = det
A
– главный определитель системы (1),
= det
A
– главный определитель системы (1),

 =
(разлагаем по j-му
столбцу)=
=
(разлагаем по j-му
столбцу)=
=
 ;
;
 ,
– побочные определители системы (1).
,
– побочные определители системы (1).
Они получаются из главного определителя заменой соответствующего j-го столбца столбцом свободных членов. Формулы (4) называются формулами Крамера.
Алгоритм решения систем линейных алгебраических
уравнений с помощью формул Крамера
-
Для матрицы А системы уравнений вычислить ее главный определитель
 = det
A.
= det
A. -
Последовательно, заменяя каждый столбец матрицы А столбцом свободных членов, получить побочные определители
 ,
,
 .
. -
а) Если
 ≠ 0, то по формулам (4) определить
единственное решение системы (1):
≠ 0, то по формулам (4) определить
единственное решение системы (1):
 ,
,
 ,
….,
,
….,
 .
.
б) Если
 =0,
а хотя бы один из побочных определителей
=0,
а хотя бы один из побочных определителей
 ≠0,
то исходная система (1) несовместна, то
есть не имеет решений.
≠0,
то исходная система (1) несовместна, то
есть не имеет решений.
в) Если
 =
= =
0,
=
0,
 ,
то исходная система (1) имеет бесконечное
множество решений.
,
то исходная система (1) имеет бесконечное
множество решений.
Пример. Решить систему линейных алгебраических уравнений с помощью формул Крамера

Решение.
-
Матрица А имеет вид: А =
 ,
detA
=
,
detA
= =5
≠ 0,
=5
≠ 0,
Следовательно, система имеет единственное решение.
-
Найдем побочные определители системы:
 =10ּ
=10ּ
 +(–1)ּ
+(–1)ּ
 =10ּ5+5=55;
=10ּ5+5=55;
 =3ּ
=3ּ
 +10ּ
+10ּ
 =3ּ5–10ּ(–10)=115;
=3ּ5–10ּ(–10)=115;
 =(
упростим, сложив первую строку со второй
и
=(
упростим, сложив первую строку со второй
и
третью со второй)=
 =20
ּ
=20
ּ

 =20.
=20.
-
Метод Гаусса решения систем линейных алгебраических уравнений.
Рассмотрим еще один метод решения систем линейных алгебраических уравнений – метод Гаусса, который применим к любой системе линейных алгебраических уравнений. Иногда этот метод называют методом последовательного исключения неизвестных. Заметим, что при использовании этого метода мы также автоматически будем вычислять ранг матрицы системы.
Итак, пусть задана система m линейных алгебраических уравнений с n неизвестными:
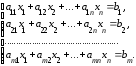 (6)
(6)
В матричном виде система (6) записывается АХ=В, где А – прямоугольная матрица размера mn:
А= ,
а Х и В – матрицы-столбцы: Х=
,
а Х и В – матрицы-столбцы: Х= ,
В=
,
В= .
.
Если в результате преобразований матрицы системы получится треугольная матрица, то система будет иметь вид:

где

Из
последнего уравнения можно найти
 ,
а затем, подставляя найденное
,
а затем, подставляя найденное
 в предпоследнее уравнение, найти
в предпоследнее уравнение, найти
 и т.д. В итоге будем иметь единственное
решение
и т.д. В итоге будем иметь единственное
решение
 ,
,
 ,
…,
,
…,
 .
В этом случае ранг матрицы А системы
уравнений равен n.
.
В этом случае ранг матрицы А системы
уравнений равен n.
Если в результате преобразований матрицы системы получится трапециевидная матрица, то система примет вид:

где

В этом случае k<n, следовательно, система уравнений будет неопределенной, то есть будет иметь бесконечное множество решений, так как она содержит n – k свободных переменных:

Придавая
свободным переменным
 ,
,
 ,
…,
,
…,
 произвольные значения, будем иметь
каждый раз новое решение исходной
системы уравнений, то есть решений будет
бесконечное множество. В этом случае
ранг матрицы А системы равен k.
произвольные значения, будем иметь
каждый раз новое решение исходной
системы уравнений, то есть решений будет
бесконечное множество. В этом случае
ранг матрицы А системы равен k.
Если в результате преобразований получено уравнение, в котором коэффициенты при всех неизвестных равны нулю, а свободный член отличен от нуля, то такая система будет несовместной, то есть не иметь решения.
Следует
отметить, что треугольная или трапециевидная
форма системы уравнений получалась
ввиду предположения, что коэффициенты отличны от нуля. Если же какой-либо из
этих коэффициентов равен нулю, то система
уравнений приобретет треугольную или
трапециевидную форму лишь после
надлежащего изменения нумерации
неизвестных.
отличны от нуля. Если же какой-либо из
этих коэффициентов равен нулю, то система
уравнений приобретет треугольную или
трапециевидную форму лишь после
надлежащего изменения нумерации
неизвестных.
В
заключение отметим, что метод Гаусса
применяется и для однородных систем
линейных алгебраических уравнений. В
этом случае, если получаем треугольный
вид системы уравнений, то она будет
иметь единственное (нулевое) решение
 =
= =
…=
=
…=
 =0,
если же получаем трапециевидный вид
системы, то будем иметь бесконечное
множество решений.
=0,
если же получаем трапециевидный вид
системы, то будем иметь бесконечное
множество решений.
При решении системы линейных алгебраических уравнений методом Гаусса удобно выписать расширенную матрицу системы и все преобразования выполнять над строками и столбцами расширенной матрицы.
Рассмотрим примеры решения систем линейных алгебраических уравнений методом Гаусса.
Пример 1.

Решение.
Выпишем расширенную матрицу системы:
 ~
(не меняя первую строку, вычтем из второй
~
(не меняя первую строку, вычтем из второй
строки первую, из третьей вычтем первую строку, умноженную
на
3) ~
 ~ (первую и вторую строки не меняем,
~ (первую и вторую строки не меняем,
а
из третьей вычтем вторую, умноженную
на 4) ~
 .
.
Получили матрицу А треугольного вида, причем на диагонали элементы отличны от нуля. Следовательно, ранг матрицы А равен 3, ранг расширенной матрицы также равен 3, и по теореме Кронекера-Капелли исходная система совместна, причем имеет единственное решение. Получим это решение.
Согласно последней матрице исходную систему можно записать в виде:

Из
последнего уравнения имеем, что
 =
–1. Подставляя
=
–1. Подставляя
 во
второе уравнение, получим
во
второе уравнение, получим
 Подставляя
Подставляя
 и
и

в
первое уравнение, получим

Ответ:

Пример 2.

Решение.
Выпишем расширенную матрицу системы:
 ~
(первую и четвертую строки не меняем,
из
~
(первую и четвертую строки не меняем,
из
второй строки вычтем первую, умноженную на 3, из третьей строки вычтем
первую)
~
 ~ (первую и вторую строки не меняем, из
третьей строки вычтем вторую, умноженную
на
~ (первую и вторую строки не меняем, из
третьей строки вычтем вторую, умноженную
на
 ,
а из четвертой вычтем вторую, умноженную
на
,
а из четвертой вычтем вторую, умноженную
на
 )
~
)
~
 ~
~
~ (первую, вторую и третью строки не меняем, к четвертой строке
прибавим
третью) ~
 .
.
В итоге получили трапециевидную матрицу А. Следовательно, если бы последняя строка расширенной матрицы была нулевой, то исходная система уравнений имела бы бесконечное множество решений.
Так
как она дает уравнение
 ,
которое не имеет решения, то исходная
система является несовместной, то есть
не имеет решений.
,
которое не имеет решения, то исходная
система является несовместной, то есть
не имеет решений.
