
- •Действия с матрицами: умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.
- •Определители 2-го и 3-го порядков. Свойства определителей.
- •Миноры и алгебраические дополнения. Вычисление определителей с помощью формул разложения.
- •Обратная матрица и ее вычисление.
- •Ранг матрицы. Вычисление ранга с помощью элементарных преобразований.
- •Системы линейных алгебраических уравнений. Матричный способ решения систем линейных алгебраических уравнений.
- •Теорема Кронекера-Капелли о совместности системы линейных алгебраических уравнений.
- •Формулы Крамера решения систем линейных алгебраических уравнений.
- •Метод Гаусса решения систем линейных алгебраических уравнений.
- •Скалярные и векторные величины. Линейные операции с векторами.
- •Понятие базиса на плоскости и в пространстве. Ортонормированные базисы на плоскости и в пространстве. Координаты вектора в базисе.
- •Скалярное произведение. Координатная форма скалярного произведения.
- •Векторное произведение. Координатная форма векторного произведения.
- •Смешанное произведение. Координатная форма смешанного произведения.
- •Уравнение прямой (на плоскости), уравнение плоскости, заданных точкой и нормальным вектором.
- •– Каноническое уравнение эллипса с центром в точке
- •Парабола и ее основные свойства.
- •Гипербола и ее основные свойства.
- •Прямые называются директрисами гиперболы. – левая директриса,
-
Скалярные и векторные величины. Линейные операции с векторами.
Вектором называется
направленный отрезок
 где точка А
– начало вектора, точка В
– конец вектора. Если начало и конец
вектора в явном виде не указаны, то
вектор будем обозначать
где точка А
– начало вектора, точка В
– конец вектора. Если начало и конец
вектора в явном виде не указаны, то
вектор будем обозначать
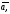
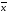 и т. д.
и т. д.
Вектор, у которого
начало и конец совпадают, называется
нулевым
вектором и обозначается
 .
.
Длиной
(модулем)
вектора называется длина его направленного
отрезка и обозначается
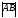 ,
,
 .
.
Вектор, длина которого равна единице, называется единичным или ортом.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.
Два вектора
 и
и
 называются равными
называются равными
 ,
если они коллинеарны, имеют одинаковую
длину и одинаковое направление.
,
если они коллинеарны, имеют одинаковую
длину и одинаковое направление.
Свободный вектор – это вектор, который можно переносить параллельно самому себе в любую точку пространства (плоскости).
Произведением
вектора
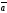 на
число
на
число
 называется вектор
называется вектор
 ,
длина которого
,
длина которого
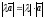 ;
направление совпадает с направлением
вектора
;
направление совпадает с направлением
вектора
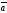 ,
если
,
если
 ,
и противоположно ему, если
,
и противоположно ему, если
 .
.
Суммой двух
векторов
 и
и
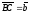 называется вектор
называется вектор
 (рис. 1) и обозначается
(рис. 1) и обозначается
 .
.

Разностью двух
векторов
 и
и
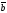 называется вектор
называется вектор
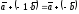 и обозначается
и обозначается
 (рис. 2).
(рис. 2).
Векторы, лежащие в одной плоскости или на параллельных плоскостях, называются компланарными.
Декартовой
прямоугольной системой координат в
пространстве
(прямо-угольной)
называется совокупность трех упорядоченных
взаимно перпендикулярных осей координат
ОХ, ОY,
OZ с
общим
началом в точке О.
Орты координатных осей ОХ,
ОY,
ОZ
обозначают
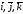 соответственно. Векторы
соответственно. Векторы
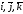 образуют декартовый прямоугольный
базис в пространстве.
образуют декартовый прямоугольный
базис в пространстве.
-
Понятие базиса на плоскости и в пространстве. Ортонормированные базисы на плоскости и в пространстве. Координаты вектора в базисе.
Базисом на
плоскости
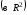 называется упорядоченная пара любых
некомпланарных векторов этой плоскости.
называется упорядоченная пара любых
некомпланарных векторов этой плоскости.
Базисом в
пространстве
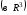 называется упорядоченная тройка любых
некомпланарных векторов.
называется упорядоченная тройка любых
некомпланарных векторов.
Векторы
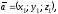
 ,
,
 в пространстве образуют базис тогда и
только тогда, когда определитель матрицы,
составленной из их координат,
в пространстве образуют базис тогда и
только тогда, когда определитель матрицы,
составленной из их координат,
не равен нулю:
 .
.
Если
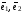 – базис на плоскости, то любой вектор
– базис на плоскости, то любой вектор
 этой плоскости единственным образом
представляется в виде линейной комбинации
векторов
этой плоскости единственным образом
представляется в виде линейной комбинации
векторов
 т. е.
т. е.
 .
.
Числа
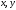 называют координатами
вектора
называют координатами
вектора
 в базисе
в базисе
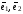 и записывают
и записывают
 .
.
Если
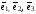 – базис в пространстве, то любой вектор
– базис в пространстве, то любой вектор
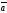 единственным обра-зом представляется
в виде линейной комбинации векторов
единственным обра-зом представляется
в виде линейной комбинации векторов
 ,
т. е.
,
т. е.
 .
Числа
.
Числа
 называют координатами
вектора
называют координатами
вектора
 в базисе
в базисе
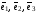 и записывают
и записывают
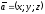 .
.
Координатами точки
М
в заданной системе координат называют
координаты ее радиус-вектора
 .
В этом случае пишут
.
В этом случае пишут
 или
или

Любой вектор
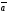 в пространстве единственным образом
представляется в виде линейной комбинации
векторов
в пространстве единственным образом
представляется в виде линейной комбинации
векторов
 т. е.
т. е.
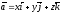 .
Числа
.
Числа
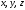 называют декартовыми
прямоугольными координатами вектора
называют декартовыми
прямоугольными координатами вектора
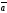 и записывают
и записывают
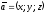 .
.
Линейные операции
над векторами в координатной форме:
пусть
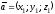 ,
,
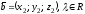 ,
тогда
,
тогда
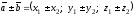 ,
,
 .
.
Длина вектора
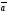 вычисляется по формуле
вычисляется по формуле
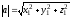 .
(2.1)
.
(2.1)
Если вектор
 задан координатами точек
задан координатами точек
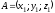 и
и
 ,
то
,
то
 .
.
