
- •Действия с матрицами: умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.
- •Определители 2-го и 3-го порядков. Свойства определителей.
- •Миноры и алгебраические дополнения. Вычисление определителей с помощью формул разложения.
- •Обратная матрица и ее вычисление.
- •Ранг матрицы. Вычисление ранга с помощью элементарных преобразований.
- •Системы линейных алгебраических уравнений. Матричный способ решения систем линейных алгебраических уравнений.
- •Теорема Кронекера-Капелли о совместности системы линейных алгебраических уравнений.
- •Формулы Крамера решения систем линейных алгебраических уравнений.
- •Метод Гаусса решения систем линейных алгебраических уравнений.
- •Скалярные и векторные величины. Линейные операции с векторами.
- •Понятие базиса на плоскости и в пространстве. Ортонормированные базисы на плоскости и в пространстве. Координаты вектора в базисе.
- •Скалярное произведение. Координатная форма скалярного произведения.
- •Векторное произведение. Координатная форма векторного произведения.
- •Смешанное произведение. Координатная форма смешанного произведения.
- •Уравнение прямой (на плоскости), уравнение плоскости, заданных точкой и нормальным вектором.
- •– Каноническое уравнение эллипса с центром в точке
- •Парабола и ее основные свойства.
- •Гипербола и ее основные свойства.
- •Прямые называются директрисами гиперболы. – левая директриса,
-
Теорема Кронекера-Капелли о совместности системы линейных алгебраических уравнений.
Теорема Кронекера-Капелли.
Для того, чтобы система линейных алгебраических уравнений была совместной (то есть имела решение), необходимо и достаточно, чтобы ранг исходной матрицы системы совпадал с рангом расширенной матрицы, то есть r(A) = r(С).
-
если r(A) = r(С)= n, где n – число неизвестных системы, то данная система имеет единственное решение;
-
если r(A) = r(С) = k < n, то система имеет бесконечное множество решений;
-
если r(A) ≠ r(С), то система несовместна, то есть не имеет решений.
Если число неизвестных больше числа уравнений, то система либо не имеет решений, либо имеет их бесконечное множество (если r(A) = r(С) = =k < n.)
Пример. Исследовать систему уравнений на совместность

Решение.
Запишем матрицу системы А и определим ее ранг:
 .
.
Так как матрица А имеет порядок 34, то r (A) ≤ 3. Существует
4 различных минора третьего порядка:
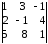 ,
,
 ,
,
 ,
,
 .
.
Легко проверить, что все эти миноры равны нулю. Например:
 =
= =6ּ
=6ּ
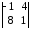 +11ּ
+11ּ


Так как минор
второго порядка
 ,то
r
(A)
= 2.
,то
r
(A)
= 2.
Рассмотрим
расширенную матрицу
 .
Так как минор третьего порядка
.
Так как минор третьего порядка
 =
=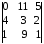 =11ּ
=11ּ
 +5ּ
+5ּ
 =
=
= –11ּ2+5ּ33= –22+165=143 ≠ 0, то r(С)=3.
Следовательно, r (A) ≠ r (С), и по теореме Кронекера-Капелли система несовместна, то есть не имеет решений.
Действительно,
если первое уравнение системы умножить
на 3 и сложить со вторым уравнением, то
получим уравнение
 .
Левая часть этого уравнения совпадает
с левой частью третьего уравнения
системы, а правые части у них разные.
Следовательно, система не имеет решений.
.
Левая часть этого уравнения совпадает
с левой частью третьего уравнения
системы, а правые части у них разные.
Следовательно, система не имеет решений.
Пример. Исследовать на совместность и решить систему линейных алгебраических уравнений
 (2)
(2)
-
с помощью формул Крамера;
-
матричным методом.
Решение.
Запишем матрицу А системы уравнений и определим ее ранг:
 .
.
Так как

 (третья
строка определителя является суммой
первых двух строк), то r(A)<
3. Рассмотрим какой-либо минор
(третья
строка определителя является суммой
первых двух строк), то r(A)<
3. Рассмотрим какой-либо минор
второго порядка:

Рассмотрим
расширенную матрицу системы:
 .
.
Найдем ее ранг. Существуют 4 различных минора третьего порядка:
 ,
,
 ,
,
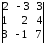 ,
,
 .
.
Легко проверить,
что все эти миноры равны нулю (в каждом
из них третья строка есть сумма первых
двух строк). Поэтому r
(С) < 3. Так как выше рассмотренный минор
второго порядка
 принадлежит и матрице С, то
принадлежит и матрице С, то
 ,
и по теореме Кронекера-Капелли исходная
система уравнений совместна (r(A)
= r(С)).
Но, так как r(A)
= r
(С) = 2 < 3, где 3 – число неизвестных
системы уравнений, то исходная система
имеет бесконечное множество решений.
,
и по теореме Кронекера-Капелли исходная
система уравнений совместна (r(A)
= r(С)).
Но, так как r(A)
= r
(С) = 2 < 3, где 3 – число неизвестных
системы уравнений, то исходная система
имеет бесконечное множество решений.
Отличный от нуля
минор второго порядка
 состоит из коэффициентов, стоящих при
неизвестных
состоит из коэффициентов, стоящих при
неизвестных
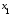 и
и
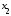 первого и второго уравнения. Следовательно,
первая и вторая строка матрицы А линейно
независимы, а третья выражается через
них (является их суммой). Поэтому третье
уравнение системы можно отбросить.
первого и второго уравнения. Следовательно,
первая и вторая строка матрицы А линейно
независимы, а третья выражается через
них (является их суммой). Поэтому третье
уравнение системы можно отбросить.
Так как элементы
данного минора – это коэффициенты при
 и
и
 ,
то эти переменные будут базисными, а
,
то эти переменные будут базисными, а
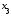 «лишней» (свободной), поэтому перенесем
ее в правые части уравнений. В итоге
получим систему:
«лишней» (свободной), поэтому перенесем
ее в правые части уравнений. В итоге
получим систему:
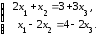 (3)
(3)
В данном случае
определитель матрицы системы
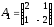 не равен нулю. Следовательно, существует
обратная матрица
не равен нулю. Следовательно, существует
обратная матрица
 ,
и мы можем решить систему уравнений
матричным методом и по формулам Крамера.
,
и мы можем решить систему уравнений
матричным методом и по формулам Крамера.
