Высшая математика.

1. Действия с матрицами: умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.

Матрицей размера 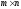называется прямоугольная таблица чисел, содержащая т строк и п столбцов.

Матрица, у которой число строк равно числу столбцов 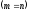, называется квадратной матрицей порядка п. Нулевой называется матрица, все элементы которой равны нулю. Ее обозначают буквой О.

Диагональной называется квадратная матрица, у которой все элементы, стоящие не на главной диагонали, равны нулю. Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной и обозначается буквой Е.

Для матриц одинакового размера вводятся операции сложения и вычитания.

Для того чтобы сложить две матрицы 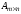и , достаточно сложить их соответствующие элементы. Операция обозначается .

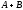Для того чтобы из матрицы 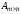вычесть матрицу , достаточно из каждого элемента матрицы А вычесть соответствующие элементы матрицы В. Операция обозначается .

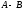Для того чтобы матрицу 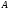умножить на число , достаточно все элементы матрицы умножить на число . Операция обозначается или .

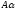Произведение матрицы 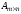на матрицу 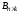вводится только для согласованных матриц, т. е. число столбцов матрицы 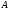должно равняться числу строк матрицы 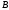(число п). Операция обозначается .

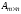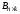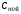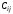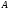Произведением матриц и называется такая матрица , каждый элемент которой равен сумме произведений элементов i-й строки матрицы на соответствующие элементы j-го столбца матрицы .

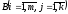Произведение матриц не обладает свойством коммутативности, т. е. не всегда 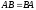, даже если произведения имеют смысл.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Ее обозначают .

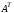2. Определители 2-го и 3-го порядков. Свойства определителей.

Определителем второго порядка матрицы 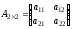называется число, равное произведению элементов главной диагонали минус произведение элементов побочной диагонали, т. е.

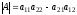. (1.1)

Определителем третьего порядка матрицы

называется число, вычисляемое по формуле

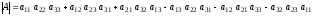. (1.2)

Чтобы составить выражение (1.2), используют символическое правило треугольников (правило Саррюса):

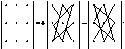
Основные свойства определителей

1. Определитель матрицы не изменяется при ее транспонировании, т. е.

2. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

3. Общий множитель всех элементов какой-либо строки (столбца) матрицы можно вынести за знак ее определителя.

4. Определитель матрицы с нулевой строкой (столбцом) равен нулю.

5. Определитель матрицы не изменится, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

6. Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.

7. Определитель произведения двух квадратных матриц равен произведению их определителей, т. е. .
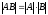