2. Формулы крамера

Рассмотрим еще один метод решения системы (1). Пусть, как и ранее, n=m.

Тогда из формулы (3) имеем:

Х=В

==

. (4)

В формуле (4) =detA– главный определитель системы (1),

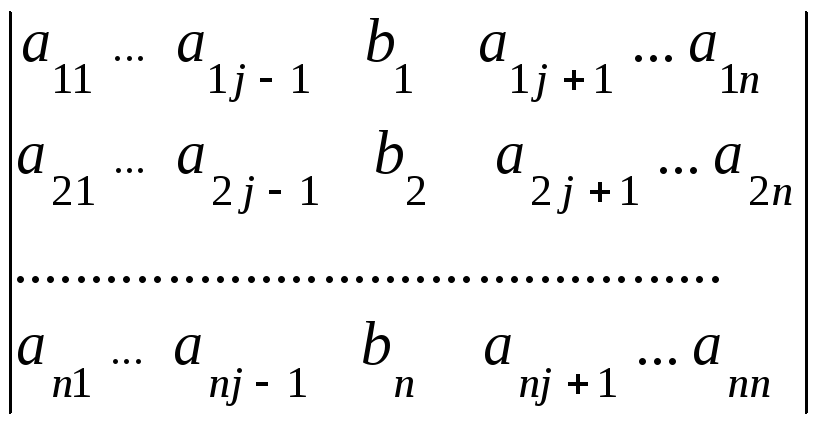= (разлагаем по j-му столбцу)=

= ;, – побочные определители системы (1).

Они получаются из главного определителя заменой соответствующего j-го столбца столбцом свободных членов. Формулы (4) называютсяформулами Крамера.

Алгоритм решения систем линейных алгебраических уравнений с помощью формул Крамера

1. Для матрицы А системы уравнений вычислить ее главный определитель =detA.

2. Последовательно, заменяя каждый столбец матрицы А столбцом свободных членов, получить побочные определители ,.

3. а) Если ≠ 0, то по формулам (4) определить единственное решение системы (1):,, ….,.

б) Если =0, а хотя бы один из побочных определителей≠0, то исходная система (1) несовместна, то есть не имеет решений.

в) Если == 0,, то исходная система (1) имеет бесконечное множество решений.

Пример.Решить систему линейных алгебраических уравнений с помощью формул Крамера

Решение.

1. Матрица А имеет вид: А = ,detA==5 ≠ 0,

Следовательно, система имеет единственное решение.

2. Найдем побочные определители системы:

=10ּ+(–1)ּ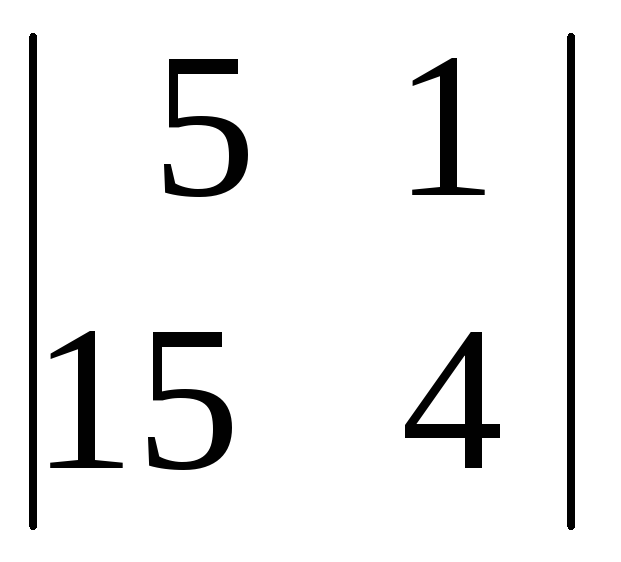=10ּ5+5=55;

=3ּ+10ּ=3ּ5–10ּ(–10)=115;

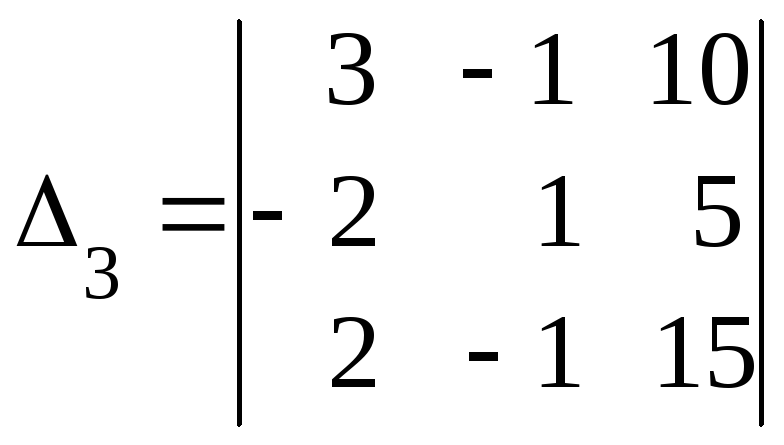=( упростим, сложив первую строку со второй и

третью со второй)= =20ּ =20.

3. Найдем решение системы по формулам (4):

, ,.

Ответ:

Естественно, что получен такой же ответ, как и при решении системы уравнений матричным способом (см. выше).

3. Совместность систем лау. Ранг матрицы. Теорема кронекера-капелли

В предыдущем вопросе было дано определение совместной системы линейных алгебраических уравнений. Исследовать же систему на совместность – это, значит, определить, имеет ли система какое-либо решение (единственное или бесконечное множество).

Введем новые понятия из теории матриц.

Пусть дана матрица общего вида порядка mn:

А=.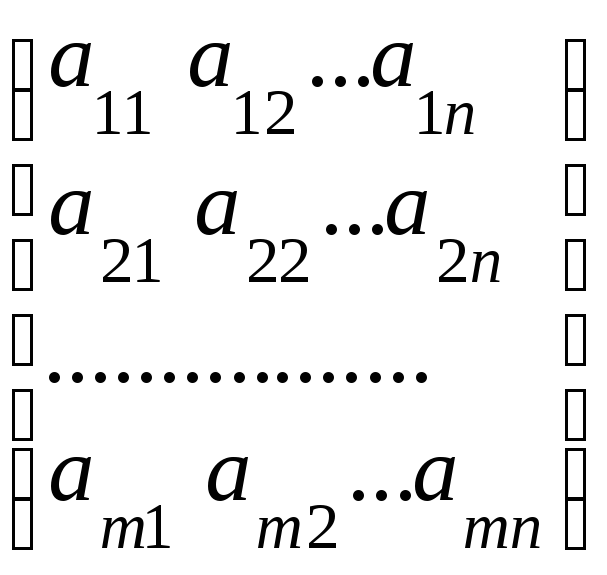

Обозначим строки матрицы через ,, …,:

= ,=, …,=.

Пусть

=,,

=.

Тогда сумма ++…+,, будет называтьсялинейной комбинацией строк() матрицы А.

Если существуют числа , такие что=++…+++...+, то говорят, что строкавыражается через остальные строки,, …,,, …,. Строки,, …,называютсялинейно зависимыми, если существуют числа

, не все одновременно равные нулю, что ++…+=0, где 0=(0 0 …0). Если же данное равенство выполняется лишь когда все числа=0,, то говорят, что строки,,линейно независимы. Заметим, что, если строки линейно зависимы, то, по крайней мере, одна из них выражается через остальные. Если же строки линейно независимы, то ни одна строка не выражается через остальные. Аналогично вводится понятие линейной зависимости и независимости столбцов.

Введем понятие ранга матрицы.

Рангом r(A)матрицы А называется максимальный порядок ее миноров, отличных от нуля. Миноромk-го порядка матрицы А называется определительk-го порядка, построенный из элементов матрицы А, находящихся на пересеченииkстрок и k столбцов матрицы А.Базисным минором матрицы называется всякий отличный от нуля минор, порядок которого равен рангу данной матрицы.

Пример.Определить ранг матрицы

.

Решение.

Матрица А имеет порядок 3х4, следовательно, ранг матрицы .

Для определения ранга вначале найдем все возможные миноры третьего порядка: если хотя бы один из них отличен от нуля, значит ранг матрицы А равен трем. Всего имеем четыре минора третьего порядка:

, ,,.

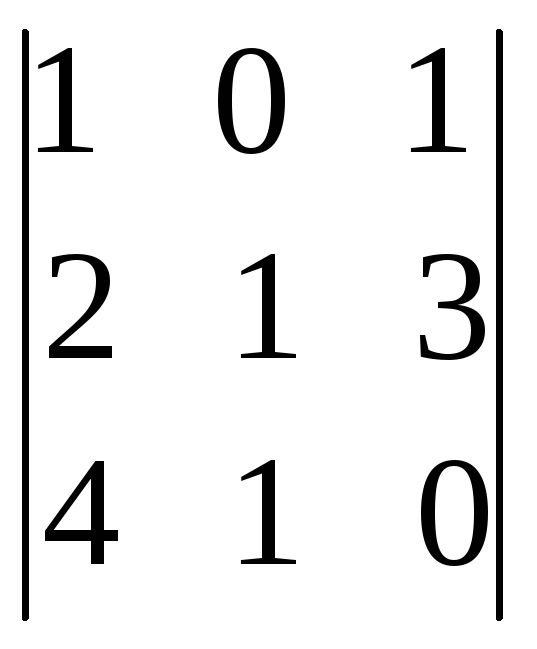Так как достаточно найти среди них хотя бы один отличный от нуля, то выберем тот минор, который содержит большее количество нулевых элементов:

=1ּ

Данный минор будет являться базисным для исходной матрицы.

Если бы все приведенные в примере миноры третьего порядка оказались равными нулю, то это привело бы к рассмотрению миноров второго порядка. Естественно, в этом случае ранг матрицы был бы ниже трех.

Матрицы А и В называются эквивалентными (А~В), если одна из них получается из другой с помощью элементарных преобразований. К элементарным преобразованиям относят:

1. перестановка местами любых двух строк (столбцов) матрицы;

2. умножение каждого элемента строки (столбца) на один и тот же множитель λ ≠ 0;

3. прибавление (вычитание) к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на один и тот же множитель.

Ранги эквивалентных матриц совпадают, то есть ранг матрицы не меняется, если к матрице применить элементарные преобразования 1-3. На этом основан один из методов нахождения ранга матрицы – метод нулей и единиц. Он заключается в том, что при помощи элементарных преобразований матрица сводится к эквивалентной, состоящей только из нулей и единиц. Ранг матрицы будет равен числу единиц в эквивалентной матрице.

Пример.Найти ранг матрицы А методом нулей и единиц (смотри предыдущий пример)

.

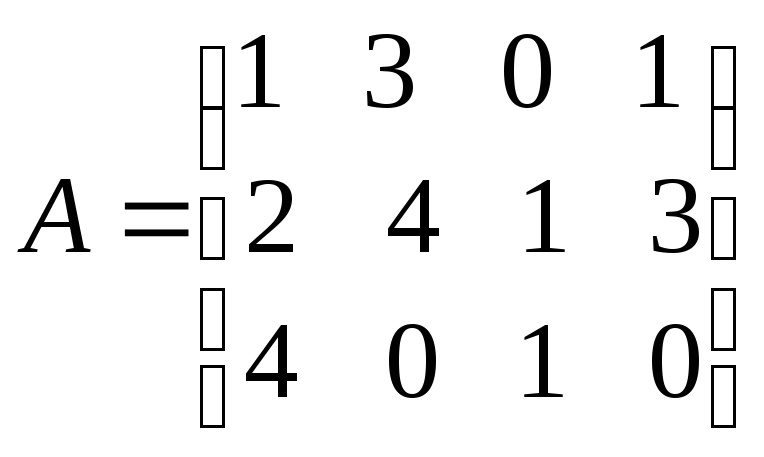Решение.

~ (вычтем из второй строки первую) ~

~ (вычтем из первого и второго столбца третий) ~~

~ (вычтем из второго столбца первый, умноженный на 3)

~~

~ (разделим второй столбец на (-10) ) ~ ~ (вычтем из первого столбца второй, умноженный на 3, и из третьего вычтем второй)

~ ~ (вычтем из четвертого столбца третий, умноженный на 2) ~

~~ (вычтем из первого столбца четвертый) ~

~, так как получили три единицы.

Учитывая, что единицы находятся на пересечении первой, второй, третьей строк и второго, третьего и четвертого столбцов, и так как в ходе преобразований мы не меняли местами строки и столбцы, то в качестве базисного минора исходной матрицы А возьмем минор, получаемый из указанных строк и столбцов:

= 0.

Ранг матрицы равен нулю тогда и только тогда, когда А – нулевая матрица. Если хотя бы один элемент матрицы А не равен нулю, то ранг матрицы больше нуля. Таким образом, ранг является еще одной важной характеристикой матрицы. Имеют место следующие утверждения:

1. если ранг матрицы А равен k, то существует ровноkлинейно-независимых строк (столбцов), от которых линейно зависят все остальные строки (столбцы), то есть все остальные строки выражаются через этиkлинейно-независимых строк;

2. максимальное число линейно-независимых строк матрицы совпадает с максимальным числом линейно-независимых столбцов и равно рангу матрицы.

Пусть дана система mлинейных алгебраических уравнений сnнеизвестными:

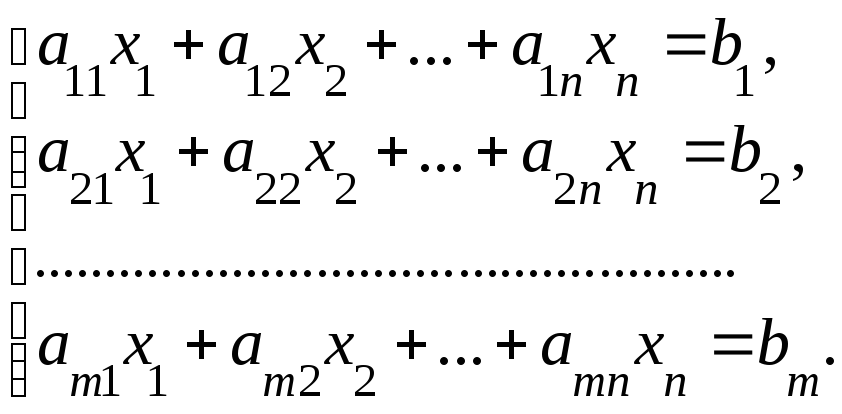(1)

Дополним матрицу А системы (1) столбцом свободных членов.

В итоге будем иметь так называемую расширенную матрицу системы (1):

.

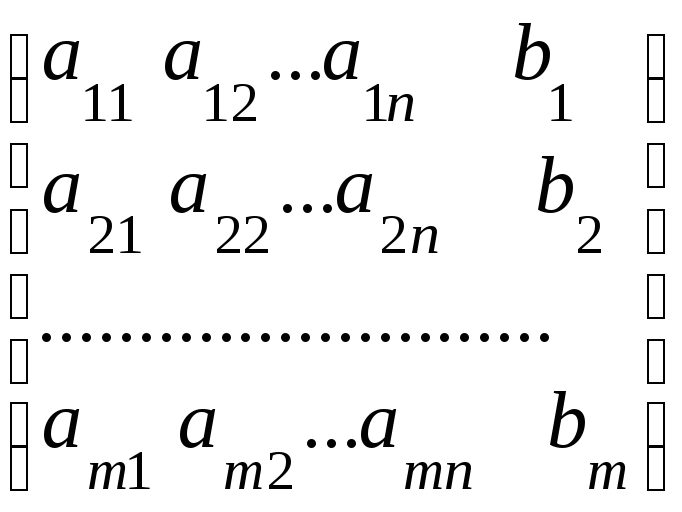Обозначим через r(A) иr(С) ранги матриц А и С соответственно. Сформулируем теорему Кронекера-Капелли, которая определяет условия, при которых система (1) имеет или не имеет решения.

Теорема Кронекера-Капелли.

Для того, чтобы система линейных алгебраических уравнений была совместной (то есть имела решение), необходимо и достаточно, чтобы ранг исходной матрицы системы совпадал с рангом расширенной матрицы, то есть r(A) =r(С).

1. если r(A) =r(С)=n, гдеn– число неизвестных системы, то данная система имеет единственное решение;

2. если r(A) =r(С) = k <n, то система имеет бесконечное множество решений;

3. если r(A) ≠r(С), то система несовместна, то есть не имеет решений.

Если число неизвестных больше числа уравнений, то система либо не имеет решений, либо имеет их бесконечное множество (если r(A) =r(С) = =k <n.)

Пример.Исследовать систему уравнений на совместность

Решение.

Запишем матрицу системы А и определим ее ранг:

.

Так как матрица А имеет порядок 34, тоr(A) ≤ 3. Существует

4 различных минора третьего порядка:

, ,,.

Легко проверить, что все эти миноры равны нулю. Например:

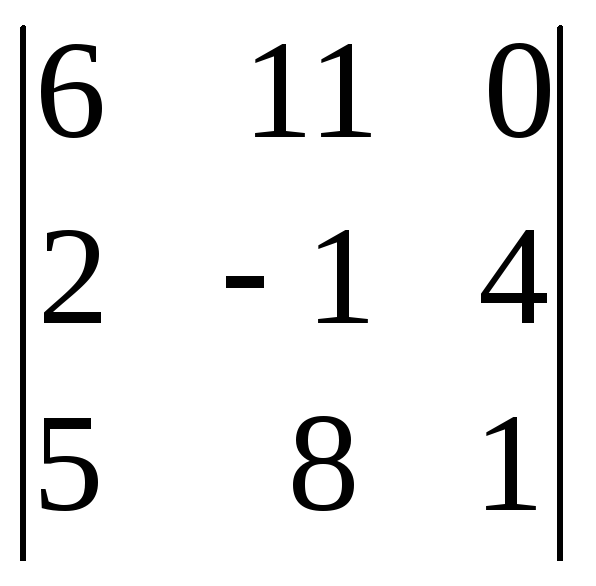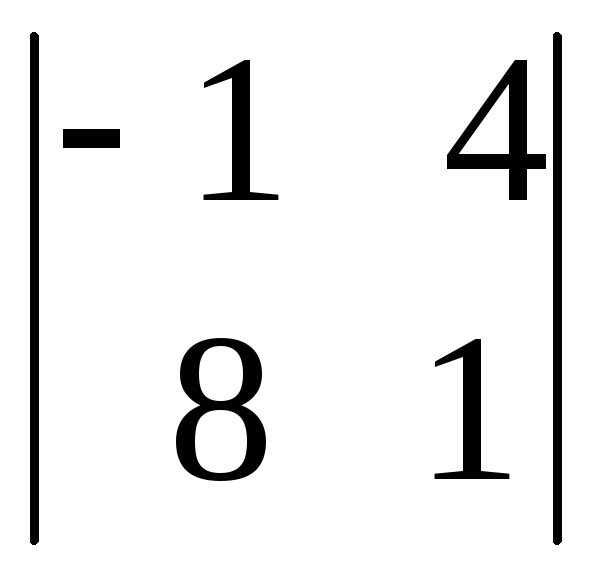==6ּ+11ּ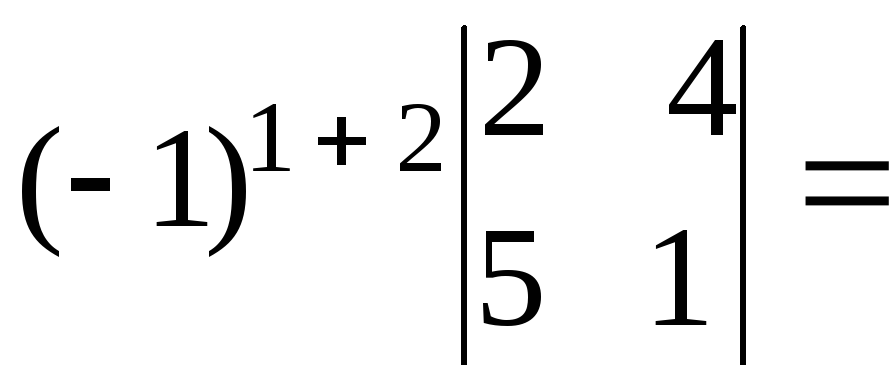

Так как минор второго порядка ,тоr(A) = 2.

Рассмотрим расширенную матрицу . Так как минор третьего порядка

==11ּ+5ּ=

= –11ּ2+5ּ33= –22+165=143 ≠ 0, то r(С)=3.

Следовательно, r(A) ≠r(С), и по теореме Кронекера-Капелли система несовместна, то есть не имеет решений.

Действительно, если первое уравнение системы умножить на 3 и сложить со вторым уравнением, то получим уравнение . Левая часть этого уравнения совпадает с левой частью третьего уравнения системы, а правые части у них разные. Следовательно, система не имеет решений.

Пример.Исследовать на совместность и решить систему линейных алгебраических уравнений

(2)

1. с помощью формул Крамера;

2. матричным методом.

Решение.

Запишем матрицу А системы уравнений и определим ее ранг:

.

Так как (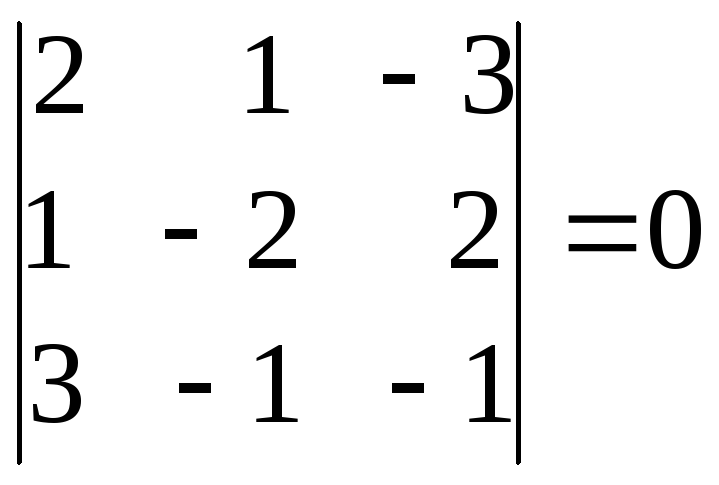третья строка определителя является суммой первых двух строк), тоr(A)< 3. Рассмотрим какой-либо минор

второго порядка:

Рассмотрим расширенную матрицу системы: .

Найдем ее ранг. Существуют 4 различных минора третьего порядка:

, ,,.

Легко проверить, что все эти миноры равны нулю (в каждом из них третья строка есть сумма первых двух строк). Поэтому r(С) < 3. Так как выше рассмотренный минор второго порядкапринадлежит и матрице С, то

, и по теореме Кронекера-Капелли исходная система уравнений совместна (r(A) =r(С)). Но, так какr(A) =r(С) = 2 < 3, где 3 – число неизвестных системы уравнений, то исходная система имеет бесконечное множество решений.

Отличный от нуля минор второго порядка состоит из коэффициентов, стоящих при неизвестныхипервого и второго уравнения. Следовательно, первая и вторая строка матрицы А линейно независимы, а третья выражается через них (является их суммой). Поэтому третье уравнение системы можно отбросить.

Так как элементы данного минора – это коэффициенты при и, то эти переменные будут базисными, а«лишней» (свободной), поэтому перенесем ее в правые части уравнений. В итоге получим систему:

(3)

В данном случае определитель матрицы системы не равен нулю. Следовательно, существует обратная матрица, и мы можем решить систему уравнений матричным методом и по формулам Крамера.

1. решим систему (3) по формулам Крамера.

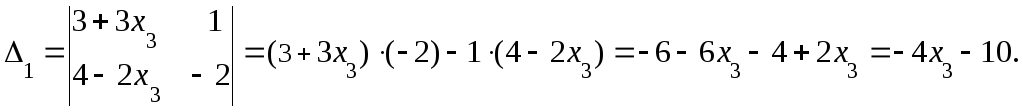
Заметим, что для нахождения побочных определителей имы использовали правую часть уравнений системы (3), содержащую свободную переменную. По формулам Крамера получаем:

, .

Обозначив получим решение исходной системы уравнений (2):

(4)

Задавая произвольные значения переменной t, мы будем получать каждый раз новое решений системы (2), то есть исходная система линейных алгебраических уравнений имеет бесконечное множество решений.

2. Решим систему (3) матричным методом.

существует обратная матрица .

Найдем ее.

Составим матрицу из алгебраических дополнений элементов матрицы

==.

Транспонируя матрицу , получим присоединенную матрицу

.

Найдем обратную матрицу

==.

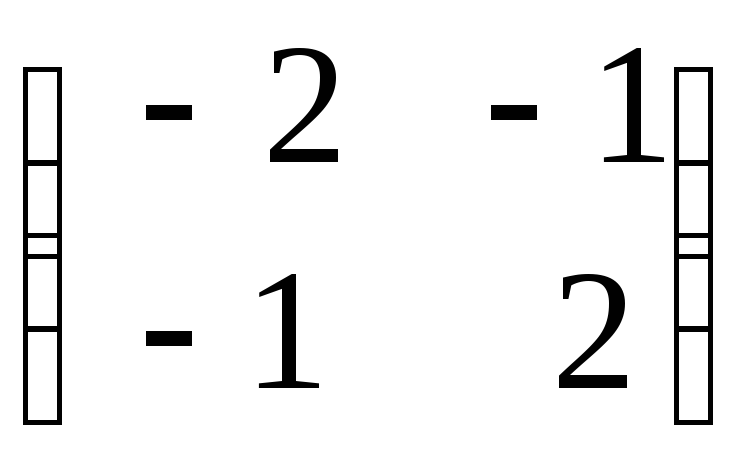Проверим правильность нахождения

=ּ=

=, значит, матрица

построена верно (равенство А₁^-1  А₁ = Епроверить самостоятельно).

Найдем решение системы (3):

=ּ=ּ = =

==.

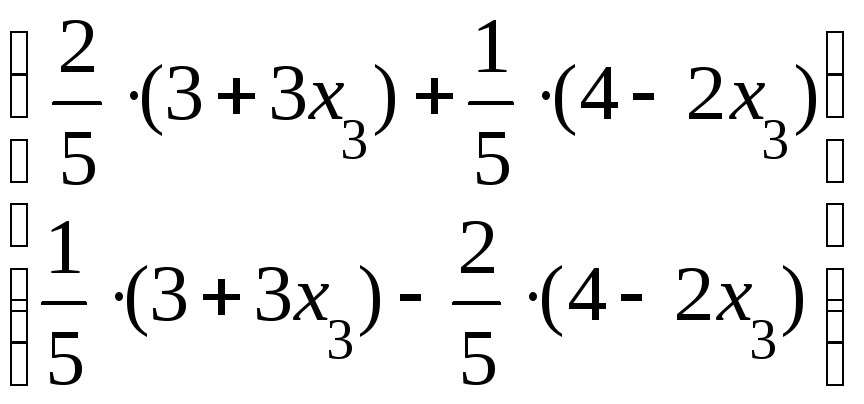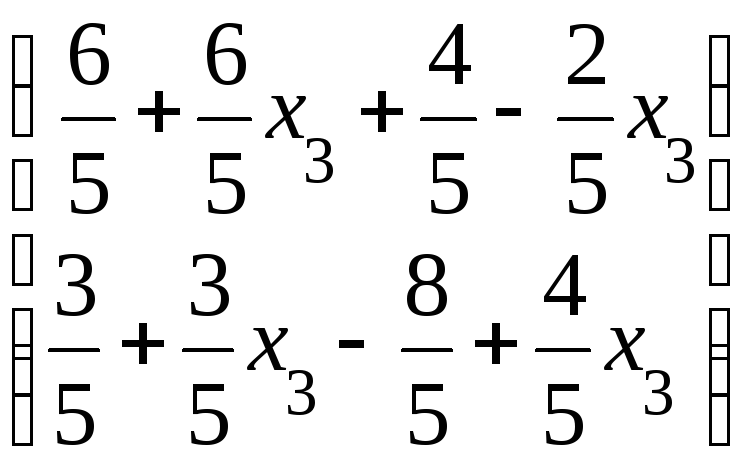Следовательно, обозначив получим решение исходной системы уравнений (2):

(5)

Заметим, что формулы (5) совпадают с формулами (4), что естественно, так как это решения одной и той же системы уравнений (2), полученные разными методами.

Анализируя данный пример, можно сделать вывод, что формулы Крамера и матричный метод можно применять для решения систем линейных алгебраических уравнений, для которых r(A) =r(С) <n. Алгоритм решения таких систем достаточно прост:

– система «укорачивается» до невырожденной,

– решается по формулам Крамера или матричным методом;

– свободной переменной или переменным (их может быть несколько) присваиваются произвольные значения .

В итоге «не укороченная» система имеет бесконечное множество решений.

Рассмотрим систему линейных алгебраических уравнений (1), когда правая часть равна нулю, то есть . Такая система уравнений называетсяоднородной. Так как в этом случае матрица А системы и расширенная матрица С этой же системы отличаются лишь тем, что в матрице С есть дополнительный нулевой столбец, тоr(A) =r(С), и по теореме Кронекера-Капелли однородная система всегда совместна, то есть всегда имеет решение: единственное или бесконечное множество. Если система имеет единственное решение, то оно называетсятривиальным.

Важно установить, когда однородная система уравнений имеет ненулевое решение. По теореме Кронекера-Капелли это будет в случае, если

r(A) =r(С) =k<n, то есть когда система имеет бесконечное множество решений. Если однородная система содержитnуравнений сnнеизвестными, то она будет иметь ненулевые решения тогда и только тогда, когда0. Иначе, если, то АХ=0Х=, то есть если определитель системы не равен нулю, то решение будет единственным – нулевое (тривиальное).

Пример.Исследовать на совместность и решить систему линейных алгебраических уравнений

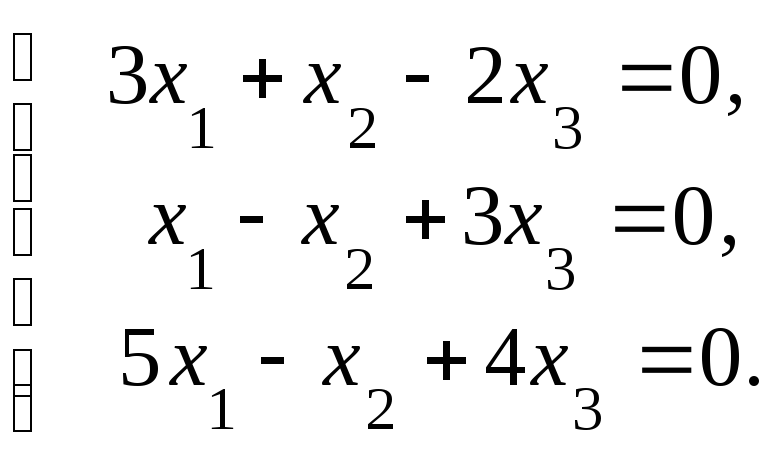
Решение.

detA===<3,

и система имеет бесконечное множество решений.

Найдем минор второго порядка отличный от нуля:.

Следовательно, первое и второе уравнения системы являются линейно-независимыми, а третье выражается через первые два, поэтому отбросим третье уравнение. Так как отличный от нуля минор состоит из коэффициентов при и, то эти переменные будут базисными, а– свободной. Получим систему из двух уравнений:

Сложив первое и второе уравнения, получим .

Отсюда ,

.

Таким образом, решением исходной системы будет:

Задавая произвольные значения переменной t, мы получаем каждый раз новое решение исходной системы, то есть система имеет бесконечное множество решений.