МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Частный институт управления и предпринимательства

Ю.В. Минченков

СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ

УРАВНЕНИЙ

Учебно-методическое пособие

Минск 2004

УДК

ББК

М-

Автор

Ю.В.Минченков, заведующий кафедрой высшей математики и статистики,

кандидат физико-математических наук, доцент

Обсуждено и одобрено на заседании

кафедры высшей математики и статистики,

протокол № 3 от 12.10 .2004г.

Рецензенты:

Т.А. Макаревич,кандидат физико-математических наук, доцент;

М.В. Чайковский, кандидат физико-математических наук, доцент

Минченков Ю.В.

М- Системы линейных алгебраических уравнений. Учеб.-метод. пособие / Ю.В. Минченков.-Мн.: Част. ин-т управ. и предпр., 2004.- с.

ISBN

Пособие включает лекции, задачи и упражнения, индивидуальные задания по теории систем линейных алгебраических уравнений.

Предназначено для студентов дневной и заочной форм обучения Частного института управления и предпринимательства.

УДК

ББК

ISBN



 Ю.В. Минченков, 2004

 Частный институт управления

и предпринимательства, 2004

ЛЕКЦИЯ. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ

УРАВНЕНИЙ

План

1. Понятие системы линейных алгебраических уравнений (ЛАУ). Решение системы ЛАУ матричным способом.

2. Формулы Крамера.

3. Совместность систем ЛАУ. Ранг матрицы. Теорема Кронекера-Капелли.

4. Метод Гаусса.

Ключевые понятия

Матричный способ решения системы ЛАУ.

Метод Гаусса.

Неоднородная система ЛАУ.

Несовместная система ЛАУ.

Однородная система ЛАУ.

Ранг матрицы.

Система ЛАУ.

Совместная система ЛАУ.

Теорема Кронекера-Капелли.

Формулы Крамера.

Эквивалентные матрицы.

1. ПОНЯТИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (ЛАУ). РЕШЕНИЕ СИСТЕМЫ ЛАУ

МАТРИЧНЫМ СПОСОБОМ

Системой m линейных алгебраических уравнений сnнеизвестныминазывается система вида

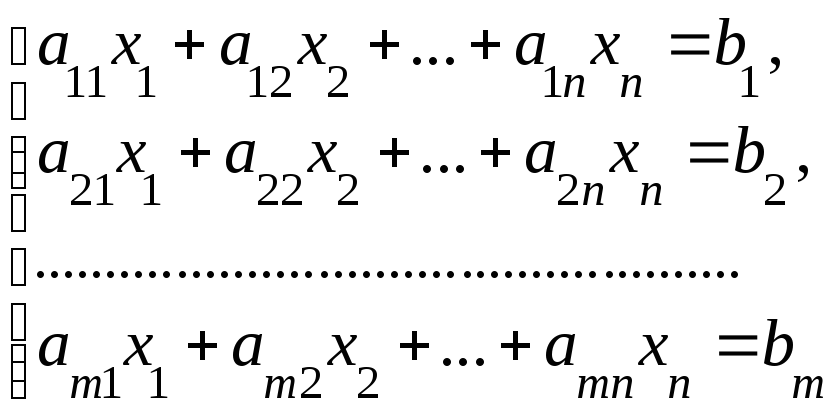(1)

Данная система может быть записана в матричном виде

АХ = В, (2)

где А = есть матрица системы (1), или матрица коэффициентов;

Х = 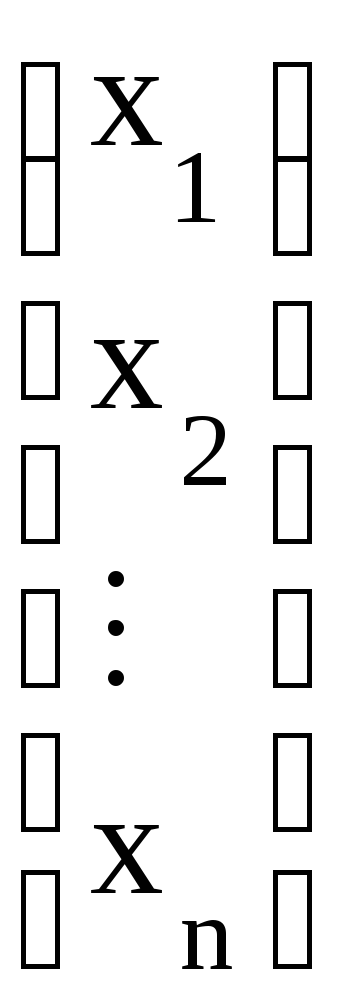есть матрица-столбец неизвестных; В =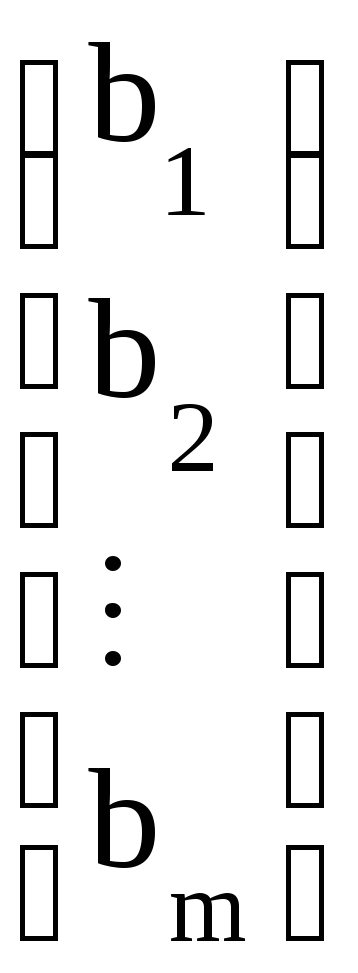есть матрица-

столбец свободных членов.

Если В = 0, то система (1) называется однородной, если же В ≠ 0, тонеоднородной.

Решением системы (1) называется всякая совокупность чисел, которая, будучи подставленной в систему, превращает каждое ее уравнение в тождество. Однако не каждая система линейных алгебраических уравнений имеет решение. Если не существует ни одной совокупности значений, удовлетворяющей заданным уравнениям системы, то система (1) называетсянесовместной. В противном случае, система (1) называетсясовместной. Совместная система может иметь или единственное решение, или бесконечное множество решений.

Пример 1.

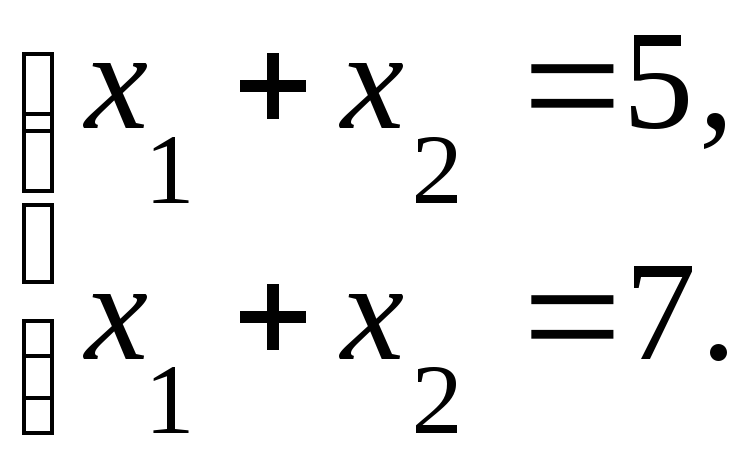–несовместная система (нет решений).

Пример 2.

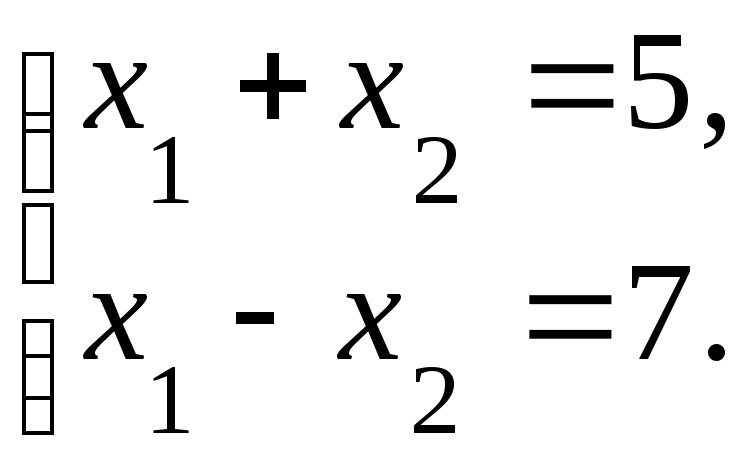–совместная система, имеющая единственное решение: .

Пример 3.

–совместная система, имеющая бесконечное множество решений: .

Рассмотрим матричный способрешения систем линейных алгебраических уравнений. Пусть в системе (1)m=nиdetA ≠ 0 (матрица невырожденная). Следовательно, существует обратная матрица. Умножим обе части равенства (2)слевана:АХ=ВЕХ=В, отсюда

Х =В. (3)

Формула (3) является матричной записью решения системы линейных алгебраических уравнений. Так как обратная матрица единственная, то система (1) (или, что то же самое, система (2)) имеет единственное решение.

Пример.Решить систему линейных алгебраических уравнений матричным способом.

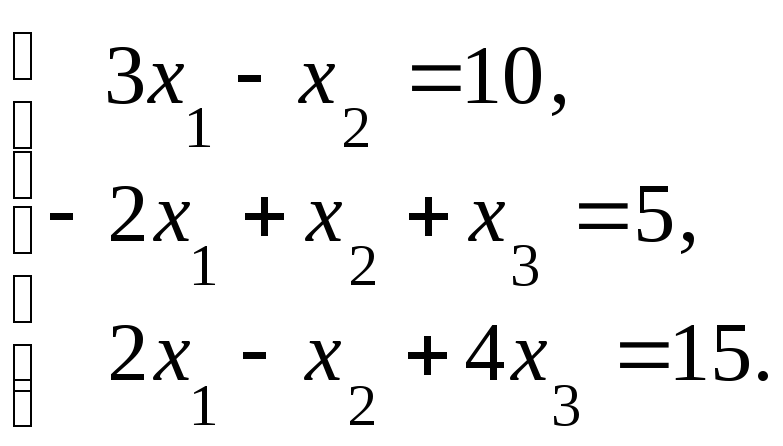
Решение.

1. Запишем основную матрицу системы : А=.

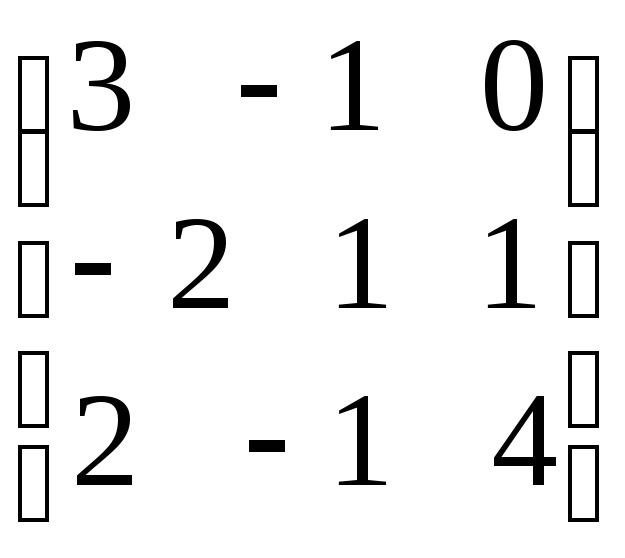2. Найдем определитель матрицы А:

detA = 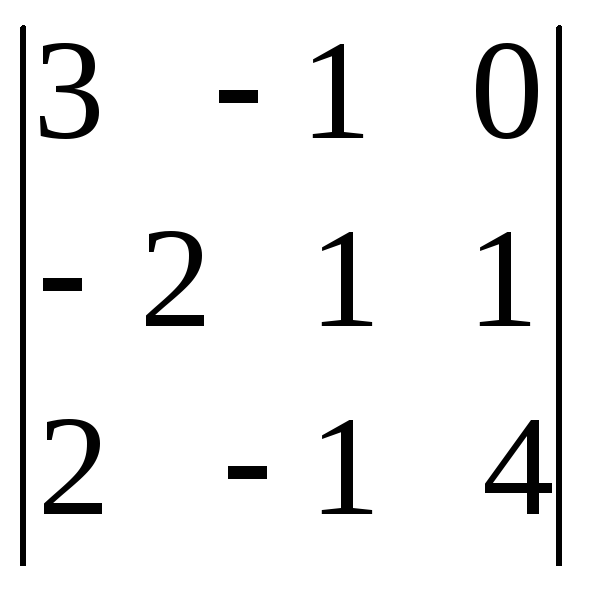=3ּ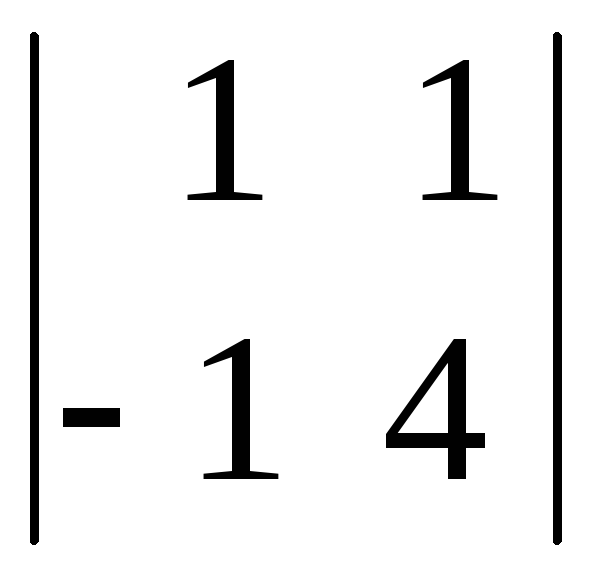+(–1)ּ= 3ּ(4+1)+(–8–2)=5.

Так как detA=5≠0, то существует обратная матрица, и, следовательно, исходная система имеет единственное решение Х=В.

3. Найдем обратную матрицу :

– составим матрицу из алгебраических дополнений элементов матрицы А

==;

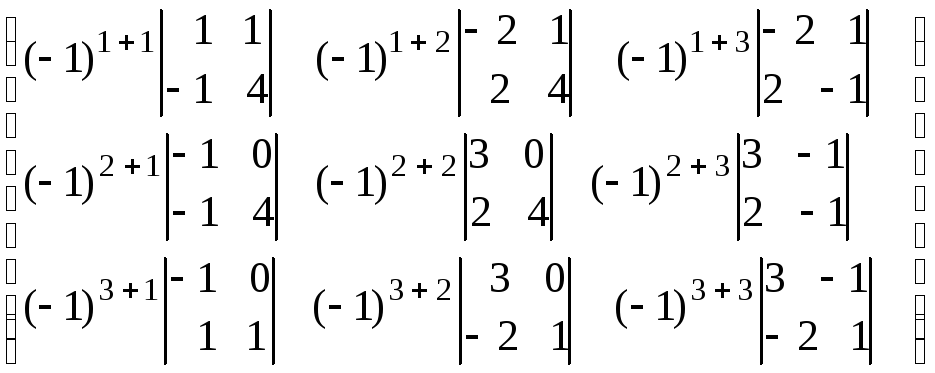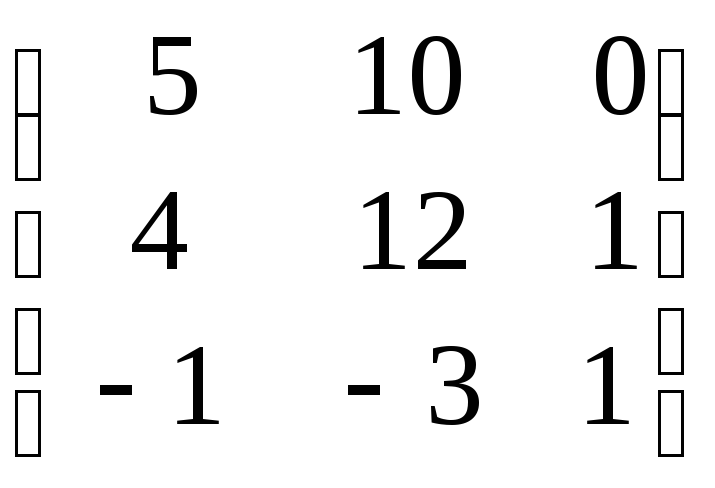транспонируя матрицу , получим присоединенную матрицу

;

найдем обратную матрицу

==.

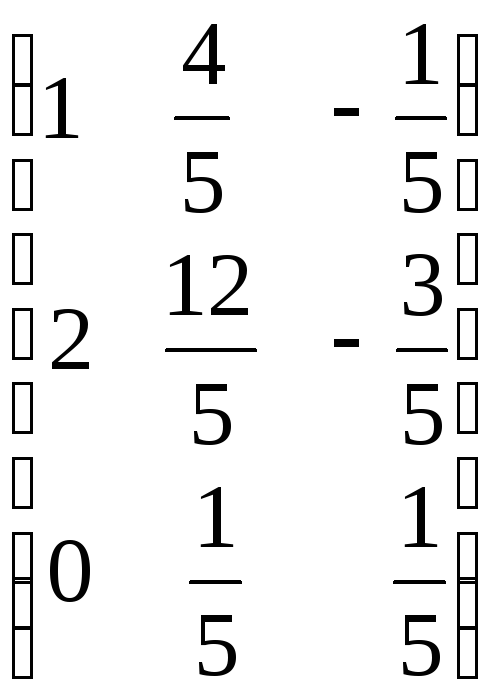4. Найдем решение исходной системы, учитывая, что В = :

Х = =В =ּ = =.

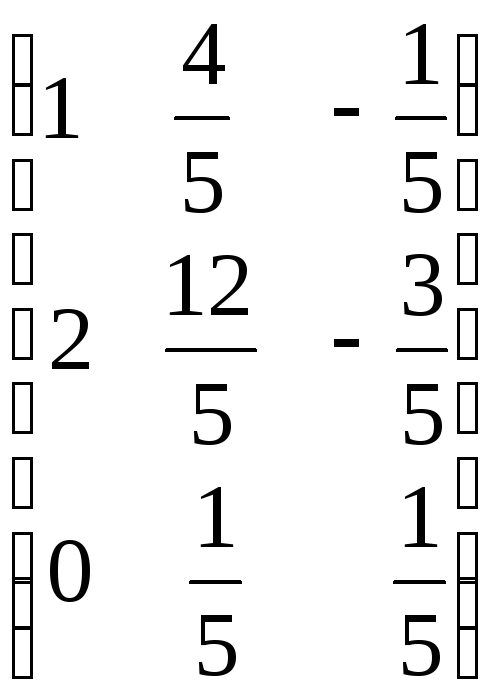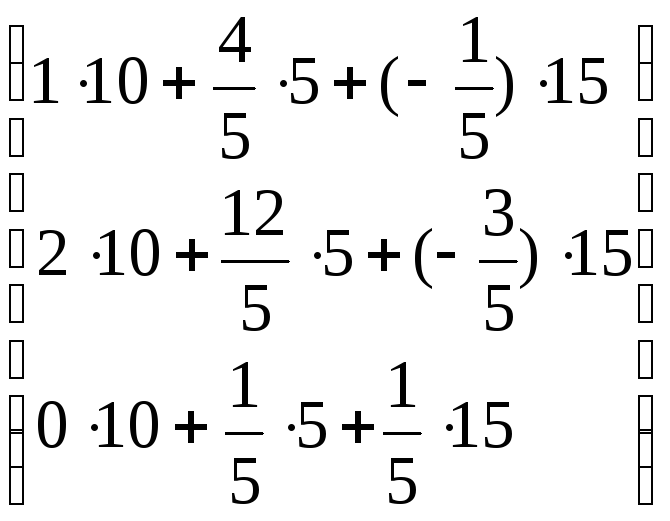Ответ: