
- •Программа
- •4. Общий объем дисциплины
- •5. Содержание дисциплины модуля
- •Тема 6 Прогнозирование и нелинейная регресия
- •5.3 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами
- •Примерная тематика курсовых проектов (работ) (не предусмотрена):
- •11.Программное обеспечение:
- •12. Материально-техническое обеспечение дисциплины:
- •13. Методические рекомендации по организации изучения дисциплины:
- •14. Методические рекомендации по организации изучения дисциплины
- •Алгоритм проведения научных дискуссий и круглых столов
- •15. Формы проведения контроля
- •1.Эконометрика- это:
- •2. Предметом эконометрики является:
- •3. Одному из методов эконометрики относится:
- •7.Пространственные выборки фиксируются:
- •25. Идентификация модели – это:
- •41. Достоверным называется такое событие, которое:
- •59. Обесценивание валюты влияет на деловую активность в экономической системе страны, реальный объем производства, занятость таким образом, что:
- •Вопросы для подготовки к зачету
- •Самостоятельная работа студентов Методические указания
- •Реферат Методические рекомендации
- •Описание объекта
- •Экономические показатели (факторы)
- •Для модели в абсолютных показателях
- •Для модели в относительных показателях
- •Выбор формы представления факторов
- •Анализ аномальных явлений
- •5. Анализ матрицы коэффициентов парных корреляций для абсолютных величин
- •А) Шаг первый
- •Б) Шаг второй.
- •7. Анализ матрицы коэффициентов парных корреляций для относительных величин
- •Примерная тематика рефератов
- •Контрольная работа Методические указания
- •Требования к оформлению
- •Методические указания к выполнению задания 1.
- •Задание 1. Разработка и анализ эконометрической модели
- •Методические указания по выполнению задания 2
- •Список литературы к задачам:
- •Контрольные задания для студентов заочной формы обучения
- •Тема 1. Предмет эконометрики.
- •Тема 2-3. Парная регрессия и корреляция в эконометрических исследованиях.
- •Тема 4. Многофакторный регрессионный анализ.
- •Варианты заданий.
- •2. Решение типовых задач.
- •3. Реализация типовых задач на компьютере.
- •Описательная статистика.
- •Тема 2..
- •Тема 3 Ресурсы современного мирового хозяйства.
- •Тема 4. Мировая торговля: сущность,
- •Тема 5 Внешнеторговая политика и практика
- •Тема 6. Международное движение капитала
- •Тема 7. Международная трудовая миграция
- •Тема 8 Валютные отношения и валютная
- •Тема10. Механизм регулирования
- •Форма и её описание
2. Решение типовых задач.
Пример №1.
По семи территориям района известны значения двух признаков (табл.2.1)
Таблица 2.1.
|
№ района |
Расходы на покупку продовольственных товаров в общих расходах, %, у |
Среднедневная заработная плата одного работающего, руб.,х |
|
1 |
68,8 |
45,1 |
|
2 |
61,2 |
59,0 |
|
3 |
59,9 |
57,2 |
|
4 |
56,7 |
61,8 |
|
5 |
55 |
58,8 |
|
6 |
54,3 |
47,2 |
|
7 |
49,3 |
55,2 |
Требуется:
Для характеристики зависимости у от х рассчитать параметры следующих функций:
линейной;
степенной;
показательной;
равносторонней гиперболы.
Оценить качество модели через среднюю ошибку аппроксимации Ā и F- критерий Фишера.
РЕШЕНИЕ.
Для расчета параметров а и b линейной регрессии у = а + bx решаем систему нормальных уравнений относительно а и b:
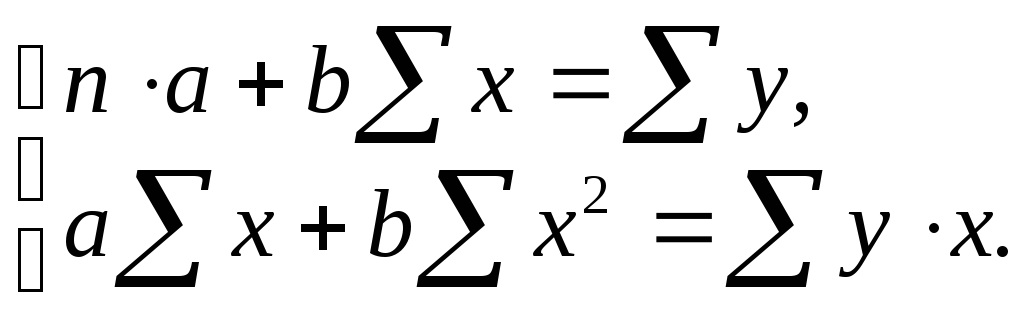
Составим расчетную таблицу:
|
|
у |
х |
ух |
х2 |
у2 |
ŷх |
у- ŷх |
Аi |
|
1 |
68,8 |
45,1 |
3102,88 |
2034,01 |
4733,44 |
61,3 |
7,5 |
10,9 |
|
2 |
61,2 |
59,0 |
3610,8 |
3481,00 |
3745,44 |
56,5 |
4,7 |
7,7 |
|
3 |
59,9 |
57,2 |
3426,28 |
3271,84 |
3588,01 |
57,1 |
2,8 |
4,7 |
|
4 |
56,7 |
61,8 |
3504,06 |
3819,24 |
3214,89 |
55,5 |
1,2 |
2,1 |
|
5 |
55 |
58,8 |
3234 |
3457,44 |
3025,00 |
56,5 |
-1,5 |
2,7 |
|
6 |
54,3 |
47,2 |
3562,36 |
2227,84 |
2948,49 |
60,5 |
-6,2 |
11,4 |
|
7 |
49,3 |
55,2 |
2721,36 |
3047,04 |
2430,49 |
57,8 |
-8,5 |
17,2 |
|
Итого |
405,2 |
384,3 |
22162,34 |
21338,41 |
23685,76 |
405,2 |
0,0 |
56,7 |
|
Среднее значение |
57,89 |
54,9 |
3166,05 |
3048,34 |
3383,68 |
|
|
8,1 |
|
σ |
5,74 |
5,86 |
|
|
|
|
|
|
|
σ 2 |
39,92 |
34,34 |
|
|
|
|
|
|

Уравнение регрессии
имеет вид: ![]()
С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35%-ных пункта. Найдем линейный коэффициент парной корреляции:
![]()
Связь умеренная, обратная. Найдем коэффициент детерминации:
![]()
Вариация результата на 12,7% объясняется вариацией фактора х.
Величина средней ошибки аппроксимации равна:
![]()
В среднем расчетные значения отклоняются от фактических на 8,1%.
Рассчитаем F
– критерий Фишера: ![]() Fтабл=6,6.
Fтабл=6,6.
Так как Fтабл.>Fфакт, α=0,05, то принимается гипотеза Ho о статистически незначимых параметрах данного уравнения. Этот результат можно объяснить невысокой теснотой выявленной зависимости и небольшим числом наблюдений.
Построение степенной модели
 можно провести методом линеаризации
переменных. Линеаризация производится
путем логарифмирования обеих частей
уравнения:
можно провести методом линеаризации
переменных. Линеаризация производится
путем логарифмирования обеих частей
уравнения:

Для расчетов параметров удобно данные представить в виде следующей таблицы:
|
|
У |
Х |
УХ |
У2 |
Х2 |
|
|
|
|
|
1 |
1,84 |
1,65 |
3,04 |
3,38 |
2,74 |
61 |
7,8 |
60,8 |
11,3 |
|
2 |
1,79 |
1,77 |
3,16 |
3,19 |
3,14 |
56,3 |
4,9 |
24 |
8,0 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
Итого |
12,32 |
12,16 |
21,4 |
21,71 |
21,16 |
403,5 |
1,7 |
197,9 |
56,3 |
|
Среднее значение |
1,76 |
1,74 |
3,06 |
3,101 |
3,019 |
|
|
28,27 |
8,0 |
|
σ |
0,0425 |
0,0484 |
|
|
|
|
|
|
|
|
σ2 |
0,0018 |
0,0023 |
|
|
|
|
|
|
|
Найдем С и b:

Линейное уравнение
имеет вид: ![]() .
.
Выполним потенцирование уравнения, получим:
![]()
Рассчитаем показатель тесноты связи – индекс корреляции ρху :

Построению уравнения
показательной кривой ![]() предшествует процедура линеаризации
переменных при логарифмировании обеих
частей уравнения:
предшествует процедура линеаризации
переменных при логарифмировании обеих
частей уравнения:
![]()
Уравнение равносторонней гиперболы
 линеаризуется при замене:
линеаризуется при замене:  Тогда
Тогда 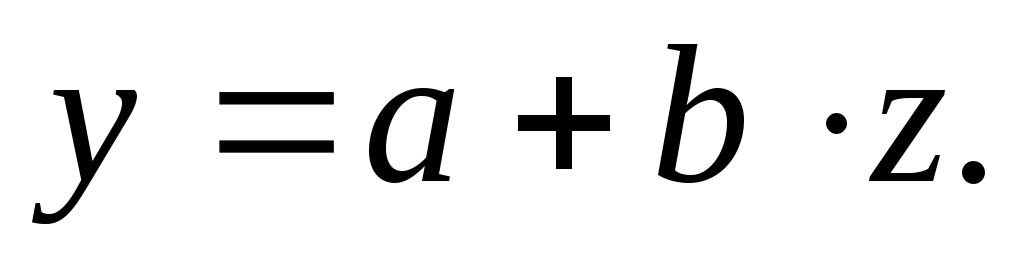
Пример № 2.
По территориям региона имеются данные (табл.2.2).
|
Номер региона |
Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х |
Среднедневная заработная плата, руб., у |
|
1 |
78 |
133 |
|
2 |
82 |
148 |
|
3 |
87 |
134 |
|
4 |
79 |
154 |
|
5 |
89 |
162 |
|
6 |
106 |
195 |
|
7 |
67 |
139 |
|
8 |
88 |
158 |
|
9 |
73 |
152 |
|
10 |
87 |
162 |
|
11 |
76 |
159 |
|
12 |
115 |
173 |
Требуется :
Оценить статистическую значимость параметров регрессии и корреляции.
Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х, 110% от среднего уровня.
Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
РЕШЕНИЕ.
1. Для расчета параметров уравнения линейной регрессии используем ППП Excel инструмент анализа данных Регрессия. Получены следующие данные: r = 0,7201; r2= 0,52; коэффициенты: a=76,9, b=0,92.
Уравнение регрессии
имеет вид: ![]()
Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента. Выдвинем гипотезу Но о статистически незначимом отличии показателей от нуля: a=b=rxy=0.
tтабл = 2,23 для числа степеней свободы df=n-2=12-2=10 и α=0,05.
Определим случайные ошибки та, тb, тr:

Тогда
![]()
Фактические значения t-статистики превосходят табличное значение tтабл=2,23; поэтому гипотеза Но отклоняется, т.е. а,b, r не случайно отличаются от нуля, а статистически значимы.
Для расчета доверительного интервала определим предельную ошибку ∆ для каждого показателя:
![]()
Доверительные интервалы имеют следующий вид:
![]()
Вывод: с вероятностью р=1-α=1-0,05=0,95 параметры а и b, находясь в указанных границах, не принимают нулевых значений, т.е. являются статистически значимыми.
2. Используем полученные оценки уравнения регрессии для его прогноза. Прогнозное значение прожиточного минимума составит:
![]() тыс. руб.,
тыс. руб.,
тогда ![]() тыс. руб.
тыс. руб.
3. Вычислим среднюю стандартную ошибку прогноза:
 где
где ![]()
Предельная ошибка
прогноза, которая в 95% случаев не будет
превышена, составит: ![]()
Доверительный интервал прогноза:
![]() ,
,
![]()
