5.1.1. Визначення значущості коефіцієнтів рівняння

Рівень значущості – це величина α =1–Р, де Р – заданий рівень надійності (довірча ймовірність).

Режим роботи інструменту Регресія використовує за умовчанням рівень надійності Р=0,95. Для цього рівня надійності рівень значущості рівний α = 1 – 0,95 = 0,05. Цей рівень значущості вважається за заданий.

У інструменті Регресія надбудови Пакет аналізу для кожного з коефіцієнтів а₀ і а₁ обчислюється рівень його значущості α_р, який вказаний у результативній таблиці (табл. 2.7 термін "Р-значення"). Якщо розрахований для коефіцієнтів а₀, а₁ рівень значущості α_р, менше заданого рівня значущості α= 0,05, то цей коефіцієнт визнається невипадковим (тобто типовим для генеральної сукупності), інакше – випадковим.

Примітка. У випадку, якщо визнається випадковим вільний член а₀, то рівняння регресії доцільно побудувати наново без вільного члена а₀. У цьому випадку в діалоговому вікні Регресія необхідно задати ті ж самі параметри лише того, що слід активізувати прапорець Константа-нуль (це означає, що модель будуватиметься за умови а₀=0). У лабораторній роботі такий крок не передбачений.

Якщо незначущим (випадковим) є коефіцієнт регресії а₁, то взаємозв'язок між ознаками X і Y в принципі не може апроксимуватися лінійною моделлю.

Висновок:

Для вільного члена а₀ рівняння регресії розрахований рівень значущості становить α_р = 0,7993. Оскільки він більше заданого рівня значущості α=0,05, то коефіцієнт а₀ визнається випадковим.

Для коефіцієнта регресії а₁ розрахований рівень значущості становить α_р =0,1984. Оскільки він більше заданого рівня значущості α=0,05, то коефіцієнт а₁ визнається випадковим.

5.1.2. Залежність довірчих інтервалів коефіцієнтів рівняння від заданого рівня надійності

Довірчі інтервали коефіцієнтів а₀, а₁ побудованого рівняння регресії при рівнях надійності Р=0,95 і Р=0,683 представлені в табл. 2.7, на основі якої формується табл. 2.9.

Таблиця 2.9

Межі довірчих інтервалів коефіцієнтів рівняння

Коефіцієнти	Межі довірчих інтервалів
	Для рівня надійності Р=0,95		Для рівня надійності Р=0,683
	нижня	Верхня	нижня	верхня
а0	-2,2591	1,6289	-1,2733	0,64315
а1	-0,0016	0,0073	0,00065	0,00506

Висновок:

У генеральній сукупності банків значення коефіцієнта а₀ слід чекати з ймовірністю Р=0,95 у межах -2,2591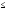а₀ 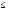1,6289, значення коефіцієнта а₁ у межах -0,0016а₁ 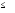0,0073 Зменшення рівня ймовірності веде до звуження довірчих інтервалів коефіцієнтів рівняння.

Визначення практичної придатності побудованої ої регресійної моделі.

Практичну придатність побудованої моделі 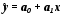можнаохарактеризувати за величиною лінійного коефіцієнта кореляції r:

• близькість 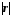до одиниці свідчить про хорошу апроксимацію фактичних даних за допомогою побудованої лінійної функції зв'язку;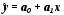

• близькість 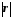до нуля означає, що зв'язок між фактичними данимиХ і Y не можна апроксимувати як за побудованою, так і будь-якою іншою лінійною моделлю, і, отже, для моделювання зв'язку слід використовувати яку-небудь відповідну нелінійну модель.

Придатність побудованої регресійної моделі для практичного використання можна оцінити і за величиною індексу детермінації R², який показує, яка частина загальної варіації ознаки Y пояснюється в побудованій моделі варіацією чинника X.

У основі такої оцінки лежить рівність R = 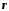, а також шкала Чеддока, що встановлює якісну характеристику щільності зв'язку залежно від величини .

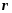Згідно шкали Чеддока високий ступінь щільності зв'язку ознак досягається лише при 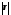>0,7, тобто при 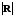>0,7. Для індексу детермінації R² це означає виконання нерівності R² >0,5.

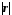
При недостатньо щільному зв'язку ознак X, Y (слабка, помірна, помітна) має місце нерівні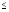сть 0,7, а отже, і нерівність .

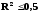З урахуванням вищесказаного, практична придатність побудованої моделі зв'язку 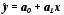оцінюється за величиною R² таким чином:

• нерівність R² >0,5 дозволяє вважати, що побудована модель придатна для практичного застосування, оскільки в ній досягається високий ступінь щільності зв'язку ознак X і Y, при якій більше 50% варіації ознаки Y пояснюється впливом чинника Х;

• нерівність 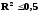означає, що побудована модель зв'язку практичного значення не має, зважаючи на недостатню щільність зв'язку між ознаками X і Y, при якій менше 50% варіації ознаки Y пояснюється впливом чинника Х, і, отже, чинник Х впливає на варіацію Y в значно меншій мірі, ніж інші (невраховані в моделі) чинники.

Значення індексу детермінації R² наводиться в табл. 2.5 в комірці В79 (термін "R - квадрат").

Висновок:

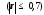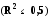Значення лінійного коефіцієнта кореляції r і значення індексу детермінації R² згідно таблиці. 2.5 рівні: r = 0,27836, R² =0,07749. Оскільки і _, то побудована лінійна регресійна модель зв'язку не придатна для практичного використання.