2. Растяжение – сжатие статически определимых ступенчатых стержней

Д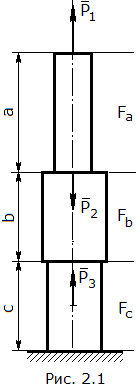ано: стержень нагружен системой сил (рис. 2.1).

материал – сталь, [σ] = 160 МПа, E = 2∙10⁵ МПа.

a = 80 см, F_a = 4 см², P₁ = 180 кН;

b = 30 см, F_b = 12 см², P₂ = 140 кН;

c = 60 см, F_c = 10 см², P₃ = 110 кН;

Вычислить:

1. построить эпюры продольных сил, напряжений и перемещений;

2. оценить прочность стержня;

Решение:

1. Построение эпюр, продольных сил, напряжений и перемещений

Заданный стержень имеет 4 участка, границами участков являются сечения приложенения внешних сил и места изменения размеров поперечного сечения (рис. 2.2, а).

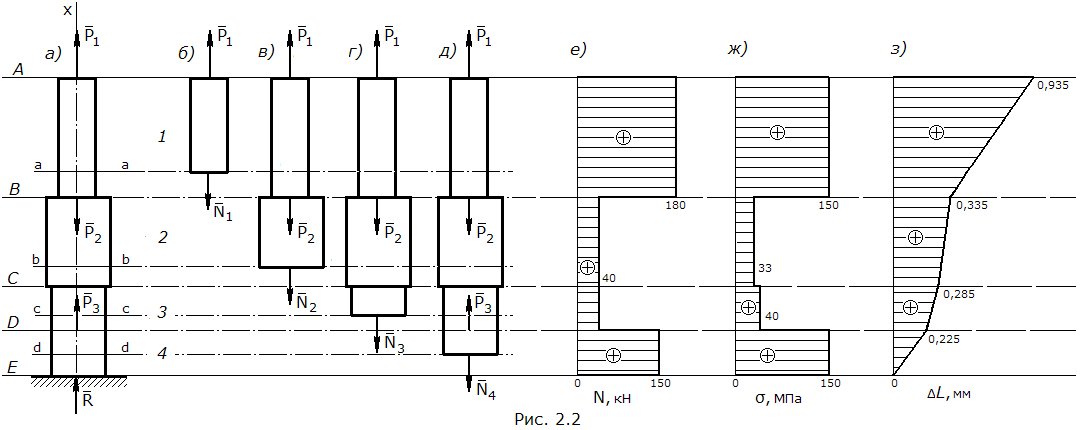
Для определения продольных сил проводим произвольные сечения на каждом из участков (се-чение a–a на участке 1, b–b на участке 2, c–c на участке 3, d–d на участке 4) и рассматриваем рав-новесие верхней отсеченной части стержня (рис. 2.2, б, в, г, д):

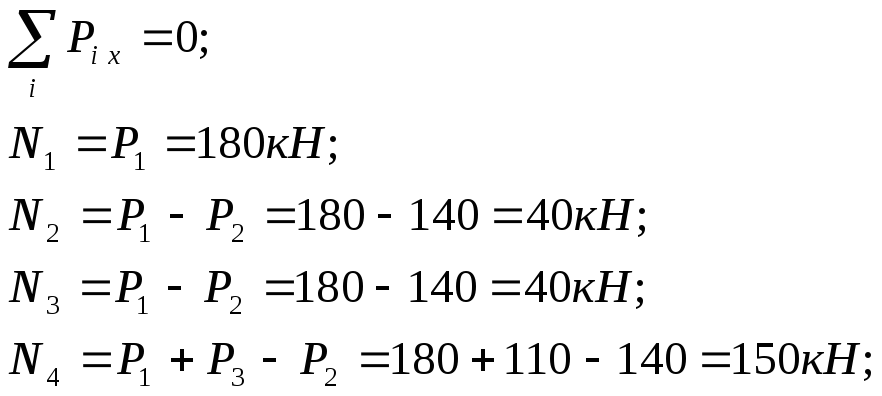
Определяем нормальные напряжения в сечениях каждого участка:

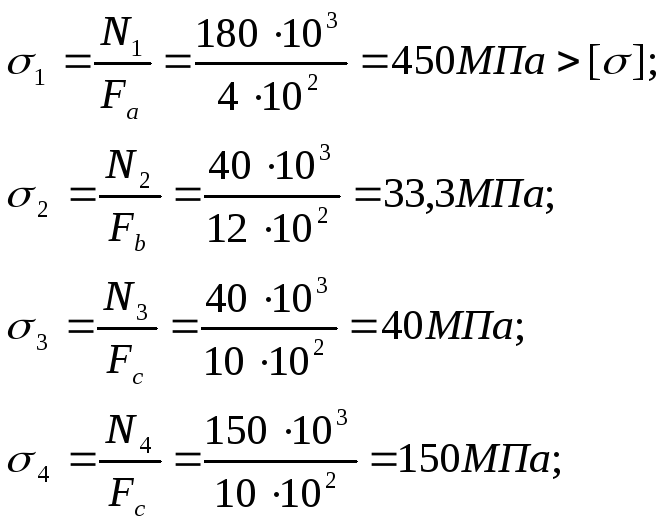
Таким образом, 1^ый участок стержня испытывает напряжения превышающие допустимые поэтому подбираем исходя из условия прочности новое сечения:

Берем новое сечение участка стержня равное , тогда нормальное напряжение, воз-никающее в сечении участка будет:

Строим эпюры для продольных сил и нормальных напряжений (рис. 2.2, е, ж).

Определяем удлинения участков стержня, считая длины участков стержня следующими:

Удлинения участков стержня – есть перемещение сечений границ участка относительно друг друга, абсолютное перемещение сечения – есть перемещение сечения относительно заделки. Для нахождения абсолютного перемещения сечения, необходимо просуммировать относительные перемещения сечений до данного, начиная от заделки, т.е.:

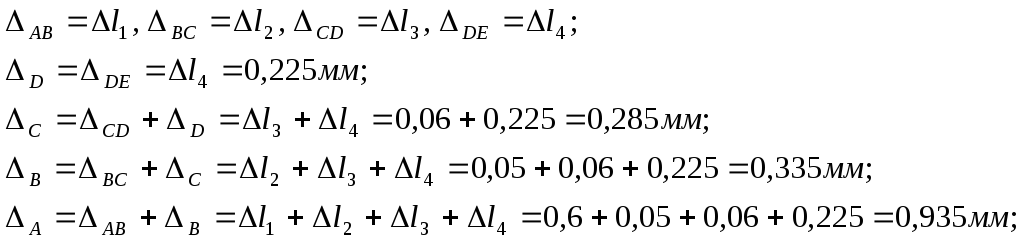
Строим эпюру абсолютных перемещений, начиная с закрепленного конца (рис. 2.2, з).

2. Оценка прочности стержня

При начальных данных прочность стержня не была достаточна, чтобы выдержать приложен-ные нагрузки: в сечении участка 1 возникали напряжения, превышающие допустимые, поэтому было необходимо пересчитать площадь поперечного сечения 1^ого участка для выполнения условия прочности, что и было сделано в п. 1.

3. Проверка прочности балки и исследование деформаций при изгибе

Д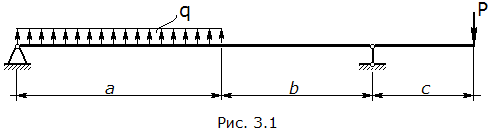ано: балка нагружена системой сил (рис. 3.1).

материал – сталь Ст 3, [σ] = 160 МПа, [τ] = 100 МПа, Е = 2·10⁵ МПа.

q = 20 кН/м, P = 20 кН;

a = 4 м, b = 3 м, c = 2 м;

Требуется:

1. составить уравнение поперечных сил и изгибающих моментов по участкам, построить эпюры (Q и M_и);

2. подобрать сечение балки-двутавра из условия прочности по нормальным напряжениям;

3. вычислить максимальное касательное напряжение;

4. определить главное напряжение в сечении, имеющем одновременно большие значения Q и М_и для точки сечения на уровне примыкания полки к стенке; проверить прочность по энергетиче-ской теории.

5. определить прогибы и углы поворота в характерных сечениях балки;

6. по вычисленным значениям прогибов показать на схеме балки её изогнутую ось;

7. проверить жесткость балки по допускаемому значению прогиба ;

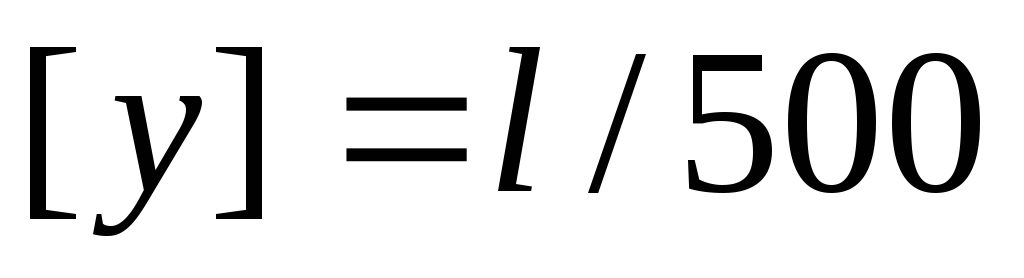Решение:

1. Составление уравнений поперечных сил и изгибающих моментов по участкам, построение эпюр

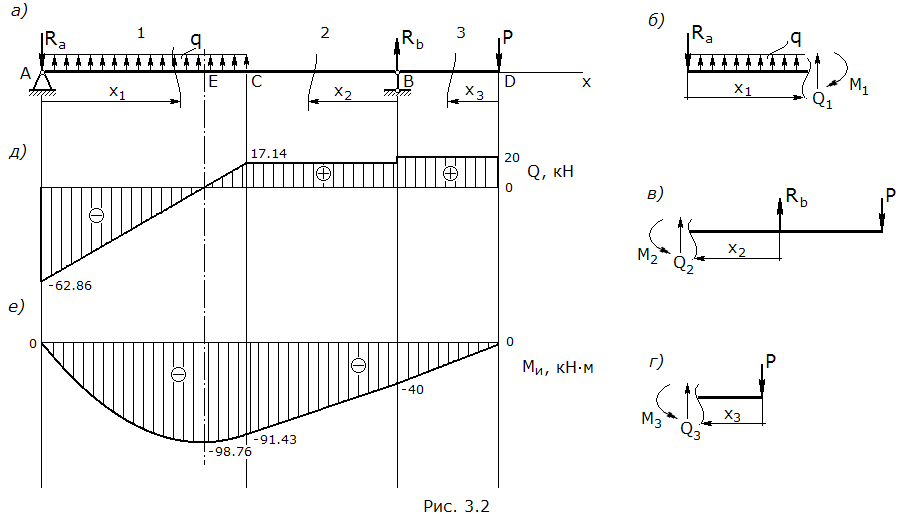
Определяем реакции опор, исходя из того, что суммы моментов внешних сил относительно опор равны нулю (рис. 3.2, а):

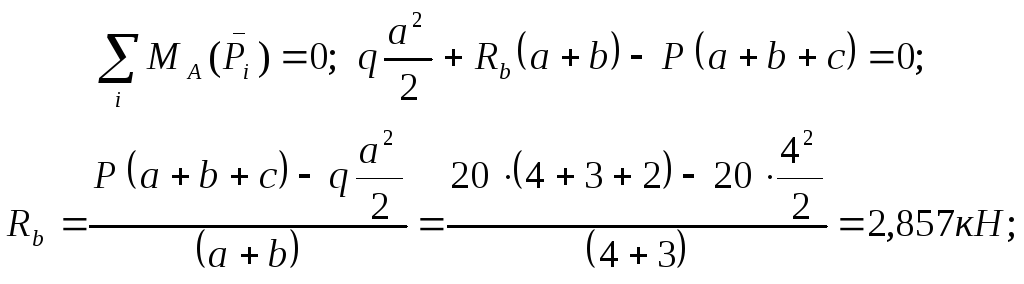
Равномерно распределенную нагрузку заменяем равнодействующей, приложенной в центре участка действия нагрузки и равной по величине .

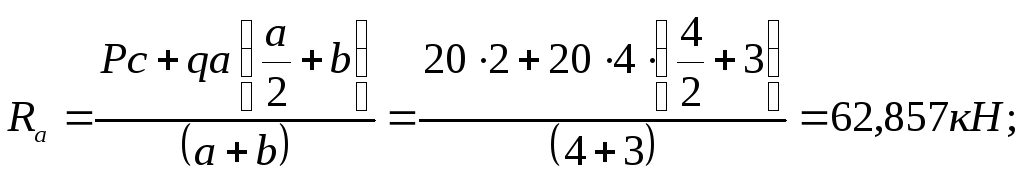
Заданная балка имеет 3 участка нагружения, границами участков являются сечения приложе-ния внешних сил. Определяем поперечные силы и изгибающие моменты по участкам.

На 1^ом участке проводим произвольное сечение и рассматриваем отсеченную часть (рис. 3.2, б). На участке действуют две внешние силы: реакция опоры R_a и распределенная на-грузка (следовательно, поперечная сила будет меняться по линейному закону), при этом реакция R_a стремится повернуть отсеч. часть против часовой стрелки и определяемая ей составляющая поперечной силы имеет отрицательный знак, распределенная нагрузка стремится повернуть отсеч. часть по часовой стрелке и определяемая ей составляющая поперечной силы имеет поло-жительный знак; поперечная сила есть сумма этих составляющих:

в сечении A поперечная сила равна:

в сечении C:

Поскольку на участке присутствует распределенная нагрузка, то изгибающий момент будет меняться по квадратичному закону; реакция R_a загибает отсеч. часть выпуклостью вверх и момент, создаваемый ей отрицательный, распределенная нагрузка загибает отсеч. часть выпуклостью вниз и момент, создаваемый ей положителен; тогда изгибающий момент будет:

в сечении A изгибающий момент равен 0 (нет внешнего момента), в сечении C:

В сечении балки, где поперечная сила равна 0, изгибающий момент принимает максимальное значение (сечение E):

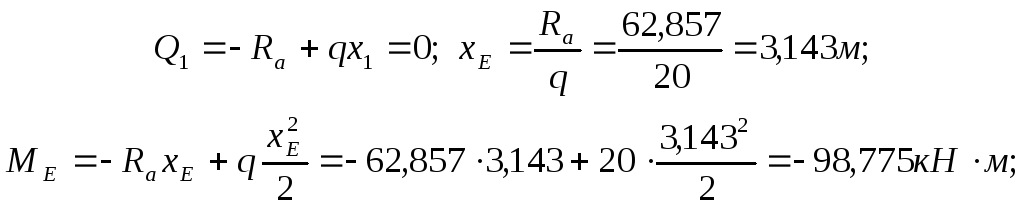
На 2^ом участке проводим сечение и рассматриваем отсеч. часть (рис. 3.2, в). На участке дей-ствуют две внешние силы: реакция опоры R_b и сила P (следовательно, поперечная сила на участке постоянна), при этом реакция опоры стремится повернуть отсеч. часть против часовой стрелки, а сила P по часовой стрелке, поэтому:

Изгибающий момент меняется линейно (т.к. поперечная сила постоянна), при этом реакция опоры загибает отсеч. часть выпуклостью вниз, сила P выпуклостью вверх, поэтому:

в сечении C изгибающий момент равен:

в сечении B:

На 3^ем участке проводим сечение и рассматриваем отсеч. часть (рис. 3.2, г). На участке дей-ствует одна внешняя сила: сила P (следовательно, поперечная сила на участке постоянна):

Изгибающий момент меняется линейно (т.к. поперечная сила постоянна), при этом сила P за-гибает отсеч. часть выпуклостью вверх, поэтому:

в сечении B изгибающий момент равен:

в сечении D изгибающий момент равен 0 (нет внешнего момента).

По приведенным данным строим эпюру поперечных сил (рис. 3.2, д) и изгибающих моментов (рис. 3.2, е).

2. Подбор сечения балки-двутавра из условия прочности по нормальным напряжениям

Максимальное нормальное напряжение, возникающее в сечении балки при изгибе, равно:

по условию прочности максимальное нормальное напряжение не должно превышать допустимого, поэтому:

подставляя в выражение максимальный изгибающий момент, возникающий в сечениях балки (в данном случае в сечение E), получаем:

Для обеспечения требуемой прочности можно:

– по сортаменту двутавровых балок (ГОСТ 8239–72) выбрать двутавр №36, для кото-рого W_z=743 см³ и масса 1^ого метра балки 48,6 кг;

– по сортаменту швеллеров (ГОСТ 8240–72) выбрать швеллер №27, для которого W_z=310 см³ и масса 1^ого метра балки 27,7 кг, и соединив два швеллера, получить необходимое се-чение;

Поскольку масса 1^ого метра двутавра меньше массы 1^ого метра двух скрепленных швеллеров на 14%, при этом момент сопротивления двутавра больше суммы моментов сопротивления двух швеллеров на 20%, то рационально будет использовать двутавровую балку для обеспечения проч-ности конструкции.

Выбираем двутавровую балку №36, для которого момент сопротивления W_z = 743 см³, мо-мент инерции J_z = 13380 см⁴, площадь сечения двутавра F = 61,9 см², статический момент полусечения S_max = 423 см³;

Тогда максимальное нормальное напряжение, возникающее в сечении балки, будет:

Нормальные напряжения в сечении изменяются линейно: максимальны по краям и равны 0 на нейтральной линии; т.к. изгибающий момент в сечении отрицателен, то верхние слои материала растягиваются и нормальные напряжения положительны, нижние слои сжимаются и нормальные напряжения отрицательны. Строим эпюру нормальных напряжений в сечении E (рис. 3.3, б).

3. Вычисление максимального касательного напряжения

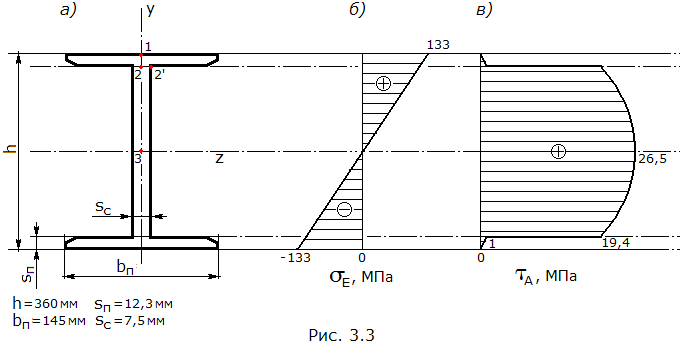
Касательные напряжения, возникающие в сечениях балки при изгибе, определяются по фор-муле Журавского:

где Q – поперечная сила, действующая в сечении, S_z^отс – статический момент отсеч. части сечения относительно оси z, b – ширина сечения в рассматриваемом слое материала.

Максимальные касательные напряжения возникают в сечении, где поперечная сила макси-мальна (сечение A), поэтому:

Определяем касательные напряжения в характерных точках сечения двутавровой балки (рис. 3.3, а):

– т. 1:

Статический момент отсеч. части S_z^отс = 0 (точка находится на краю сечения), поэтому по формуле Журавского касательные напряжения

– т. 2:

Статический момент отсеч. части равен:

где F_отс – площадь осеч. части сечения, y_{C отс} – расстояние от оси z до центра тяжести отсеч. части.

В данном случае отсеч. частью является часть сечения двутавра выше т. 2, т.е. полка; тогда площадь сечения полки примерно будет:

где b_п – ширина полки, s_п – средняя толщина полки (рис. 3.3, а).

Центр тяжести сечения полки находится приблизительно на половине толщины полки от края полки, расстояние от оси z до центра тяжести:

где h – высота сечения двутавра, s_п – средняя толщина полки (рис. 3.3, а).

Статический момент полки относительно оси z:

Ширина сечения на уровне т. 2 равна толщине стенки s_с; тогда касательные напряжения в т. 2 сечения равны:

– т. 2’:

Статический момент отсеч. части равен статическому моменту полки (т. 2 и т. 2’ находятся на одном уровне относительно оси z). Отличие между т. 2 и т. 2’ состоит в том, что ширина сечения на уровне т. 2 равна толщине стенки, на уровне т. 2’ – ширине полки, поэтому касательные напря-жения в т. 2’ сечения равны:

– т. 3:

Статический момент отсеч. части равен статическому моменту полусечения S_max; ширина се-чения на уровне т. 3 равна толщине стенки s_с, тогда касательные напряжения в т. 3 сечения равны:

Касательное напряжение, возникающее в т. 3 сечения A, является максимальным для данного сечения, но т.к. в рассмотренном сечении A возникают максимальные касательные напряжения во всей балке, то касательное напряжение в т. 3 является максимальным для всей балки:

Максимальное касательное напряжение не превышает допустимого.

По приведенным вычислениям строим эпюру касательных напряжений для сечения A (рис. 3.3, в).

4. Определение главного напряжения в сечении, имеющем одновременно большие значения Q и М_и для точки сечения на уровне примыкания полки к стенке; проверка прочности по энергетиче-ской теории

В качестве сечения, имеющего одновременно большие значения Q и M_и, берем сечение C, для которого поперечная сила Q_C =  17,143 кН, и изгибающий момент M_C = -91,428 кН∙м.

Так как нормальные напряжения линейно изменяются по высоте сечения, то наибольшее действующее в сечение C равно:

Нормальное напряжение, действующее на расстоянии y от нейтральной линии, будет:

где h – высота сечения двутавра, y_max – наибольшее расстояние от нейтральной линии до края сече-ния; нормальное напряжение на уровне примыкания полки к стенке (т. 2’ на рис. 3.3, а):

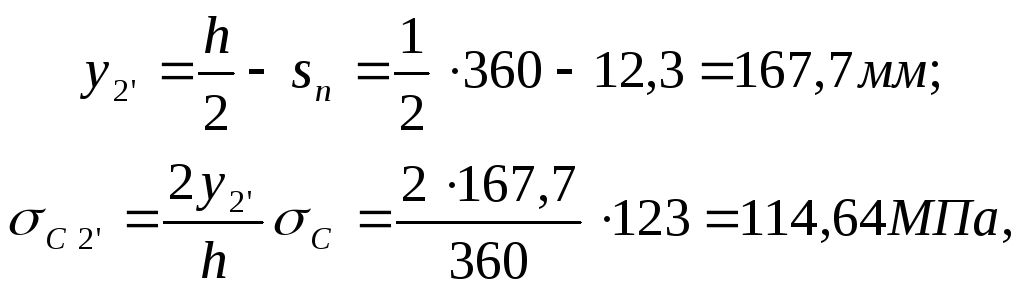
где y_2’ – расстояние от нейтральной линии до полки.

Касательное напряжение в точке примыкания полки к стенке (т. 2’ на рис. 3.3, а), по формуле Журавского (с учетом ранее вычисленного статического момента полки):

где S_z^отс – статический момент полки относительно оси z, b_п – ширина полки

Главные напряжения для выделенного элемента в точке примыкания полки к стенке опреде-ляются по формулам для плоского напряженного состояния:

в данном случае и тогда:

IV теория прочности (для пластичных материалов) – энергетическая теория, предполагается, что опасное состояние нагруженного элемента определяется предельной величиной накопленной удельной энергии формоизменения. Эквивалентное напряжение и условие прочности определя-ется как:

Подставляя в это выражение выражения для главных напряжений, вычисленные выше, и при-водя подобные, получаем условие прочности:

в данном случае, подставляя нормальные и касательные напряжения для точки примыкания полки к стенке сечения, получаем:

т.е. условие прочности выполняется.

5. Определение прогибов и углов поворота в характерных сечениях балки

Методом начальных параметров составляем уравнения для прогибов: ось x направляем вправо, y – вверх; начало отсчета берем в сечении A, составляем уравнение моментов относи-тельно сечения D. Все силовые факторы имеют знаки моментов: реакция R_a загибает балку относительно сечения D выпуклостью вверх и создаваемый ей момент отрицателен, реакция R_b – выпуклостью вниз и создаваемый ей момент положителен, распределенная нагрузка – выпук-лостью вниз и создаваемый ей момент положителен, но т.к. распределенная нагрузка не доходит до конца балки, то продолжаем ее до конца и прикладываем компенсирующую, момент создава-емый компенсирующей нагрузкой отрицателен. Составляем уравнение прогибов:

уравнение углов поворота получается дифференцированием уравнения прогибов:

Г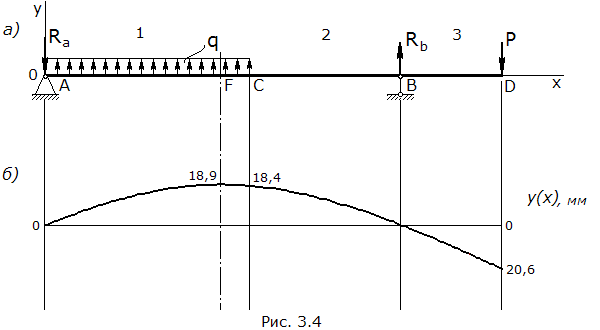раничными условиями является то, что прогиб в сеченияхA и B (т.е. под опо-рами) равен 0:

из 1^ого граничного условия получаем:

из 2^ого граничного условия:

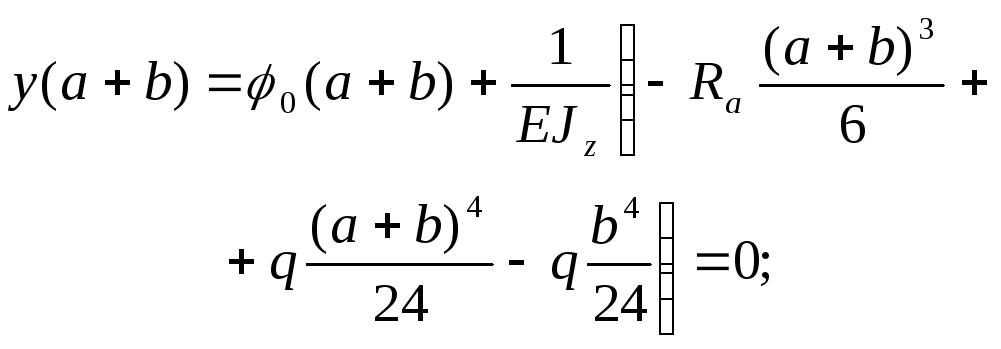откуда получаем:

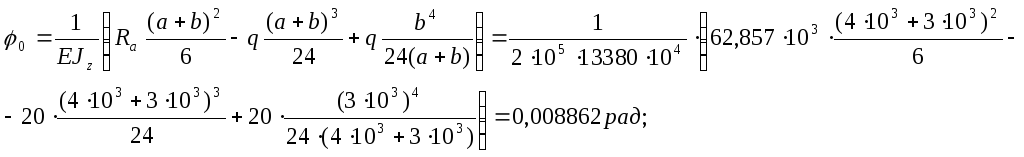
Углы поворота в сечениях A и B:

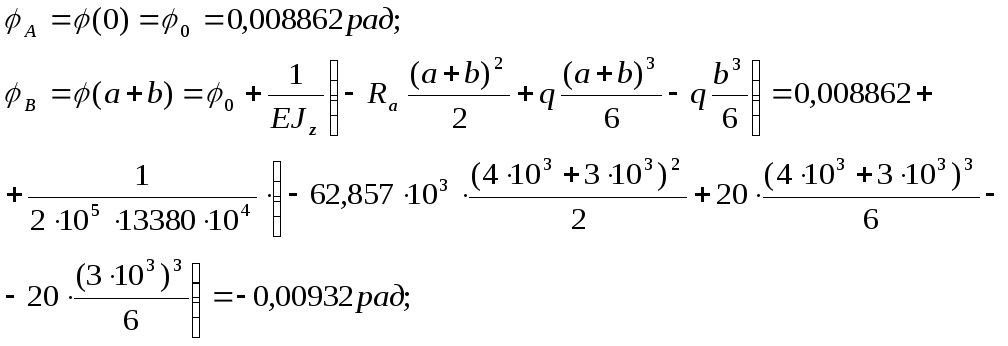
Определяем значения прогибов и углов поворота в сечениях балки:

прогиб в сечении C:

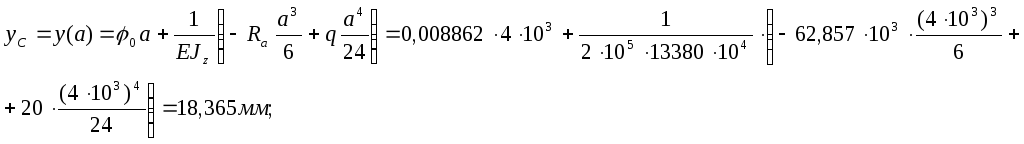
угол поворота в сечении C:

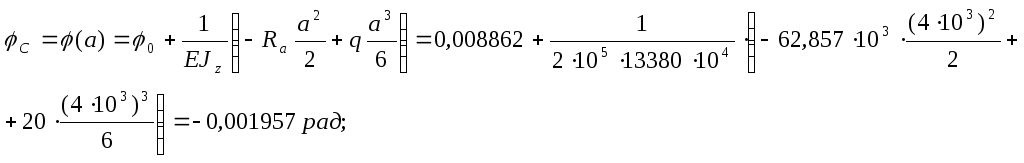
прогиб в сечении D:

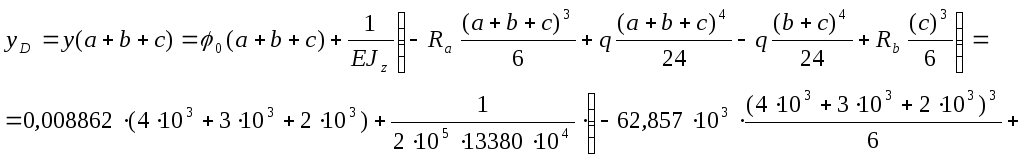
угол поворота в сечении D:

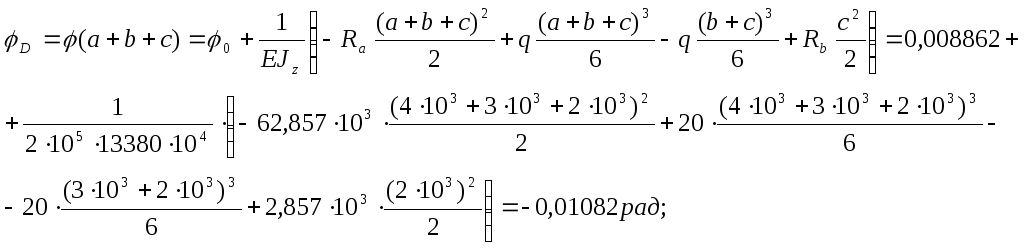
Из расчетов видно, что на 1^ом участке угол поворота меняется с положителного на отрица-тельный, в отличие от других участков, где угол поворота монотонно убывает; значит на 1^ом участ-ке есть такое сечение, где угол поворота равен 0, – это сечение соответствует перегибу балки и ее максимальному на этом участке прогибу, т.е.

где x_F – расстояние от края балки до сечения F перегиба балки.

Решая это кубическое уравнение методом Кардано, получаем 3 действительных корня (описа-ние метода и решение уравнения опущено вследствие его громоздкости), при этом в диапазоне [0;4] лежит только один корень

Прогиб в сечении F равен:

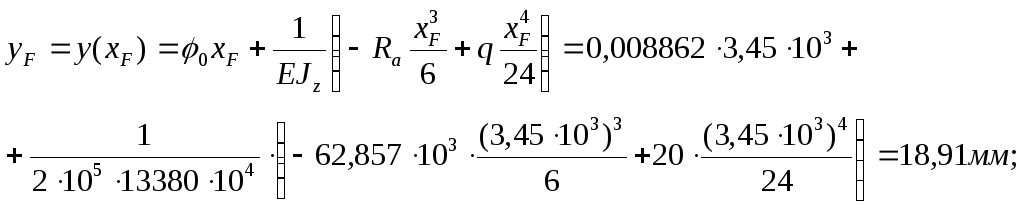
6. Показ изогнутой оси балки

По вычисленным в п. 5 значениям прогибов показываем изогнутую ось балки (рис. 3.4, б).

7. Проверка жесткости балки по допускаемому значению прогиба

Проверяем жесткость балки по допускаемому прогибу на каждом из участков балки.

– 1^ый участок:

Допускаемый прогиб для 1^ого участка равен:

где l₁ – длина 1^ого участка.

Наибольший прогиб на участке 1 равен прогибу в сечении F, поэтому условие жесткости по допускаемому прогибу будет:

таким образом, условие жесткости по допускаемому прогибу не выполняется.

– 2^ой участок:

Допускаемый прогиб для 2^ого участка равен:

где l₂ – длина 2^ого участка.

Наибольший прогиб на участке 2 равен прогибу в сечении C, поэтому:

условие жесткости по допускаемому прогибу также не выполняется.

– 3^ий участок:

Допускаемый прогиб для 3^его участка равен:

где l₃ – длина 3^его участка.

Наибольший прогиб на участке 3 равен прогибу на краю участка – в сечении D, поэтому:

таким образом, и на этом участке условие жесткости по допускаемому прогибу не выполняется.