Лекция 7

Работа затрачиваемая на перемещение откатных частей.

Если обозначить вес Q₀, массу M и скорость V, то L₅=(MV²)/2=Q₀V²/2g.

Скорость отката можно найти на основании закона сохранения количества движения системы ствол – заряд – снаряд.

О



пределим скорости снаряда _a и заряда U (U*_ср). Для определения U*_ср допускаем, что масса заряда в каждый момент распределена в заснарядном пространстве равномерно и скорость U меняется по линейному закону от V у дна каморы до _a у дна снаряда. Причем _a= - V.

П ри линейном законе:

С оставим уравнение количества движения:

П одставляя в L₅ значение V, имеем:

Суммарный учет второстепенных работ.

П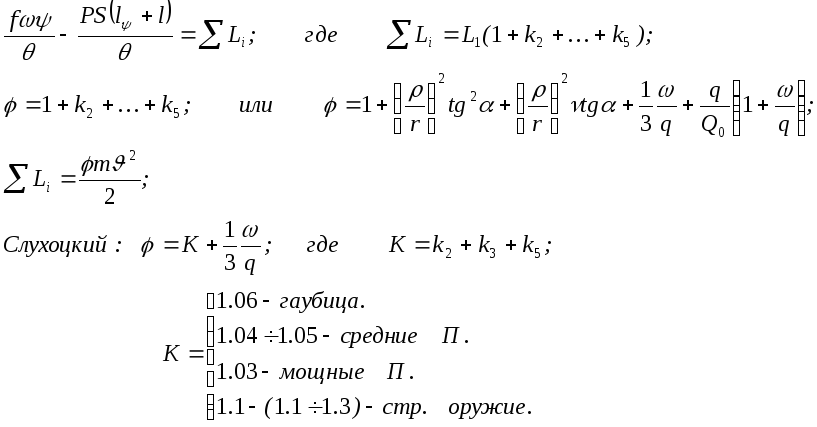 роведя исследование каждого вида работ и определив для них общее выражение в виде: L_i=k_i(m²/2)=k_iL₁ – можно составить аналитическое выражение для  всех работ в уравнении баланса энергии:

З ависимость между давлением на дно канала и дно снаряда.

Из закона сохранения количества движения:

У читывая, что M(dV/dt)= SP_дн и ₁m(d /dt)=SP_сн продифференцируем это уравнение:

Пологая, что 1+(1/2)(/M)1 получим:

П ри выводе основного уравнения ВБ принимают p=RT. Здесь PP_ср  среднебаллистическое давление. Принимается, что порох горит под этим давлением:

Умножим обе части преведущего равенства на ₁:

₁P=P_сн(₁+(1/3)(/q))=P_сн (-k₅)P_сн,

откуда P/=P_cн₁ или P_сн/P=₁/.

Тогда уравнение движения:

₁m(d/dt)=SP_сн эквивалентно m(d/dt)=SP,

где =1+k₂+...+k₅; ₁=1+k₂+k₃.

И основное уравнение ВБ может быть представлено в виде:

Т .е. в уравнение энергии и движения входят одни и те же величины P и .

Решение ОЗВБ.

ОЗВБ состоит в решении системы уравнений, выражающих закономерности процессов, протекающих при выстреле. Устанавливают связь между конструктивными данными канала ствола, и условиями заряжания P, , l, T, t, . Результат P(l), (l), P(t), (t), (l), T(l) и значения P_m и _g.

Исходные данные для решения ОЗВБ:

1. Конструкционные данные канала ствола:

d; S=n_sd²; W₀; l₀=W₀/S; l_кам=l₀/; l_g; _g=W_g/W₀=l_g/l₀; J_кан=l_кам+l_g; J_ств=J_кан+l_затв.

2. Условия заряжания.

Снаряд: q, (/r)²,  ₀.

Природа пороха: , , , u₁, .

Форма и размеры пороха: 2e₁, 2b, 2с, , , Y_k=e₁/u₁.

Заряд: , =/W₀, /q.

Воспламен.: _b, _b, _b.

Методы решения: эмпирический, численный, аналитический, табличный.

Решение ОЗВБ аналитическим методом.

С истема уравнений:

Основные допущения:

1. Закон горения геометрический.

2. Порох горит при среднем давлении P (P_дн>P>P_сн).

3. Закон скорости горения u=u₁p.

4. Второстепенные работы  основным и учит.  .

5. Теплоотдача не учитывается ( или  -учит.)

6. Состав продуктов горения не меняется (f и  =const).

7. Показатель =k-1 – const средний по вел.

8. Работа врезания не учитывается, врезание принимается мгновенным, при P=P₀ начинается движение.

9. Движение снаряда рассматривается с момента t_g.

10. Растяжение стенок ствола и прорыв ПГ через зазор между стволом иснарядом не учитывается.

Аналитический метод решения ОЗВБ В. Е. Слухоцкого (метод l_ср).

Аргумент z=e/e₁.; P_b P  P₀; W_кн=const; P₀ – задано.

З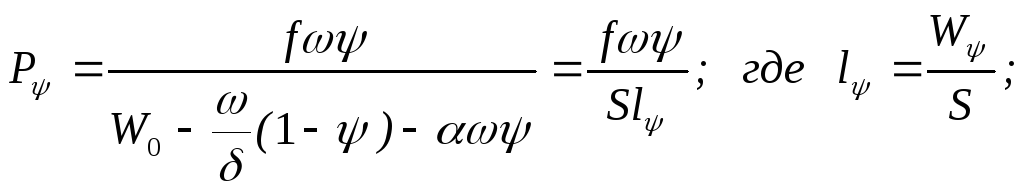 апишем уравнение пиростатики:

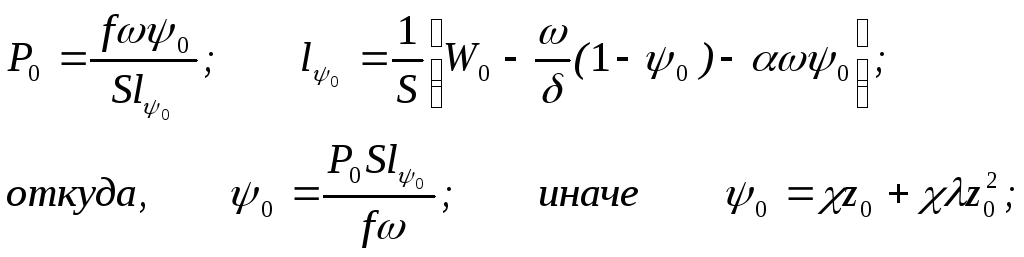В конце периода:

Т.к. z₀0.03 и 0.05 0.06 то можно принять ₀ z₀ или z₀=₀/=(P₀Sl_0)/().

В виду малости величины ­₀<0.1 можно принять l_0=l_=(W₀-/)/S. Определим ₀=1+2z₀ (₀0.987).

Результаты сводят в таблицу:

		z	l	P		t	
Начало горения	0	0	0	0 (Pb)	0	0	1
Конец периода	0	z0	0	P0	0	t0	0

Решение ОЗВБ I периода (дегрессивный П).

Должны получить таблицу:

		z	l	P		t	
Начало движения снаряда	0	z0	0	P0	0	t0	0
Конец горения пороха	1	1	lk	Pk	k	tk	k

Аргумент z; l(z); (z); P(z); (z).

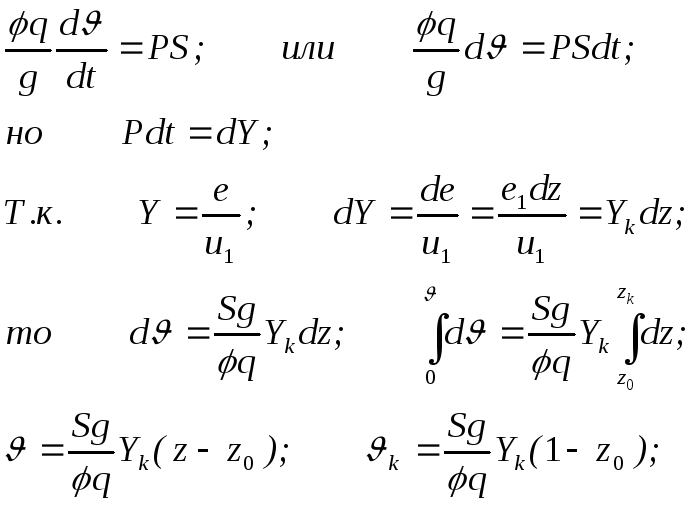1. З ав-ть (z):

З ависимость P(z) из основного уравнения ВБ:

П одставим в выражение =z(1+z):

В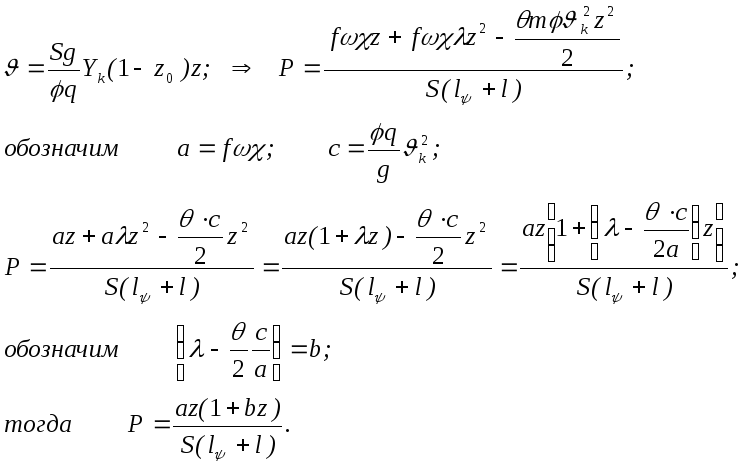 ернемся к выражению для скорости. С небольшой погрешностью можно принять =_kz (т.к. z₀0) т.е. можно записать:

Теперь необходимо определить l(z).

36