Лекция 6

Сопротивление при врезании пояска в нарезы. Давление форсирования.

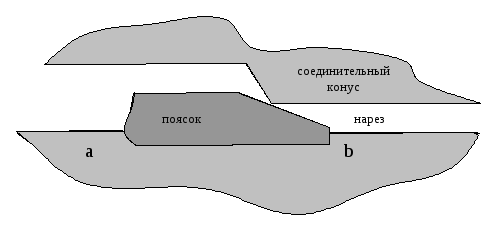
P

– общие орудия.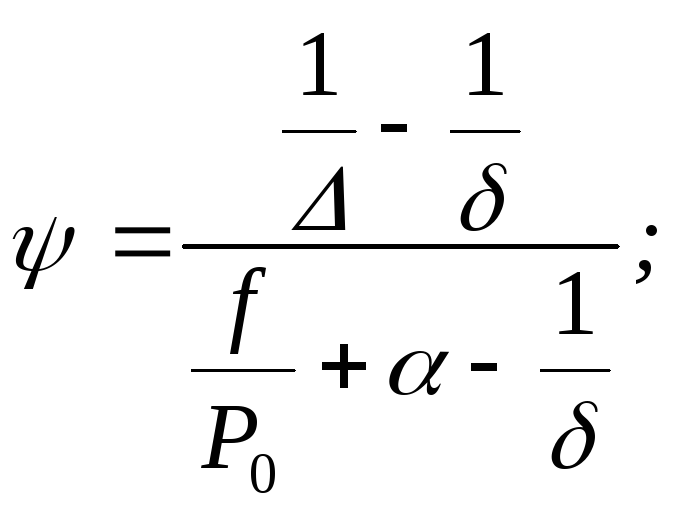

₀=П₀/S; P₀=1000-1500 кг/см² – стрелковые орудия; P₀=100 кг/см² – гладкоствольные орудия; P₀=const=300 кг/см².

Силы, возникающие на боевых гранях нарезов при движении снаряда.

Угол между ОКС и направлением нарезов вызывает силы реакции при движении снаряда по каналу ствола. Эти силы N направлены перпендикулярно поверхности соприкосновения и создают трение N вдоль боевой грани.

Под действием этих сил снаряду придается вращающее и поступательное движение. Определим силы N – реакции нареза и R – тормозящей силы. Изобразим развертку нареза т. А – центр боевой грани (силой Ф и Ф пренебрегаем.).

Разложим силы N и N по x и y.

N’=Ncos; N’’=N sin ;

N’=Ncos ; N’’=Nsin ;

На основе законов механики составим уравнения вращательного и поступательного движения:

1. д 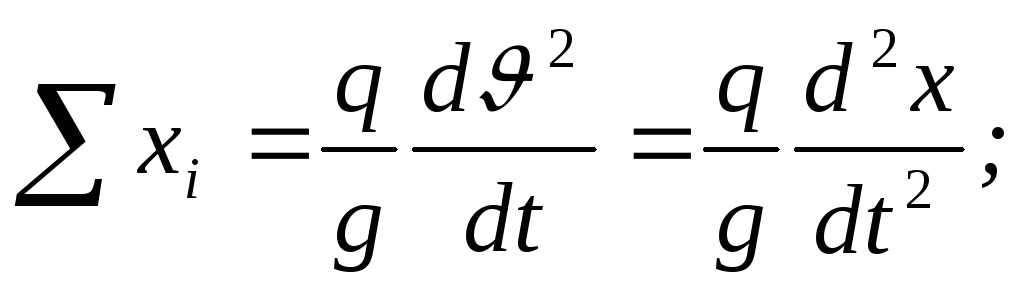ля поступательного:

2. д 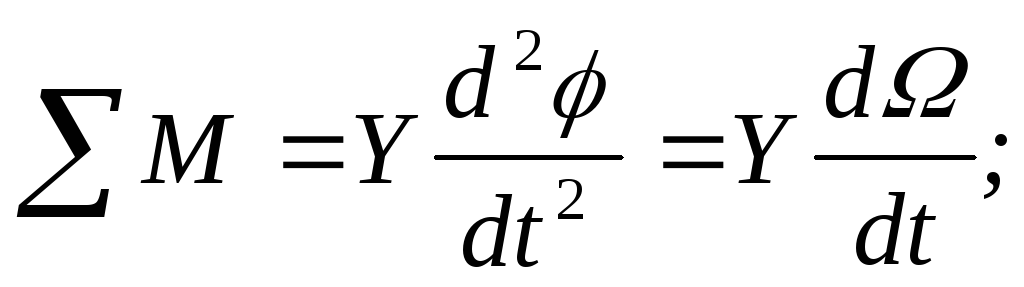ля вращательного:

Y – момент инерции снаряда относительно продольной оси.

 - угловая скорость снаряда.

Y=m_ir_i2=r²dm=m²=(q/g)².

 - радиус инерции.

У равнение вращательного движения:

K

 для прогрессивной крутизны.

_ =0  для постоянной крутизны.

П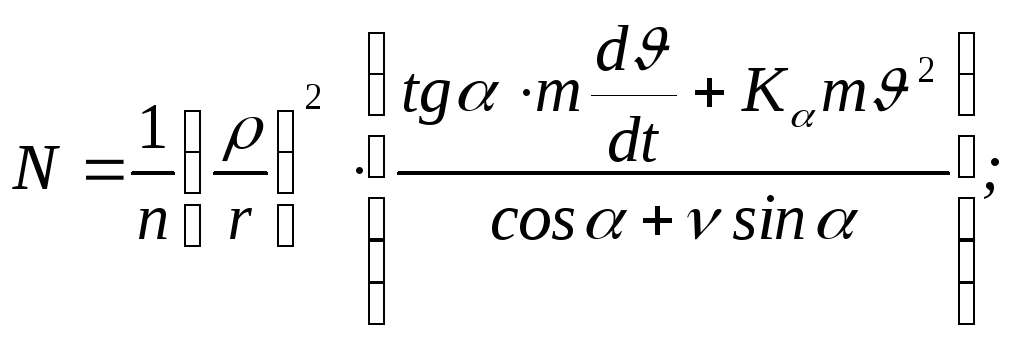 одставим Y и d/dt в формулу получим.

Для определения m(d/dt) – напишем уравнение поступательного движения с учетом сил сопротивления:

P _сн – давление газов на дно снаряда.

n N(sin + cos )=R – сила сопротивления от реакции нарезов.

П одставим в выражение для N получим:

З аметим, что ₁(cos - sin ) 1;

Тогда при k_=const прогрессивная нарезка:

При k_ =0:

(/r)²= - зависит от типа снаряда =0.48 –0.68.

1. нарезка постоянной крутизны.

2. ₁=S⁰; ₂=10⁰.

3. ₁=2⁰; ₂=10⁰.

выше было получено выражение для R:

R=nN(sin  +cos )=nNcos (tg +).

Д ля нарезки постоянной крутизны (cos 1):

В еличина ₁ – так же постоянна.

Введем эту величину в уравнение поступательного движения:

SP_сн=₁m(d/dt); ₁1.02.

Д ля нарезки прогрессивной крутизны:

Примем =1+(R/SP_сн) – varia.

Второстепенные работы ПГ при выстреле.

Р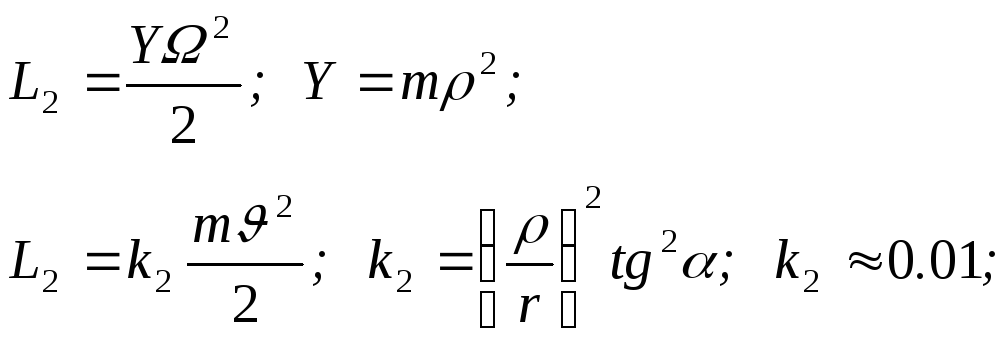 абота, затрачиваемая на вращение снаряда:

Работа, затрачиваемая на преодоление трения в нарезах.

Сумма слагающих сил трения:

n Ncos .

Работа по преодолению этого сопротивления:

dl/cos  - элементарный путь вдоль нареза.

П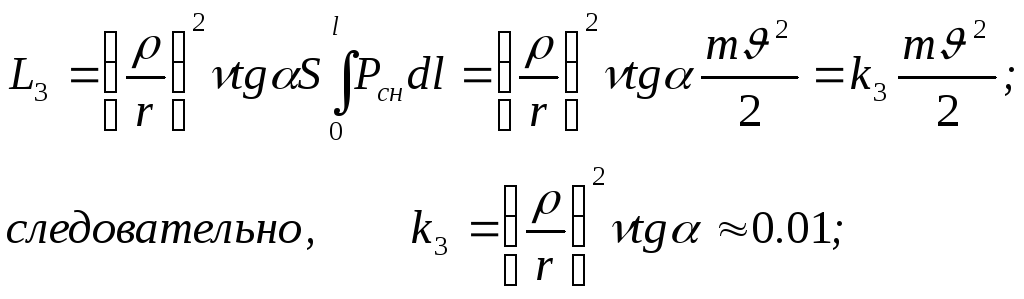 одставим сюда N из уравнения k_ =0:

Работа, затрачиваемая на перемещение газа и заряда.

1. Камора не имеет уширения.

Примем некоторые допущения:

1. Канал, включая камору имеет одну и ту же площадь.

2. При каждом положении снаряда в канале газопороховая смесь распределена равномерно по всему пространству от дна каморы до дна снаряда.

3. Элементы заряда имеют только поступательное движение, причем скорость их от слоя к слою растет линейно от 0 у дна каморы до  у дна снаряда. Ствол принимается неподвижным.

4. С

   

   корости частиц в данном поперечном сечении одинаковы и трение частиц о стенки канала отсутствует.

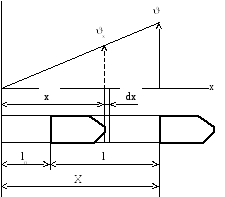
Обозначим  - скорость снаряда. _x – скорость элемента заряда в данном слое. =/g – масса заряда. X – расстояние от дна каморы до дна снаряда. X=l₀+l.

Для данного момента, когда снаряд прошел путь l, X=const.

В ыделим слой сечением S и высотой dx, массой d. Слой имеет скорость _x, его элементарная живая сила.

Для получения всей живой силы надо проинтегрировать по х от 0 до Х.

И з допущения о равномерном распределении масс имеем:

П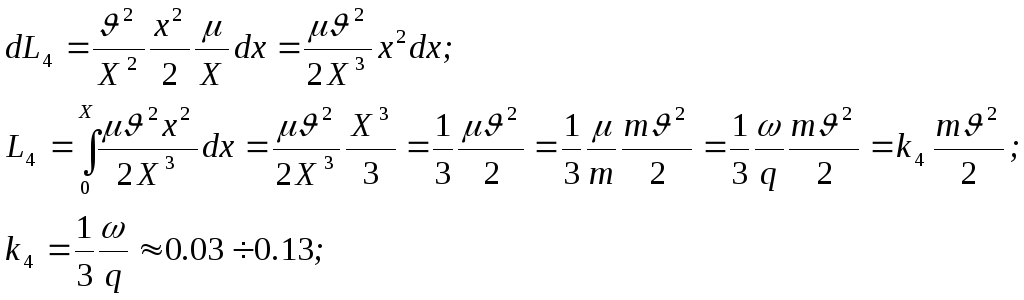 ри допущении, что скорость _х меняется линейно _x/=x/X; _x=(/X)x.

С учетом этого:

2. Камора имеет уширение.

1. Масса газов распределена в заснарядном объеме равномерно, но в движении участвуют не все газы, а лишь по сечению S. Трением пренебрегаем.

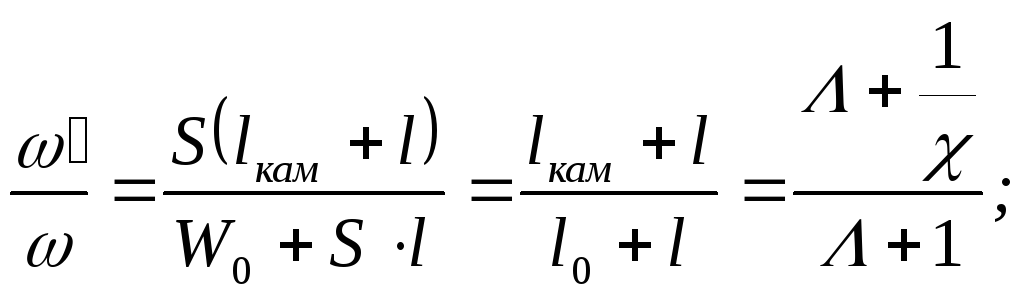2. Закон распределения скорости линейный то 0 у дна каморы до  у дна снаряда. ’ – вес участвующий в движении.

=x₀/l_кам – к-т уширения каморы.

=l/l₀ – относительная длина пути снаряда.

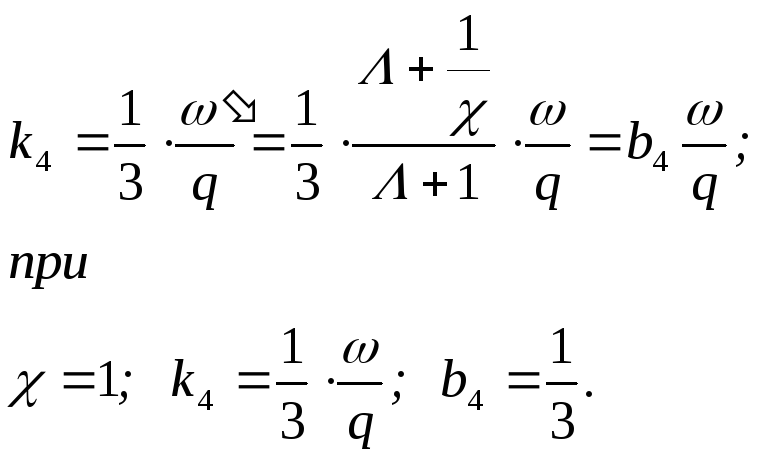
По мере движения снаряда к-т b₄ растет, меняясь от b₄=1/3(1/) при =0 до b₄1/3 при увеличении к-т , т.к.  меняется, то при интегрировании уравнений ВБ приходится б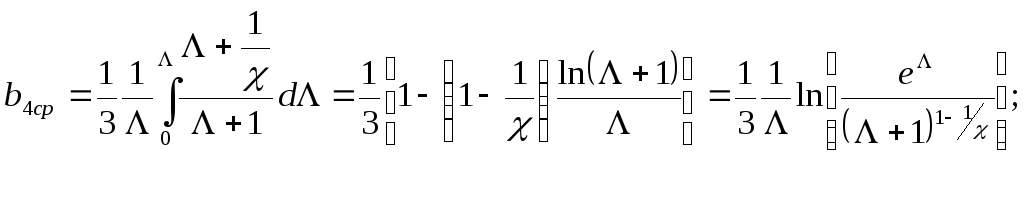 рать b_н в среднем от 0 до _g, где _g=l_g/l₀.

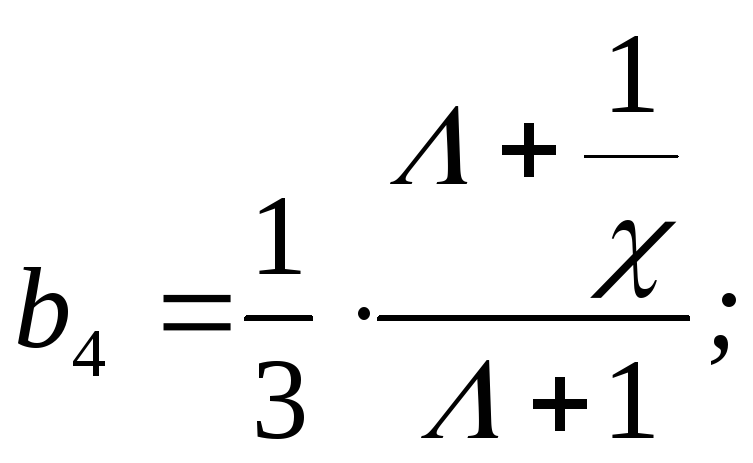Выражение:

М ожно представить в виде:

П озже Бетехтин и Мамонтов дали более точную зависимость:

31