Примечание
Метод решения задач (К01 КМТ(Р) при n>1) по определению перемещений, моментов времени и кинематических параметров для нескольких МТ или одной МТ на различных участках может быть использован и в случаях, если какие-то движения МТ неравномерны или неравнопеременны. В этих случаях также решается система уравнений, которые могут быть получены как из формул схемы алгоритмов К01 КМТ(Р), так и К01 КМТ.
Пример
2 Точка С, выйдя из положения С0 (0, ) (рис.15), где = 2 м, движется по окружности (x – )2 + (y – )2 = 2 равноускоренно против хода часовой стрелки с начальной скоростью V0=3 м/с. В то же время из начала координат вышла другая точка B, которая движется по оси x равноускоренно без начальной скорости.
Рис. 15
Каково должно быть касательное ускорение точки С и ускорение точки B, чтобы в пункт D0 (,0) обе точки пришли одновременно с одинаковыми по модулю и направлению скоростями?
Сколько времени потребуется точкам C и В, чтобы попасть в точку D (2,0), если из точки D0 в точку D они равномерно перемещаются совместно вдоль оси х со скоростью, достигнутой в точке D0?
3 n=3
=1 перемещение точки C из положения Cо в положение D0;
=2 перемещение точки B из положения Bо в положение D0;
=3 перемещение точек C и В совместно из положения D0 в положение D.
=1
4 Криволинейное движение.
5г
Равнопеременное
движение
.
6г
- 8г
Так как для точки C
по условиям задачи
,
,
, то
для точки С в положении D0
получим:
1)
, 2)
.
=2
4 Прямолинейное движение.
5б
Равнопеременное движение
.
6б
- 8б
Так как для точки B
по условию задачи 
,
,
,
то для точки B
в положении D0
получим:
3)
, 4)
.
=3
4 Прямолинейное движение.
5а Равномерное движение V3=const.
6а
- 8а
Так как для точек С и B
по условиям задачи при их совместном
движении из точки D0
в D
,
то для точек С и В в положении D
получим:
5)
.
9
Система пяти уравнений включает в
себя восемь неизвестных:
,
и она имеет вид:
,
Учтя,
что на основании условий задачи: t2=t1,
V2=V1
для двух точек С и B
в положении D0
,
получим cистему
пяти уравнений с пятью неизвестными:
.
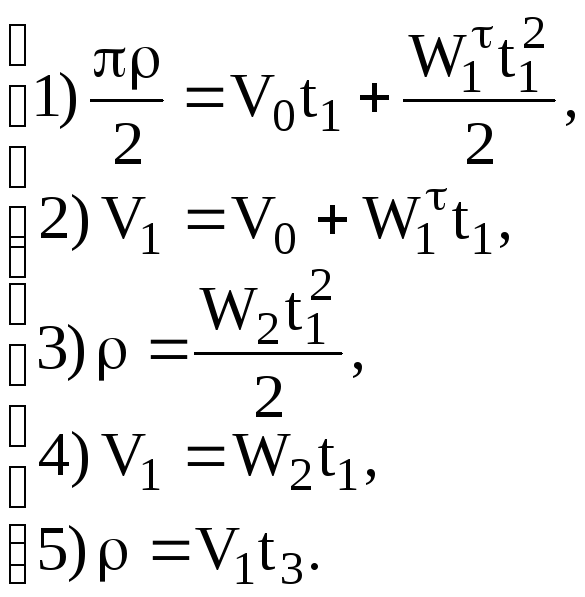
Cистема уравнений 1) — 5) решается путем последовательного исключения неизвестных.
Из уравнений 2) и 3) получим соответственно:
6)
,
7)
.
Уравнения 1) и 4) после подстановки в них соответственно соотношений 6) и 7) примут вид системы двух уравнений с двумя неизвестными V1 и t1:
Подставив соотношение 9) в 8), получим:
,
тогда
из
9)
,
из 7)
,
из
6)
,
из 5)
.
10
Ответ:
,
,
.